PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_ode_ivp_adams_roots_revcom (d02qg)
Purpose
nag_ode_ivp_adams_roots_revcom (d02qg) is a reverse communication function for integrating a non-stiff system of first-order ordinary differential equations using a variable-order variable-step Adams' method. A root-finding facility is provided.
Syntax
[
t,
y,
root,
irevcm,
trvcm,
yrvcm,
yprvcm,
kgrvcm,
rwork,
iwork,
ifail] = d02qg(
t,
y,
tout,
neqg,
irevcm,
grvcm,
kgrvcm,
rwork,
iwork, 'neqf',
neqf)
[
t,
y,
root,
irevcm,
trvcm,
yrvcm,
yprvcm,
kgrvcm,
rwork,
iwork,
ifail] = nag_ode_ivp_adams_roots_revcom(
t,
y,
tout,
neqg,
irevcm,
grvcm,
kgrvcm,
rwork,
iwork, 'neqf',
neqf)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lrwork and liwork were removed from the interface |
Description
Given the initial values
nag_ode_ivp_adams_roots_revcom (d02qg) integrates a non-stiff system of first-order differential equations of the type
from
to
using a variable-order variable-step Adams' method. You define the system by reverse communication, evaluating
in terms of
and
, and
are supplied at
by
nag_ode_ivp_adams_roots_revcom (d02qg). The function is capable of finding roots (values of
) of prescribed event functions of the form
Each
is considered to be independent of the others so that roots are sought of each
individually. The root reported by the function will be the first root encountered by any
. Two techniques for determining the presence of a root in an integration step are available: the sophisticated method described in
Watts (1985) and a simplified method whereby sign changes in each
are looked for at the ends of each integration step. You also define each
by reverse communication. In one-step mode the function returns an approximation to the solution at each integration point. In interval mode this value is returned at the end of the integration range. If a root is detected this approximation is given at the root. You select the mode of operation, the error control, the root-finding technique and various optional inputs by a prior call to the setup function
nag_ode_ivp_adams_setup (d02qw).
For a description of the practical implementation of an Adams' formula see
Shampine and Gordon (1975).
References
Shampine L F and Gordon M K (1975) Computer Solution of Ordinary Differential Equations – The Initial Value Problem W H Freeman & Co., San Francisco
Shampine L F and Watts H A (1979) DEPAC – design of a user oriented package of ODE solvers Report SAND79-2374 Sandia National Laboratory
Watts H A (1985) RDEAM – An Adams ODE code with root solving capability Report SAND85-1595 Sandia National Laboratory
Parameters
Note: this function uses
reverse communication. Its use involves an initial entry, intermediate exits and re-entries, and a final exit, as indicated by the argument
irevcm. Between intermediate exits and re-entries,
all arguments other than grvcm and rwork must remain unchanged.
Compulsory Input Parameters
- 1:
– double scalar
-
On initial entry: that is after a call to
nag_ode_ivp_adams_setup (d02qw) with
,
t must be set to the initial value of the independent variable
.
- 2:
– double array
-
On initial entry: the initial values of the solution .
- 3:
– double scalar
-
On initial entry: the next value of
at which a computed solution is required. For the initial
t, the input value of
tout is used to determine the direction of integration. Integration is permitted in either direction. If
on exit,
tout must be reset beyond
t in the direction of integration, before any continuation call.
- 4:
– int64int32nag_int scalar
-
On initial entry: the number of event functions which you are defining for root-finding. If root-finding is not required the value for
neqg must be
. Otherwise it must be the same value as the argument
neqg used in the prior call to
nag_ode_ivp_adams_setup (d02qw).
- 5:
– int64int32nag_int scalar
-
On initial entry: must have the value .
- 6:
– double scalar
-
On initial entry: need not be set.
On intermediate re-entry: with
,
,
or
,
grvcm must contain the value of
, where
is given by
kgrvcm.
- 7:
– int64int32nag_int scalar
-
On intermediate re-entry: with
,
,
or
,
kgrvcm must remain unchanged from a previous call to
nag_ode_ivp_adams_roots_revcom (d02qg).
- 8:
– double array
-
This
must be the same argument
rwork as supplied to
nag_ode_ivp_adams_setup (d02qw). It is used to pass information from
nag_ode_ivp_adams_setup (d02qw) to
nag_ode_ivp_adams_roots_revcom (d02qg), and from
nag_ode_ivp_adams_roots_revcom (d02qg) to
nag_ode_ivp_adams_diag (d02qx),
nag_ode_ivp_adams_rootdiag (d02qy) and
nag_ode_ivp_adams_interp (d02qz). Therefore the contents of this array
must not be changed before the call to
nag_ode_ivp_adams_roots_revcom (d02qg) or calling any of the functions
nag_ode_ivp_adams_diag (d02qx),
nag_ode_ivp_adams_rootdiag (d02qy) and
nag_ode_ivp_adams_interp (d02qz).
- 9:
– int64int32nag_int array
-
This
must be the same argument
iwork as supplied to
nag_ode_ivp_adams_setup (d02qw). It is used to pass information from
nag_ode_ivp_adams_setup (d02qw) to
nag_ode_ivp_adams_roots_revcom (d02qg), and from
nag_ode_ivp_adams_roots_revcom (d02qg) to
nag_ode_ivp_adams_diag (d02qx),
nag_ode_ivp_adams_rootdiag (d02qy) and
nag_ode_ivp_adams_interp (d02qz). Therefore the contents of this array
must not be changed before the call to
nag_ode_ivp_adams_roots_revcom (d02qg) or calling any of the functions
nag_ode_ivp_adams_diag (d02qx),
nag_ode_ivp_adams_rootdiag (d02qy) and
nag_ode_ivp_adams_interp (d02qz).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
y.
On initial entry: the number of first-order ordinary differential equations to be solved by
nag_ode_ivp_adams_roots_revcom (d02qg). It must contain the same value as the argument
neqf used in the prior call to
nag_ode_ivp_adams_setup (d02qw).
Constraint:
.
Output Parameters
- 1:
– double scalar
-
On final exit: the value of
at which
has been computed. This may be an intermediate output point, a root,
tout or a point at which an error has occurred. If the integration is to be continued, possibly with a new value for
tout,
t must not be changed.
- 2:
– double array
-
On final exit: the computed values of the solution at the exit value of
t. If the integration is to be continued, possibly with a new value for
tout, these values must not be changed.
- 3:
– logical scalar
-
On final exit: if root-finding was required (
on entry), then
root specifies whether or not the output value of the argument
t is a root of one of the event functions. If
, then no root was detected, whereas
indicates a root and you should make a call to
nag_ode_ivp_adams_rootdiag (d02qy) for further information.
If root-finding was not required ( on entry), then .
- 4:
– int64int32nag_int scalar
-
On intermediate exit:
specifies what action you must take before re-entering
nag_ode_ivp_adams_roots_revcom (d02qg) with irevcm unchanged.
- , , , , , or
- Indicates that you must supply , where is given by trvcm and
is returned in , for when and
, for when .
should be placed in location , for .
- Indicates that the current step was not successful due to error test failure. The only information supplied to you on this return is the current value of the independent variable t, as given by trvcm. No values must be changed before re-entering nag_ode_ivp_adams_roots_revcom (d02qg). This facility enables you to determine the number of unsuccessful steps.
- , , or
- Indicates that you must supply , where is given by kgrvcm, is given by trvcm, is given by and is given by . The result should be placed in the variable grvcm.
On final exit: has the value
, which indicates that an output point or root has been reached or an error has occurred (see
ifail).
- 5:
– double scalar
-
On intermediate exit:
the current value of the independent variable.
- 6:
– int64int32nag_int scalar
-
On intermediate exit:
with
,
,
,
,
,
,
,
,
,
or
,
yrvcm specifies the locations of the dependent variables
for use in evaluating the differential system or the event functions.
- is given by , for .
- is given by , for .
- 7:
– int64int32nag_int scalar
-
On intermediate exit:
with
,
,
,
,
,
or
,
yprvcm specifies the positions in
rwork at which you should place the derivatives
.
should be placed in location
, for
.
With
,
,
or
,
yprvcm specifies the locations of the derivatives
for use in evaluating the event functions.
is given by
, for
.
- 8:
– int64int32nag_int scalar
-
On intermediate exit:
with
,
,
or
,
kgrvcm specifies which event function
you must evaluate.
- 9:
– double array
-
- 10:
– int64int32nag_int array
-
- 11:
– int64int32nag_int scalar
On final exit:
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
On entry, the integrator detected an illegal input, or
nag_ode_ivp_adams_setup (d02qw) has not been called before the call to the integrator.
This error may be caused by overwriting elements of
rwork and
iwork.
- W
-
The maximum number of steps has been attempted (at a cost of about
derivative evaluations per step). (See argument
maxstp in
nag_ode_ivp_adams_setup (d02qw).) If integration is to be continued then you need only reset
ifail and call the function again and a further
maxstp steps will be attempted.
-
-
The step size needed to satisfy the error requirements is too small for the
machine precision being used. (See argument
tolfac in
nag_ode_ivp_adams_diag (d02qx).)
- W
-
Some error weight
became zero during the integration (see arguments
vectol,
rtol and
atol in
nag_ode_ivp_adams_setup (d02qw).) Pure relative error control (
) was requested on a variable (the
th) which has now become zero. (See argument
badcmp in
nag_ode_ivp_adams_diag (d02qx).) The integration was successful as far as
t.
- W
-
The problem appears to be stiff (see the
D02 Chapter Introduction for a discussion of the term ‘stiff’). Although it is inefficient to use this integrator to solve stiff problems, integration may be continued by resetting
ifail and calling the function again.
- W
-
A change in sign of an event function has been detected but the root-finding process appears to have converged to a singular point
t rather than a root. Integration may be continued by resetting
ifail and calling the function again.
-
-
The code has detected two successive error exits at the current value of
t and cannot proceed. Check all input variables.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy of integration is determined by the arguments
vectol,
rtol and
atol in a prior call to
nag_ode_ivp_adams_setup (d02qw). Note that only the local error at each step is controlled by these arguments. The error estimates obtained are not strict bounds but are usually reliable over one step. Over a number of steps the overall error may accumulate in various ways, depending on the properties of the differential equation system. The code is designed so that a reduction in the tolerances should lead to an approximately proportional reduction in the error. You are strongly recommended to call
nag_ode_ivp_adams_roots_revcom (d02qg) with more than one set of tolerances and to compare the results obtained to estimate their accuracy.
The accuracy obtained depends on the type of error test used. If the solution oscillates around zero a relative error test should be avoided, whereas if the solution is exponentially increasing an absolute error test should not be used. If different accuracies are required for different components of the solution then a component-wise error test should be used. For a description of the error test see the specifications of the arguments
vectol,
rtol and
atol in the function document for
nag_ode_ivp_adams_setup (d02qw).
The accuracy of any roots located will depend on the accuracy of integration and may also be restricted by the numerical properties of . When evaluating you should try to write the code so that unnecessary cancellation errors will be avoided.
Further Comments
If
nag_ode_ivp_adams_roots_revcom (d02qg) fails with
then the combination of
atol and
rtol may be so small that a solution cannot be obtained, in which case the function should be called again with larger values for
rtol and/or
atol (see
nag_ode_ivp_adams_setup (d02qw)). If the accuracy requested is really needed then you should consider whether there is a more fundamental difficulty. For example:
| (a) |
in the region of a singularity the solution components will usually be of a large magnitude. nag_ode_ivp_adams_roots_revcom (d02qg) could be used in one-step mode to monitor the size of the solution with the aim of trapping the solution before the singularity. In any case numerical integration cannot be continued through a singularity, and analytical treatment may be necessary; |
| (b) |
for ‘stiff’ equations, where the solution contains rapidly decaying components, the function will require a very small step size to preserve stability. This will usually be exhibited by excessive computing time and sometimes an error exit with , but usually an error exit with or . The Adams' methods are not efficient in such cases and you should consider using a function from the Sub-chapter D02M–N. A high proportion of failed steps (see argument nfail in nag_ode_ivp_adams_diag (d02qx)) may indicate stiffness but there may be other reasons for this phenomenon. |
nag_ode_ivp_adams_roots_revcom (d02qg) can be used for producing results at short intervals (for example, for graph plotting); you should set
and
tcrit to the last output point required in a prior call to
nag_ode_ivp_adams_setup (d02qw) and then set
tout appropriately for each output point in turn in the call to
nag_ode_ivp_adams_roots_revcom (d02qg)Example
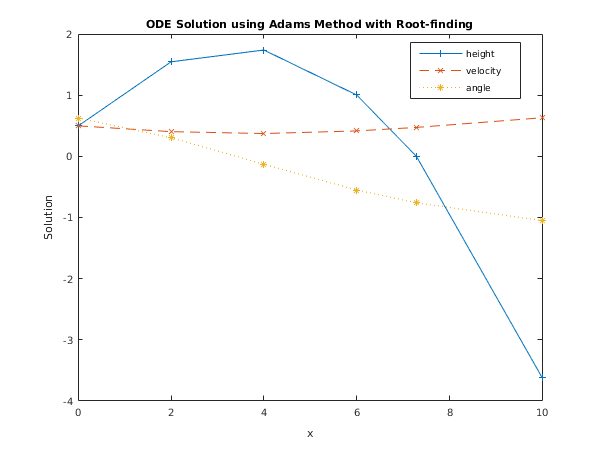
This example solves the following system (for a projectile)
over an interval
starting with values
,
and
using scalar error control (
) until the first point where
is encountered.
Also, nag_ode_ivp_adams_roots_revcom (d02qg) is used to produce output at intervals of .
Open in the MATLAB editor:
d02qg_example
function d02qg_example
fprintf('d02qg example results\n\n');
statef = 'S';
neqf = int64(3);
vectol = false;
atol = [1e-4];
rtol = [1e-7];
onestp = false;
crit = true;
tcrit = 10;
hmax = 2;
maxstp = int64(500);
neqg = int64(1);
alterg = false;
sophst = true;
rwork = zeros(106, 1);
iwork = zeros(25, 1, 'int64');
[statef, alterg, rwork, iwork, ifail] = ...
d02qw(...
statef, neqf, vectol, atol, rtol, onestp, crit, tcrit, ...
hmax, maxstp, neqg, alterg, sophst, rwork, iwork);
%Initialize integrator input variables
t = 0;
y = [0.5; 0.5; 0.2*pi];
grv = 0;
kgrv = int64(0);
tinc = 2;
ncall = 1;
tkeep = zeros(1,1);
ykeep = zeros(1,neqf);
fprintf(' t y(1) y(2) y(3)\n');
fprintf('%7.4f %7.4f %7.4f %7.4f\n', t, y(1), y(2), y(3));
tkeep(ncall) = t;
ykeep(ncall,:) = y;
for j=1:5
tout = double(j)*tinc;
irevcm = int64(0);
first_call = true;
while (irevcm ~= 0 || first_call)
first_call = false;
[t, y, root, irevcm, trv, yrv, yprv, kgrv, rwork, iwork, ifail] = ...
d02qg(...
t, y, tout, neqg, irevcm, grv, kgrv, rwork, iwork);
if (irevcm > 0 && irevcm < 8)
if (yrv == 0)
rwork(yprv) = tan(y(3));
rwork(yprv+1) = -0.032*tan(y(3))/y(2) - 0.02*y(2)/cos(y(3));
rwork(yprv+2) = -0.032/y(2)^2;
else
y2 = rwork(yrv+1);
y3 = rwork(yrv+2);
rwork(yprv) = tan(y3);
rwork(yprv+1) = -0.032*tan(y3)/y2 - 0.02*y2/cos(y3);
rwork(yprv+2) = -0.032/y2^2;
end
elseif (irevcm > 8)
grv = y(1);
end
end
fprintf('%7.4f %7.4f %7.4f %7.4f\n', t, y(1), y(2), y(3));
ncall = ncall + 1;
tkeep(ncall) = t;
ykeep(ncall,:) = y;
end
fig1 = figure;
display_plot(tkeep, ykeep)
function display_plot(tkeep, ykeep)
plot(tkeep, ykeep(:,1), '-+', tkeep, ykeep(:,2), '--x', tkeep, ...
ykeep(:,3), ':*');
%Add title.
title('ODE Solution using Adams Method with Root-finding');
xlabel('x');
ylabel('Solution');
legend('height','velocity','angle','Location','Best');
d02qg example results
t y(1) y(2) y(3)
0.0000 0.5000 0.5000 0.6283
2.0000 1.5493 0.4055 0.3066
4.0000 1.7424 0.3743 -0.1289
6.0000 1.0058 0.4173 -0.5507
7.2879 -0.0000 0.4749 -0.7601
10.0000 -3.6287 0.6333 -1.0515
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015