PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_1d_parab_convdiff (d03pf)
Purpose
nag_pde_1d_parab_convdiff (d03pf) integrates a system of linear or nonlinear convection-diffusion equations in one space dimension, with optional source terms. The system must be posed in conservative form. Convection terms are discretized using a sophisticated upwind scheme involving a user-supplied numerical flux function based on the solution of a Riemann problem at each mesh point. The method of lines is employed to reduce the PDEs to a system of ordinary differential equations (ODEs), and the resulting system is solved using a backward differentiation formula (BDF) method.
Syntax
[
ts,
u,
rsave,
isave,
ind,
ifail] = d03pf(
ts,
tout,
pdedef,
numflx,
bndary,
u,
x,
acc,
tsmax,
rsave,
isave,
itask,
itrace,
ind, 'npde',
npde, 'npts',
npts)
[
ts,
u,
rsave,
isave,
ind,
ifail] = nag_pde_1d_parab_convdiff(
ts,
tout,
pdedef,
numflx,
bndary,
u,
x,
acc,
tsmax,
rsave,
isave,
itask,
itrace,
ind, 'npde',
npde, 'npts',
npts)
Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lrsave and lisave were removed from the interface |
Description
nag_pde_1d_parab_convdiff (d03pf) integrates the system of convection-diffusion equations in conservative form:
or the hyperbolic convection-only system:
for
, where the vector
is the set of solution values
The functions
,
,
and
depend on
,
and
; and
depends on
,
,
and
, where
is the spatial derivative of
. Note that
,
,
and
must not depend on any space derivatives; and none of the functions may depend on time derivatives. In terms of conservation laws,
,
and
are the convective flux, diffusion and source terms respectively.
The integration in time is from to , over the space interval , where and are the leftmost and rightmost points of a user-defined mesh . The initial values of the functions must be given at .
The PDEs are approximated by a system of ODEs in time for the values of
at mesh points using a spatial discretization method similar to the central-difference scheme used in
nag_pde_1d_parab_fd (d03pc),
nag_pde_1d_parab_dae_fd (d03ph) and
nag_pde_1d_parab_remesh_fd (d03pp), but with the flux
replaced by a
numerical flux, which is a representation of the flux taking into account the direction of the flow of information at that point (i.e., the direction of the characteristics). Simple central differencing of the numerical flux then becomes a sophisticated upwind scheme in which the correct direction of upwinding is automatically achieved.
The numerical flux vector,
say, must be calculated by you in terms of the
left and
right values of the solution vector
(denoted by
and
respectively), at each mid-point of the mesh
, for
. The left and right values are calculated by
nag_pde_1d_parab_convdiff (d03pf) from two adjacent mesh points using a standard upwind technique combined with a Van Leer slope-limiter (see
LeVeque (1990)). The physically correct value for
is derived from the solution of the Riemann problem given by
where
, i.e.,
corresponds to
, with discontinuous initial values
for
and
for
, using an
approximate Riemann solver. This applies for either of the systems
(1) or
(2); the numerical flux is independent of the functions
,
,
and
. A description of several approximate Riemann solvers can be found in
LeVeque (1990) and
Berzins et al. (1989). Roe's scheme (see
Roe (1981)) is perhaps the easiest to understand and use, and a brief summary follows. Consider the system of PDEs
or equivalently
. Provided the system is linear in
, i.e., the Jacobian matrix
does not depend on
, the numerical flux
is given by
where
(
) is the flux
calculated at the left (right) value of
, denoted by
(
); the
are the eigenvalues of
; the
are the right eigenvectors of
; and the
are defined by
An example is given in
Example.
If the system is nonlinear, Roe's scheme requires that a linearized Jacobian is found (see
Roe (1981)).
The functions
,
,
and
(but
not
) must be specified in a
pdedef. The numerical flux
must be supplied in a separate
numflx. For problems in the form
(2), the actual argument
nag_pde_1d_parab_convdiff_sample_pdedef (d03pfp) may be used for
pdedef.
nag_pde_1d_parab_convdiff_sample_pdedef (d03pfp) is included in the NAG Toolbox and sets the matrix with entries
to the identity matrix, and the functions
,
and
to zero.
The boundary condition specification has sufficient flexibility to allow for different types of problems. For second-order problems, i.e.,
depending on
, a boundary condition is required for each PDE at both boundaries for the problem to be well-posed. If there are no second-order terms present, then the continuous PDE problem generally requires exactly one boundary condition for each PDE, that is
npde boundary conditions in total. However, in common with most discretization schemes for first-order problems, a
numerical boundary condition is required at the other boundary for each PDE. In order to be consistent with the characteristic directions of the PDE system, the numerical boundary conditions must be derived from the solution inside the domain in some manner (see below). You must supply both types of boundary conditions, i.e., a total of
npde conditions at each boundary point.
The position of each boundary condition should be chosen with care. In simple terms, if information is flowing into the domain then a physical boundary condition is required at that boundary, and a numerical boundary condition is required at the other boundary. In many cases the boundary conditions are simple, e.g., for the linear advection equation. In general you should calculate the characteristics of the PDE system and specify a physical boundary condition for each of the characteristic variables associated with incoming characteristics, and a numerical boundary condition for each outgoing characteristic.
A common way of providing numerical boundary conditions is to extrapolate the characteristic variables from the inside of the domain. Note that only linear extrapolation is allowed in this function (for greater flexibility the function
nag_pde_1d_parab_convdiff_dae (d03pl) should be used). For problems in which the solution is known to be uniform (in space) towards a boundary during the period of integration then extrapolation is unnecessary; the numerical boundary condition can be supplied as the known solution at the boundary. Examples can be found in
Example.
The boundary conditions must be specified in
bndary in the form
at the left-hand boundary, and
at the right-hand boundary.
Note that spatial derivatives at the boundary are not passed explicitly to
bndary, but they can be calculated using values of
at and adjacent to the boundaries if required. However, it should be noted that instabilities may occur if such one-sided differencing opposes the characteristic direction at the boundary.
The problem is subject to the following restrictions:
| (i) |
, , and must not depend on any space derivatives; |
| (ii) |
, , , and must not depend on any time derivatives; |
| (iii) |
, so that integration is in the forward direction; |
| (iv) |
The evaluation of the terms , , and is done by calling the pdedef at a point approximately midway between each pair of mesh points in turn. Any discontinuities in these functions must therefore be at one or more of the mesh points ; |
| (v) |
At least one of the functions must be nonzero so that there is a time derivative present in the PDE problem. |
In total there are ODEs in the time direction. This system is then integrated forwards in time using a BDF method.
For further details of the algorithm, see
Pennington and Berzins (1994) and the references therein.
References
Berzins M, Dew P M and Furzeland R M (1989) Developing software for time-dependent problems using the method of lines and differential-algebraic integrators Appl. Numer. Math. 5 375–397
Hirsch C (1990) Numerical Computation of Internal and External Flows, Volume 2: Computational Methods for Inviscid and Viscous Flows John Wiley
LeVeque R J (1990) Numerical Methods for Conservation Laws Birkhäuser Verlag
Pennington S V and Berzins M (1994) New NAG Library software for first-order partial differential equations ACM Trans. Math. Softw. 20 63–99
Roe P L (1981) Approximate Riemann solvers, parameter vectors, and difference schemes J. Comput. Phys. 43 357–372
Parameters
Compulsory Input Parameters
- 1:
– double scalar
-
The initial value of the independent variable .
Constraint:
.
- 2:
– double scalar
-
The final value of to which the integration is to be carried out.
- 3:
– function handle or string containing name of m-file
-
pdedef must evaluate the functions
,
,
and
which partially define the system of PDEs.
,
and
may depend on
,
and
;
may depend on
,
,
and
.
pdedef is called approximately midway between each pair of mesh points in turn by
nag_pde_1d_parab_convdiff (d03pf). The actual argument
nag_pde_1d_parab_convdiff_sample_pdedef (d03pfp) may be used for
pdedef for problems in the form
(2). (
nag_pde_1d_parab_convdiff_sample_pdedef (d03pfp) is included in the NAG Toolbox.)
[p, c, d, s, ires] = pdedef(npde, t, x, u, ux, ires)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 2:
– double scalar
-
The current value of the independent variable .
- 3:
– double scalar
-
The current value of the space variable .
- 4:
– double array
-
contains the value of the component , for .
- 5:
– double array
-
contains the value of the component , for .
- 6:
– int64int32nag_int scalar
-
Set to .
Output Parameters
- 1:
– double array
-
must be set to the value of , for and .
- 2:
– double array
-
must be set to the value of , for .
- 3:
– double array
-
must be set to the value of , for .
- 4:
– double array
-
must be set to the value of , for .
- 5:
– int64int32nag_int scalar
-
Should usually remain unchanged. However, you may set
ires to force the integration function to take certain actions as described below:
- Indicates to the integrator that control should be passed back immediately to the calling function with the error indicator set to .
- Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set when a physically meaningless input or output value has been generated. If you consecutively set , then nag_pde_1d_parab_convdiff (d03pf) returns to the calling function with the error indicator set to .
- 4:
– function handle or string containing name of m-file
-
numflx must supply the numerical flux for each PDE given the
left and
right values of the solution vector
.
numflx is called approximately midway between each pair of mesh points in turn by
nag_pde_1d_parab_convdiff (d03pf).
[flux, ires] = numflx(npde, t, x, uleft, uright, ires)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 2:
– double scalar
-
The current value of the independent variable .
- 3:
– double scalar
-
The current value of the space variable .
- 4:
– double array
-
contains the left value of the component , for .
- 5:
– double array
-
contains the right value of the component , for .
- 6:
– int64int32nag_int scalar
-
Set to .
Output Parameters
- 1:
– double array
-
must be set to the numerical flux , for .
- 2:
– int64int32nag_int scalar
-
Should usually remain unchanged. However, you may set
ires to force the integration function to take certain actions as described below:
- Indicates to the integrator that control should be passed back immediately to the calling function with the error indicator set to .
- Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set when a physically meaningless input or output value has been generated. If you consecutively set , then nag_pde_1d_parab_convdiff (d03pf) returns to the calling function with the error indicator set to .
- 5:
– function handle or string containing name of m-file
-
bndary must evaluate the functions
and
which describe the physical and numerical boundary conditions, as given by
(6) and
(7).
[g, ires] = bndary(npde, npts, t, x, u, ibnd, ires)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of PDEs in the system.
- 2:
– int64int32nag_int scalar
-
The number of mesh points in the interval .
- 3:
– double scalar
-
The current value of the independent variable .
- 4:
– double array
-
The mesh points in the spatial direction. corresponds to the left-hand boundary, , and corresponds to the right-hand boundary, .
- 5:
– double array
-
Contains the value of solution components in the boundary region.
If , contains the value of the component at , for and .
If , contains the value of the component at , for and .
- 6:
– int64int32nag_int scalar
-
Specifies which boundary conditions are to be evaluated.
- bndary must evaluate the left-hand boundary condition at .
- bndary must evaluate the right-hand boundary condition at .
- 7:
– int64int32nag_int scalar
-
Set to .
Output Parameters
- 1:
– double array
-
must contain the
th component of either
or
in
(6) and
(7), depending on the value of
ibnd, for
.
- 2:
– int64int32nag_int scalar
-
Should usually remain unchanged. However, you may set
ires to force the integration function to take certain actions as described below:
- Indicates to the integrator that control should be passed back immediately to the calling function with the error indicator set to .
- Indicates to the integrator that the current time step should be abandoned and a smaller time step used instead. You may wish to set when a physically meaningless input or output value has been generated. If you consecutively set , then nag_pde_1d_parab_convdiff (d03pf) returns to the calling function with the error indicator set to .
- 6:
– double array
-
must contain the initial value of at and , for and .
- 7:
– double array
-
The mesh points in the space direction. must specify the left-hand boundary, , and must specify the right-hand boundary, .
Constraint:
.
- 8:
– double array
-
The components of
acc contain the relative and absolute error tolerances used in the local error test in the time integration.
If
is the estimated error for
at the
th mesh point, the error test is
Constraint:
and (but not both zero).
- 9:
– double scalar
-
The maximum absolute step size to be allowed in the time integration. If then no maximum is imposed.
Constraint:
.
- 10:
– double array
-
lrsave, the dimension of the array, must satisfy the constraint
.
If
,
rsave need not be set on entry.
If
,
rsave must be unchanged from the previous call to the function because it contains required information about the iteration.
- 11:
– int64int32nag_int array
-
lisave, the dimension of the array, must satisfy the constraint
.
If
,
isave need not be set on entry.
If
,
isave must be unchanged from the previous call to the function because it contains required information about the iteration. In particular:
- Contains the number of steps taken in time.
- Contains the number of residual evaluations of the resulting ODE system used. One such evaluation involves computing the PDE functions at all the mesh points, as well as one evaluation of the functions in the boundary conditions.
- Contains the number of Jacobian evaluations performed by the time integrator.
- Contains the order of the last backward differentiation formula method used.
- Contains the number of Newton iterations performed by the time integrator. Each iteration involves an ODE residual evaluation followed by a back-substitution using the decomposition of the Jacobian matrix.
- 12:
– int64int32nag_int scalar
-
The task to be performed by the ODE integrator.
- Normal computation of output values at (by overshooting and interpolating).
- Take one step in the time direction and return.
- Stop at first internal integration point at or beyond .
Constraint:
, or .
- 13:
– int64int32nag_int scalar
-
The level of trace information required from
nag_pde_1d_parab_convdiff (d03pf) and the underlying ODE solver.
itrace may take the value
,
,
,
or
.
- No output is generated.
- Only warning messages from the PDE solver are printed on the current error message unit (see nag_file_set_unit_error (x04aa)).
- Output from the underlying ODE solver is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)). This output contains details of Jacobian entries, the nonlinear iteration and the time integration during the computation of the ODE system.
If , then is assumed and similarly if , then is assumed.
The advisory messages are given in greater detail as
itrace increases. You are advised to set
, unless you are experienced with
Sub-chapter D02M–N.
- 14:
– int64int32nag_int scalar
-
Indicates whether this is a continuation call or a new integration.
- Starts or restarts the integration in time.
- Continues the integration after an earlier exit from the function. In this case, only the arguments tout and ifail should be reset between calls to nag_pde_1d_parab_convdiff (d03pf).
Constraint:
or .
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the first dimension of the array
u.
The number of PDEs to be solved.
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
x and the second dimension of the array
u. (An error is raised if these dimensions are not equal.)
The number of mesh points in the interval .
Constraint:
.
Output Parameters
- 1:
– double scalar
-
The value of
corresponding to the solution values in
u. Normally
.
- 2:
– double array
-
will contain the computed solution at and , for and .
- 3:
– double array
-
If
,
rsave must be unchanged from the previous call to the function because it contains required information about the iteration.
- 4:
– int64int32nag_int array
-
If
,
isave must be unchanged from the previous call to the function because it contains required information about the iteration. In particular:
- Contains the number of steps taken in time.
- Contains the number of residual evaluations of the resulting ODE system used. One such evaluation involves computing the PDE functions at all the mesh points, as well as one evaluation of the functions in the boundary conditions.
- Contains the number of Jacobian evaluations performed by the time integrator.
- Contains the order of the last backward differentiation formula method used.
- Contains the number of Newton iterations performed by the time integrator. Each iteration involves an ODE residual evaluation followed by a back-substitution using the decomposition of the Jacobian matrix.
- 5:
– int64int32nag_int scalar
-
.
- 6:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | is too small, |
| or | , or , |
| or | , |
| or | , |
| or | or , |
| or | incorrect user-defined mesh, i.e., for some , |
| or | lrsave or lisave are too small, |
| or | on initial entry to nag_pde_1d_parab_convdiff (d03pf), |
| or | or , |
| or | or are both zero, |
| or | . |
- W
-
The underlying ODE solver cannot make any further progress, with the values of
acc, across the integration range from the current point
. The components of
u contain the computed values at the current point
.
- W
-
In the underlying ODE solver, there were repeated error test failures on an attempted step, before completing the requested task, but the integration was successful as far as . The problem may have a singularity, or the error requirement may be inappropriate. Incorrect specification of boundary conditions may also result in this error.
-
-
In setting up the ODE system, the internal initialization function was unable to initialize the derivative of the ODE system. This could be due to the fact that
ires was repeatedly set to
in one of
pdedef,
numflx or
bndary when the residual in the underlying ODE solver was being evaluated. Incorrect specification of boundary conditions may also result in this error.
-
-
In solving the ODE system, a singular Jacobian has been encountered. Check the problem formulation.
- W
-
When evaluating the residual in solving the ODE system,
ires was set to
in at least one of
pdedef,
numflx or
bndary. Integration was successful as far as
.
-
-
The values of and are so small that the function is unable to start the integration in time.
-
-
In either,
pdedef,
numflx or
bndary,
ires was set to an invalid value.
- (nag_ode_ivp_stiff_imp_revcom (d02nn))
-
A serious error has occurred in an internal call to the specified function. Check the problem specification and all arguments and array dimensions. Setting
may provide more information. If the problem persists, contact
NAG.
- W
-
The required task has been completed, but it is estimated that a small change in the values of
acc is unlikely to produce any change in the computed solution. (Only applies when you are not operating in one step mode, that is when
.)
-
-
An error occurred during Jacobian formulation of the ODE system (a more detailed error description may be directed to the current advisory message unit when ).
-
-
Not applicable.
-
-
Not applicable.
-
-
One or more of the functions , or was detected as depending on time derivatives, which is not permissible.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
nag_pde_1d_parab_convdiff (d03pf) controls the accuracy of the integration in the time direction but not the accuracy of the approximation in space. The spatial accuracy depends on both the number of mesh points and on their distribution in space. In the time integration only the local error over a single step is controlled and so the accuracy over a number of steps cannot be guaranteed. You should therefore test the effect of varying the components of the accuracy argument,
acc.
Further Comments
nag_pde_1d_parab_convdiff (d03pf) is designed to solve systems of PDEs in conservative form, with optional source terms which are independent of space derivatives, and optional second-order diffusion terms. The use of the function to solve systems which are not naturally in this form is discouraged, and you are advised to use one of the central-difference schemes for such problems.
You should be aware of the stability limitations for hyperbolic PDEs. For most problems with small error tolerances the ODE integrator does not attempt unstable time steps, but in some cases a maximum time step should be imposed using
tsmax. It is worth experimenting with this argument, particularly if the integration appears to progress unrealistically fast (with large time steps). Setting the maximum time step to the minimum mesh size is a safe measure, although in some cases this may be too restrictive.
Problems with source terms should be treated with caution, as it is known that for large source terms stable and reasonable looking solutions can be obtained which are in fact incorrect, exhibiting non-physical speeds of propagation of discontinuities (typically one spatial mesh point per time step). It is essential to employ a very fine mesh for problems with source terms and discontinuities, and to check for non-physical propagation speeds by comparing results for different mesh sizes. Further details and an example can be found in
Pennington and Berzins (1994).
The time taken depends on the complexity of the system and on the accuracy requested.
Example
For this function two examples are presented. There is a single example program for nag_pde_1d_parab_convdiff (d03pf), with a main program and the code to solve the two example problems given in Example 1 (EX1) and Example 2 (EX2).
Example 1 (EX1)
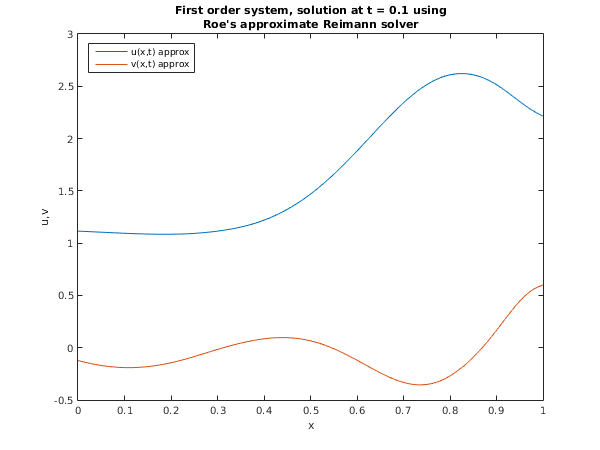
This example is a simple first-order system which illustrates the calculation of the numerical flux using Roe's approximate Riemann solver, and the specification of numerical boundary conditions using extrapolated characteristic variables. The PDEs are
for
and
. The PDEs have an exact solution given by
The initial conditions are given by the exact solution. The characteristic variables are
and
corresponding to the characteristics given by
and
respectively. Hence a physical boundary condition is required for
at the left-hand boundary, and for
at the right-hand boundary (corresponding to the incoming characteristics); and a numerical boundary condition is required for
at the left-hand boundary, and for
at the right-hand boundary (outgoing characteristics). The physical boundary conditions are obtained from the exact solution, and the numerical boundary conditions are calculated by linear extrapolation of the appropriate characteristic variable. The numerical flux is calculated using Roe's approximate Riemann solver: Using the notation in
Description, the flux vector
and the Jacobian matrix
are
and the eigenvalues of
are
and
with right eigenvectors
and
respectively. Using equation
(4) the
are given by
that is
is given by
and similarly for
. From equation
(4), the numerical flux vector is
that is
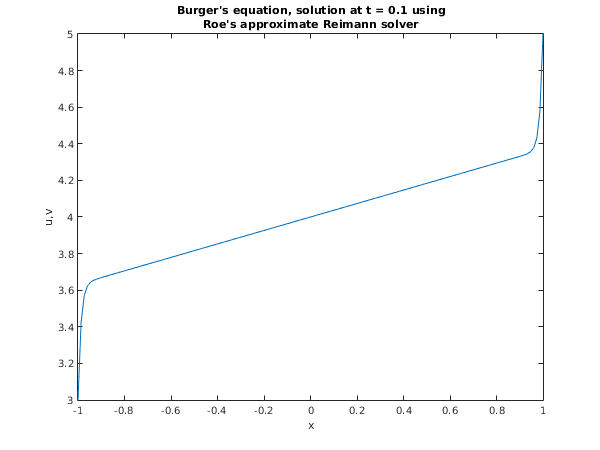
Example 2 (EX2)
This example is an advection-diffusion equation in which the flux term depends explicitly on
:
for
and
. The argument
is taken to be
. The two physical boundary conditions are
and
and the initial condition is
. The integration is run to steady state at which the solution is known to be
across the domain with a narrow boundary layer at both boundaries. In order to write the PDE in conservative form, a source term must be introduced, i.e.,
As in Example 1, the numerical flux is calculated using the Roe approximate Riemann solver. The Riemann problem to solve locally is
The
in the flux term is assumed to be constant at a local level, and so using the notation in
Description,
and
. The eigenvalue is
and the eigenvector (a scalar in this case) is
. The numerical flux is therefore
Open in the MATLAB editor:
d03pf_example
function d03pf_example
fprintf('d03pf example results\n\n');
fprintf('Example 1\n');
ex1;
fprintf('\n\nExample 2\n');
ex2;
function ex1
ts = 0;
tout = 0.1;
npde = 2;
npts = 101;
x = [0:0.01:1];
u = exact(ts,npde,x,npts);
acc = [1e-04; 1e-05];
tsmax = 0;
rsave = zeros(6695, 1);
isave = zeros(226, 1, 'int64');
itask = int64(1);
itrace = int64(0);
ind = int64(0);
[ts, u, rsave, isave, ind, ifail] = ...
d03pf( ...
ts, tout, @pdedef, @numflx1, @bndary1, u, x, acc, ...
tsmax, rsave, isave, itask, itrace, ind);
uerr = exact(ts,npde,x,npts) - u;
l2err = norm(uerr);
fprintf(' At t = %7.4f the L2-error in computed solution = %7.4f\n', ...
ts, l2err);
nsteps = 5*((isave(1)+2)/5);
nfuncs = 50*((isave(2)+25)/50);
njacs = 10*((isave(3)+5)/10);
niters = 50*((isave(5)+25)/50);
fprintf('\n Number of time steps (nearest 5) = %6d\n',nsteps);
fprintf(' Number of function evaluations (nearest 50) = %6d\n',nfuncs);
fprintf(' Number of Jacobian evaluations (neaerst 10) = %6d\n',njacs);
fprintf(' Number of iterations (nearest 50) = %6d\n',niters);
fig1 = figure;
plot(x,u(1,:),x,u(2,:));
title({['First order system, solution at t = 0.1 using'],...
['Roe''s approximate Reimann solver']});
xlabel('x');
ylabel('u,v');
legend('u(x,t) approx','v(x,t) approx','Location','NorthWest');
function ex2
ts = 0;
tout = 1;
npde = 1;
npts = 151;
dx = 2/(npts-1);
x = [-1:dx:1];
u(1,:) = x + 4;
acc = [1e-05; 1e-05];
tsmax = 0.02;
rsave = zeros(6695, 1);
isave = zeros(1000, 1, 'int64');
itask = int64(1);
itrace = int64(0);
ind = int64(0);
[ts, u, rsave, isave, ind, ifail] = ...
d03pf( ...
ts, tout, @pdedef, @numflx2, @bndary2, u, x, acc, ...
tsmax, rsave, isave, itask, itrace, ind);
nsteps = 5*((isave(1)+2)/5);
nfuncs = 50*((isave(2)+25)/50);
njacs = 10*((isave(3)+5)/10);
niters = 50*((isave(5)+25)/50);
fprintf('\n Number of time steps (nearest 5) = %6d\n',nsteps);
fprintf(' Number of function evaluations (nearest 50) = %6d\n',nfuncs);
fprintf(' Number of Jacobian evaluations (neaerst 10) = %6d\n',njacs);
fprintf(' Number of iterations (nearest 50) = %6d\n',niters);
fig2 = figure;
plot(x,u(1,:));
title({['Burger''s equation, solution at t = 0.1 using'],...
['Roe''s approximate Reimann solver']});
xlabel('x');
ylabel('u,v');
function [p, c, d, s, ires] = pdedef(npde, t, x, u, ux, ires)
p = eye(npde);
c = zeros(npde, 1); d = c; s = c;
c(1) = 0.01;
d(1) = ux(1);
s(1) = u(1);
function [flux,ires] = numflx1(npde, t, x, uleft, uright, ires)
flux = zeros(npde,1);
flux(1) = (-2*uright(1)+6*uleft(1)+uright(2)+3*uleft(2))/4;
flux(2) = ( 2*uright(1)+6*uleft(1)-uright(2)+3*uleft(2))/2;
function [flux,ires] = numflx2(npde, t, x, uleft, uright, ires)
if (x>=0)
flux(1) = x*uleft(1);
else
flux(1) = x*uright(1);
end
function [g, ires] = bndary1(npde, npts, t, x, u, ibnd, ires)
np1 = npts-1;
np2 = npts-2;
g = zeros(npde,1);
if (ibnd == 0)
ue = exact(t,npde,x(1),1);
c = (x(2)-x(1))/(x(3)-x(2));
exu1 = (1+c)*u(1,2) - c*u(1,3);
exu2 = (1+c)*u(2,2) - c*u(2,3);
g(1) = 2*u(1,1) + u(2,1) - 2*ue(1,1) - ue(2,1);
g(2) = 2*u(1,1) - u(2,1) - 2*exu1 + exu2;
else
ue = exact(t,npde,x(npts),1);
c = (x(npts)-x(np1))/(x(np1)-x(np2));
exu1 = (1+c)*u(1,2) - c*u(1,3);
exu2 = (1+c)*u(2,2) - c*u(2,3);
g(1) = 2*u(1,1) - u(2,1) - 2*ue(1,1) + ue(2,1);
g(2) = 2*u(1,1) + u(2,1) - 2*exu1 - exu2;
end
function [g, ires] = bndary2(npde, npts, t, x, u, ibnd, ires)
np1 = npts-1;
np2 = npts-2;
g = zeros(npde,1);
if (ibnd == 0)
g(1) = u(1,1) - 3;
else
g(1) = u(1,1) - 5;
end
function u = exact(t,npde,x,npts)
u = zeros(npde,npts);
for i = 1:double(npts)
x1 = x(i) + t;
x2 = x(i) - 3*t;
s1 = sin(2*pi*x1^2)/2;
s2 = sin(2*pi*x2^2)/2;
u(1,i) = (exp(x1)+exp(x2))/2 + (s2-s1)/2 + 2*t^2 - 2*x(i)*t;
u(2,i) = exp(x2)-exp(x1) + (s2+s1) + x(i)^2 + 5*t^2 - 2*x(i)*t;
end
d03pf example results
Example 1
At t = 0.1000 the L2-error in computed solution = 1.5889
Number of time steps (nearest 5) = 35
Number of function evaluations (nearest 50) = 200
Number of Jacobian evaluations (neaerst 10) = 10
Number of iterations (nearest 50) = 100
Example 2
Number of time steps (nearest 5) = 55
Number of function evaluations (nearest 50) = 200
Number of Jacobian evaluations (neaerst 10) = 10
Number of iterations (nearest 50) = 150
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015