public static double s20ad(
	double x
)

Public Shared Function s20ad ( _
	x As Double _
) As Double

public:
static double s20ad(
	double x
)

static member s20ad : 
        x : float -> float 

s20ad returns a value for the Fresnel integral $C\left(x\right)$.

s20ad evaluates an approximation to the Fresnel integral Note:  $C\left(x\right)=-C\left(-x\right)$, so the approximation need only consider $x\ge 0.0$.

The method is based on three Chebyshev expansions:

For $0<x\le 3$, For $x>3$, where $f\left(x\right)={\displaystyle \underset{r=0}{{\sum }^{\prime }}}{b}_r{T}_r\left(t\right)$,

and $g\left(x\right)={\displaystyle \underset{r=0}{{\sum }^{\prime }}}{c}_r{T}_r\left(t\right)$,

with $t=2{\left(\frac{3}{x}\right)}^4-1$.

For small $x$, $C\left(x\right)\simeq x$. This approximation is used when $x$ is sufficiently small for the result to be correct to machine precision.

For large $x$, $f\left(x\right)\simeq \frac{1}{\pi }$ and $g\left(x\right)\simeq \frac{1}{{\pi }^2}$. Therefore for moderately large $x$, when $\frac{1}{{\pi }^2{x}^3}$ is negligible compared with $\frac{1}{2}$, the second term in the approximation for $x>3$ may be dropped. For very large $x$, when $\frac{1}{\pi x}$ becomes negligible, $C\left(x\right)\simeq \frac{1}{2}$. However there will be considerable difficulties in calculating $\sin \left(\frac{\pi }{2}{x}^2\right)$ accurately before this final limiting value can be used. Since $\sin \left(\frac{\pi }{2}{x}^2\right)$ is periodic, its value is essentially determined by the fractional part of $x^2$. If $x^2=N+\theta$, where $N$ is an integer and $0\le \theta <1$, then $\sin \left(\frac{\pi }{2}{x}^2\right)$ depends on $\theta$ and on $N$ modulo $4$. By exploiting this fact, it is possible to retain some significance in the calculation of $\sin \left(\frac{\pi }{2}{x}^2\right)$ either all the way to the very large $x$ limit, or at least until the integer part of $\frac{x}{2}$ is equal to the maximum integer allowed on the machine.

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

There are no failure exits from s20ad. The parameter _ifail has been included for consistency with other methods in this chapter.

Let $\delta$ and $\epsilon$ be the relative errors in the argument and result respectively.

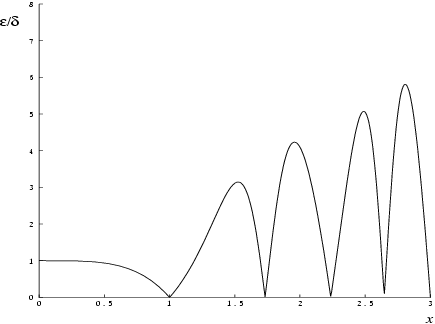
If $\delta$ is somewhat larger than the machine precision (i.e if $\delta$ is due to data errors etc.), then $\epsilon$ and $\delta$ are approximately related by: Figure 1 shows the behaviour of the error amplification factor $\left|\frac{x\cos \left(\frac{\pi }{2}{x}^2\right)}{C\left(x\right)}\right|$.

However, if $\delta$ is of the same order as the machine precision, then rounding errors could make $\epsilon$ slightly larger than the above relation predicts.

For small $x$, $\epsilon \simeq \delta$ and there is no amplification of relative error.

For moderately large values of $x$, and the result will be subject to increasingly large amplification of errors. However the above relation breaks down for large values of $x$ (i.e., when $\frac{1}{x^2}$ is of the order of the machine precision); in this region the relative error in the result is essentially bounded by $\frac{2}{\pi x}$.

Hence the effects of error amplification are limited and at worst the relative error loss should not exceed half the possible number of significant figures.

None.

None.

This example reads values of the argument $x$ from a file, evaluates the function at each value of $x$ and prints the results.