s14aa returns the value of the gamma function

Γ (x)

Syntax

C#
public static double s14aa( double x, out int ifail )

Visual Basic
Public Shared Function s14aa ( _ x As Double, _ <OutAttribute> ByRef ifail As Integer _ ) As Double

Visual C++
public: static double s14aa( double x, [OutAttribute] int% ifail )

F#
static member s14aa : x : float * ifail : int byref -> float

Parameters

x: Type: System..::..Double
On entry: the argument $x$ of the function.

Constraint: $x$ must not be zero or a negative integer.

ifail: Type: System..::..Int32%
On exit: $ifail = 0$ unless the method detects an error or a warning has been flagged (see [Error Indicators and Warnings]).

Return Value

s14aa returns the value of the gamma function

Γ (x)

Description

s14aa evaluates an approximation to the gamma function

Γ (x)

. The method is based on the Chebyshev expansion:

Γ (1 + u) = \sum_{r = 0}^{'} a_{r} T_{r} (t),   where ​ 0 \leq u < 1, t = 2 u - 1,

and uses the property

Γ (1 + x) = x Γ (x)

. If

x = N + 1 + u

where

N

is integral and

0 \leq u < 1

then it follows that:

for $N > 0$ , $Γ (x) = (x - 1) (x - 2) \dots (x - N) Γ (1 + u)$ ,
for $N = 0$ , $Γ (x) = Γ (1 + u)$ ,
for $N < 0$ , $Γ (x) = \frac{Γ (1 + u)}{x (x + 1) (x + 2) \dots (x - N - 1)}$ .

There are four possible failures for this method:

(i)	if $x$ is too large, there is a danger of overflow since $Γ (x)$ could become too large to be represented in the machine;
(ii)	if $x$ is too large and negative, there is a danger of underflow;
(iii)	if $x$ is equal to a negative integer, $Γ (x)$ would overflow since it has poles at such points;
(iv)	if $x$ is too near zero, there is again the danger of overflow on some machines. For small $x$ , $Γ (x) ≃ 1 / x$ , and on some machines there exists a range of nonzero but small values of $x$ for which $1 / x$ is larger than the greatest representable value.

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Error Indicators and Warnings

Errors or warnings detected by the method:

$ifail = 1$: The argument is too large. On failure the method returns the approximate value of $Γ (x)$ at the nearest valid argument.

$ifail = 2$: The argument is too large and negative. On failure the method returns zero.

$ifail = 3$: The argument is too close to zero. On failure the method returns the approximate value of $Γ (x)$ at the nearest valid argument.

$ifail = 4$: The argument is a negative integer, at which value $Γ (x)$ is infinite. On failure the method returns a large positive value.

$ifail = -9000$: An error occured, see message report.

Accuracy

Let

δ

and

ε

be the relative errors in the argument and the result respectively. If

δ

is somewhat larger than the machine precision (i.e., is due to data errors etc.), then

ε

and

δ

are approximately related by:

ε ≃ |x Ψ (x)| δ

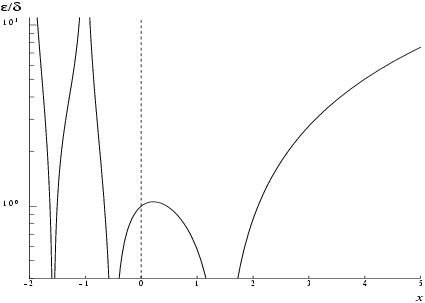
(provided

ε

is also greater than the representation error). Here

Ψ (x)

is the digamma function

\frac{Γ^{'} (x)}{Γ (x)}

. Figure 1 shows the behaviour of the error amplification factor

|x Ψ (x)|

δ

is of the same order as machine precision, then rounding errors could make

ε

slightly larger than the above relation predicts.

There is clearly a severe, but unavoidable, loss of accuracy for arguments close to the poles of

Γ (x)

at negative integers. However relative accuracy is preserved near the pole at

x = 0

right up to the point of failure arising from the danger of overflow.

Also accuracy will necessarily be lost as

x

becomes large since in this region

ε ≃ δ x \ln x .

However since

Γ (x)

increases rapidly with

x

, the method must fail due to the danger of overflow before this loss of accuracy is too great. (For example, for

x = 20

, the amplification factor

≃ 60

Figure 1

Parallelism and Performance

None.

Further Comments

None.

Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Example program (C#): s14aae.cs

Example program data: s14aae.d

Example program results: s14aae.r