public static double s10ab(
	double x,
	out int ifail
)

Public Shared Function s10ab ( _
	x As Double, _
	<OutAttribute> ByRef ifail As Integer _
) As Double

public:
static double s10ab(
	double x, 
	[OutAttribute] int% ifail
)

static member s10ab : 
        x : float * 
        ifail : int byref -> float 

s10ab returns the value of the hyperbolic sine, $\sinh x$.

s10ab calculates an approximate value for the hyperbolic sine of its argument, $\sinh x$.

For $\left|x\right|\le 1$ it uses the Chebyshev expansion where $t=2x^2-1$.

For $1<\left|x\right|\le E_1\text{, \hspace{1em}}\sinh x=\frac{1}{2}\left(e^x-e^{-x}\right)$

where $E_1$ is a machine-dependent constant, details of which are given in the Users' Note for your implementation.

For $\left|x\right|>E_1$, the method fails owing to the danger of setting overflow in calculating $e^x$. The result returned for such calls is $\sinh \left(\mathrm{sign} x{E}_1\right)$, i.e., it returns the result for the nearest valid argument.

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Errors or warnings detected by the method:

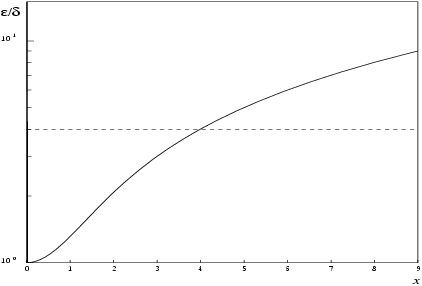
If $\delta$ and $\epsilon$ are the relative errors in the argument and result, respectively, then in principle

That is the relative error in the argument, $x$, is amplified by a factor, approximately $x\coth x$. The equality should hold if $\delta$ is greater than the machine precision ($\delta$ is a result of data errors etc.) but, if $\delta$ is simply a result of round-off in the machine representation of $x$, then it is possible that an extra figure may be lost in internal calculation round-off.

The behaviour of the error amplification factor can be seen in the following graph:

It should be noted that for $\left|x\right|\ge 2$  where $\Delta$ is the absolute error in the argument.

None.

None.

This example reads values of the argument $x$ from a file, evaluates the function at each value of $x$ and prints the results.