NAG Library Function Document
nag_exp_integral (s13aac)
1 Purpose
nag_exp_integral (s13aac) returns the value of the exponential integral .
2 Specification
| #include <nag.h> |
| #include <nags.h> |
| double |
nag_exp_integral (double x,
NagError *fail) |
|
3 Description
nag_exp_integral (s13aac) calculates an approximate value for
using Chebyshev expansions, where
is real. For
, the real part of the principal value of the integral is taken. The value
is infinite, and so, when
, nag_exp_integral (s13aac) exits with an error and returns the largest representable machine number.
For
,
where
.
For
,
where
.
In both cases, .
For
, the approximation is based on expansions proposed by
Cody and Thatcher Jr. (1969). Precautions are taken to maintain good relative accuracy in the vicinity of
, which corresponds to a simple zero of Ei(
).
nag_exp_integral (s13aac) guards against producing underflows and overflows by using the argument
; see the
Users' Note for your implementation for the value of
. To guard against overflow, if
the function terminates and returns the negative of the largest representable machine number. To guard against underflow, if
the result is set directly to zero.
4 References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Cody W J and Thatcher Jr. H C (1969) Rational Chebyshev approximations for the exponential integral Ei Math. Comp. 23 289–303
5 Arguments
- 1:
x – doubleInput
On entry: the argument of the function.
Constraint:
or .
- 2:
fail – NagError *Input/Output
-
The NAG error argument (see
Section 3.6 in the Essential Introduction).
6 Error Indicators and Warnings
- NE_INTERNAL_ERROR
-
An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact
NAG for assistance.
- NE_REAL_ARG_LE
-
On entry, and the function is infinite.
The evaluation has been abandoned due to the likelihood of overflow. The argument .
7 Accuracy
Unless stated otherwise, it is assumed that .
If
and
are the relative errors in argument and result respectively, then in principle,
so the relative error in the argument is amplified in the result by at least a factor
. The equality should hold if
is greater than the
machine precision (
due to data errors etc.) but if
is simply a result of round-off in the machine representation, it is possible that an extra figure may be lost in internal calculation and round-off.
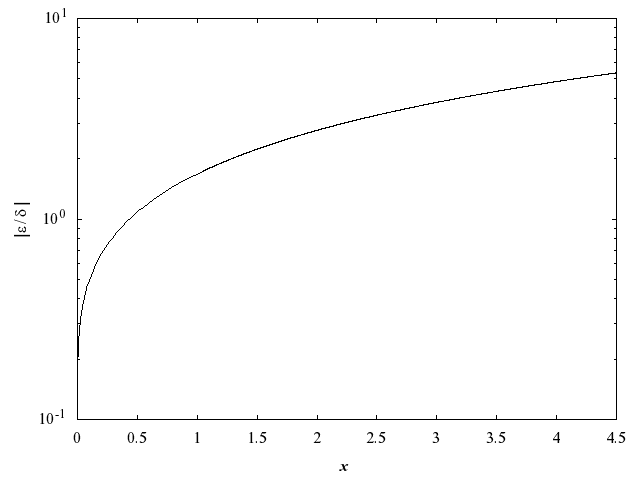
The behaviour of this amplification factor is shown in the following graph:
Figure 1
It should be noted that, for absolutely small , the amplification factor tends to zero and eventually the error in the result will be limited by machine precision.
For absolutely large
,
the absolute error in the argument.
For , empirical tests have shown that the maximum relative error is a loss of approximately decimal place.
8 Parallelism and Performance
Not applicable.
None.
10 Example
The following program reads values of the argument from a file, evaluates the function at each value of and prints the results.
10.1 Program Text
Program Text (s13aace.c)
10.2 Program Data
Program Data (s13aace.d)
10.3 Program Results
Program Results (s13aace.r)