Calling NAG Library Routines from Scilab
NAG Technical Report TR 5/09

Nathaniel Fenton
Numerical Algorithms Group, August 2009

Start of report   Skip to Example 1   Skip to Example 2   Skip to Example 3   Skip to Example 4   Skip to Example 5 Reference Page

Abstract

This report gives detailed instructions on how to call routines in the NAG C and Fortran Libraries from the Scilab programming environment.

Contents

  1. Introduction
  2. C code and Scilab sce Files
  3. Examples
  4. Summary
  5. Reference Page
  6. References

1. Introduction

Scilab [1] is a freely distributed scientific software package that contains hundreds of mathematical functions and can be extended by adding in other functions. The NAG Libraries [2] contain a large selection of numerical and statistical routines, which can be accessed from different languages [3]. We will briefly describe one of the ways in which the NAG library can be interfaced with Scilab, and give some examples of how this is done.

In order to call the NAG functions within Scilab, one can either statically or dynamically link the required NAG function by writing a simple interface which acts as the glue between the NAG library and Scilab. The linked function can then be used like any other Scilab function. Both the NAG C library and the NAG Fortran library can be linked, but as Scilab is written in C we will first look at linking the C library via an interface also written in C. We will only discuss how to dynamically link the NAG routines.

2. C code and Scilab sce Files

Scilab has a function ilib_build which we shall be using to compile our C code into a dynamically linked library. This in turn can then be linked into Scilab using the addinter function. All that needs to be done is to write a C interface calling the NAG function that we require and then use the two functions mentioned above to compile and link. Our interface written in C will look something like this

    #include <stack-c.h>
    #include appropriate NAG header files

    int interface name (char *fname)
    {

    retrieve input arguments from the Scilab stack
    call NAG routine
    assign output arguments

    return 0;
    }

where:

  • stack-c.h contains the necessary functions for interacting with the Scilab stack, where all the input and output variables are kept
  • interface name is our name given to the interface which will be used later
  • fname will be our function name seen in Scilab. It doesn't need to be passed in by the user, but is passed in automatically by Scilab.

The Scilab builder script that we will execute in Scilab in order to compile our interface is based on this template:

    // This is the builder.sce
    // must be run from this directory

    ilib_name  = 'nag_tute';  // interface library name
    files = ['nag_intext1.c'];     // files to compile

    libs  = [/opt/NAG/cll6a08dgl/lib/libnagc_nag]; // other libs needed for linking
    table = [ 'function_name' 'interface name'];
    cflags = '-I/opt/NAG/cll6a08dgl/include'       // flags needed for the C compiler

    // do not modify below
    // ----------------------------------------------
    ilib_build(ilib_name,table,files,libs,[],[],cflags);

It is assumed that your copy of the NAG C Library is installed in the default location /opt/NAG/cll6a08dgl. If this is not the case then you must edit the script appropriately. Note that:

  • this is the only file for building and linking that needs to be modified to compile the interface and link it with the NAG library. On running this builder script in Scilab, a loader script is automatically generated which doesn't need to be modified and runs the addinter function that was mentioned above.
  • ilib_name is the name given to the library to be linked
  • files is a list of files necessary for compilation, i.e. the interface files
  • libs contains any libraries needed for linking. Notice that we do not include the file extension .a or .so for libnagc_nag
  • function_name is the function name to be used in Scilab e.g. [output variables] = function_name(input variables). This can be chosen to be the same name as used within the NAG library if desired, whether the short name e.g. a00aac/a00aaf or the long name nag_implementation_details. Do not give the interface interface name one of these names as this will cause problems.

3. Examples

The rest of the code required will be easier to demonstrate with the use of examples. The code for this article was tested on a Linux machine running 64-bit Red Hat Linux 4.1.2-33 with Scilab 5.1.1. For the C examples, gcc (GCC) 4.4.0 and the gcc version of Mark 8 of the NAG C Library (cll6a08dg) were used. For the Fortran example, GNU Fortran (GCC) 4.4.0 and the GNU Fortran Mark 22 version of the NAG Fortran Library (fll6a22dg) were used.
IMPORTANT: in order for shared libraries to be located at run-time, it may be necessary for the environment variable LD_LIBRARY_PATH to be set correctly. See the Reference Page for more details.

3.1 Example 1  Dawson's Integral F(x)

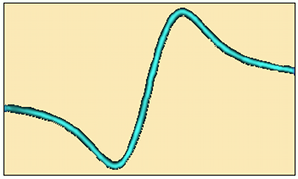dawson The simplest example: we call a function with only one return value – the routine nag_dawson (s15afc) from the NAG C Library which returns a value for Dawson's integral.
Files: Builder1, Interface1, Example1.

3.2 Example 2 General Elliptic Integral of the Second Kind

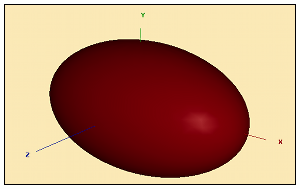elliptic We call a function with complex input and output values – nag_elliptic_integral_f (s21dac), which evaluates an approximation to the general elliptic integral of the second kind for complex z. Complex numbers are stored differently in Scilab and NAG C Library, so extra code is required to copy input data from the Scilab complex type into the NAG complex type and vice versa.
Files: Builder2, Interface2, Example2.

3.3 Example 3  Complex Eigenvalues and Eigenvectors of a Complex General Matrix

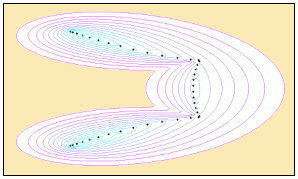eigvals We call a function which has some complex array input and outputs – nag_complex_eigensystem_sel (f02gcc). This function computes selected eigenvalues and the corresponding right eigenvectors of a general complex matrix A. Again, some copying between Scilab and NAG complex types is required.
Files: Builder3, Interface3, Example3.

3.4 Example 4  Evaluating a multi-dimensional integral

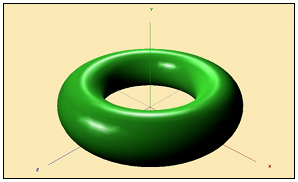torus In this example we call the multi-dimensional quadrature routine nag_multid_quad_adapt_1 (d01wcc). The routine takes as input a user-supplied function. We show two ways of supplying the function - either as C code or Scilab code.

Files: Builder4a, Interface4a, Example4a. (for user defined function written in C)
Files: Builder4b, Interface4b, Example4b. (for user defined function written in Scilab)

3.5 Example 5  Pseudorandom Numbers taken from the Normal Distribution

pseudorand We call a function from NAG Fortran Library - G05LAF. This function returns a vector of pseudorandom numbers generated from a Normal distribution with mean µ and variance s2 We use NAG header files [4] for the NAG Fortran Library.
Files: Builder5, Interface5, Example5.

4. Summary

  • You can connect Scilab to the NAG C library or NAG Fortran library
  • You must write an interface that is the glue between the NAG library and Scilab
  • Scilab has built-in functions that make it relatively easy to link to the NAG library
  • At run time you need to make sure that any necessary environment variable is pointing at the correct NAG library

5. Reference Page

A lot of useful information is condensed from the five examples into one page for reference purposes. It also contains some links to websites with more information on writing interfaces for functions to Scilab, and some hints on some common troubleshooting issues.

References

Start of report   Skip to Example 1   Skip to Example 2   Skip to Example 3   Skip to Example 4   Skip to Example 5 Reference Page

Copyright 2009 Numerical Algorithms Group
[NP3675]