NAG Library Routine Document
g03ehf
(cluster_hier_dendrogram)
1
Purpose
g03ehf produces a dendrogram from the results of
g03ecf.
2
Specification
Fortran Interface
| Integer, Intent (In) | :: |
n,
nsym,
lenc | | Integer, Intent (Inout) | :: |
ifail | | Real (Kind=nag_wp), Intent (In) | :: |
dord(n),
dmin,
dstep | | Character (*), Intent (Out) | :: |
c(lenc) | | Character (1), Intent (In) | :: |
orient |
|
C Header Interface
|
#include nagmk26.h
| void |
g03ehf_ (
const char *orient,
const Integer *n,
const double dord[],
const double *dmin,
const double *dstep,
const Integer *nsym,
char c[],
const Integer *lenc,
Integer *ifail,
const Charlen length_orient,
const Charlen length_c) |
|
3
Description
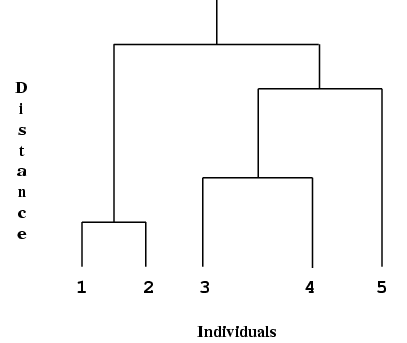
Hierarchical cluster analysis, as performed by
g03ecf, can be represented by a tree that shows at which distance the clusters merge. Such a tree is known as a dendrogram. See
Everitt (1974) and
Krzanowski (1990) for examples of dendrograms. A simple example is,
The end points of the dendrogram represent the objects that have been clustered. They should be in a suitable order as given by
g03ecf. Object
is always the first object. In the example above the height represents the distance at which the clusters merge.
The dendrogram is produced in
a character array
using the ordering and distances provided by
g03ecf. Suitable characters are used to represent parts of the tree.
There are four possible orientations for the dendrogram. The example above has the end points at the bottom of the diagram which will be referred to as south. If the dendrogram was the other way around with the end points at the top of the diagram then the orientation would be north. If the end points are at the left-hand or right-hand side of the diagram the orientation is west or east. Different symbols are used for east/west and north/south orientations.
4
References
Everitt B S (1974) Cluster Analysis Heinemann
Krzanowski W J (1990) Principles of Multivariate Analysis Oxford University Press
5
Arguments
- 1: – Character(1)Input
-
On entry: indicates which orientation the dendrogram is to take.
- The end points of the dendrogram are to the north.
- The end points of the dendrogram are to the south.
- The end points of the dendrogram are to the east.
- The end points of the dendrogram are to the west.
Constraint:
, , or .
- 2: – IntegerInput
-
On entry: the number of objects in the cluster analysis.
Constraint:
.
- 3: – Real (Kind=nag_wp) arrayInput
-
On entry: the array
dord as output by
g03ecf.
dord contains the distances, in dendrogram order, at which clustering takes place.
Constraint:
, for .
- 4: – Real (Kind=nag_wp)Input
-
On entry: the clustering distance at which the dendrogram begins.
Constraint:
.
- 5: – Real (Kind=nag_wp)Input
-
On entry: the distance represented by one symbol of the dendrogram.
Constraint:
.
- 6: – IntegerInput
-
On entry: the number of character positions used in the dendrogram. Hence the clustering distance at which the dendrogram terminates is given by .
Constraint:
.
- 7: – Character(*) arrayOutput
-
Note: the length of each element of
c must be at least
if
or
, or at least
nsym if
or
.
On exit: the elements of
c contain consecutive lines of the dendrogram.
- 8: – IntegerInput
-
On entry: the dimension of the array
c as declared in the (sub)program from which
g03ehf is called.
Constraints:
- if or , ;
- if or , .
- 9: – IntegerInput/Output
-
On entry:
ifail must be set to
,
. If you are unfamiliar with this argument you should refer to
Section 3.4 in How to Use the NAG Library and its Documentation for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this argument, the recommended value is
.
When the value is used it is essential to test the value of ifail on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
6
Error Indicators and Warnings
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
x04aaf).
Errors or warnings detected by the routine:
-
| On entry, | , |
| or | , |
| or | , |
| or | , |
| or | , or 'W', |
| or | or , , |
| or | or , , |
| or | the number of characters that can be stored in each element of array c is insufficient for the requested orientation. |
-
| On entry, | , for some . |
An unexpected error has been triggered by this routine. Please
contact
NAG.
See
Section 3.9 in How to Use the NAG Library and its Documentation for further information.
Your licence key may have expired or may not have been installed correctly.
See
Section 3.8 in How to Use the NAG Library and its Documentation for further information.
Dynamic memory allocation failed.
See
Section 3.7 in How to Use the NAG Library and its Documentation for further information.
7
Accuracy
Not applicable.
8
Parallelism and Performance
g03ehf is not threaded in any implementation.
The scale of the dendrogram is controlled by
dstep. The smaller the value
dstep is, the greater the amount of detail that will be given but
nsym will have to be larger to give the full dendrogram. The range of distances represented by the dendrogram is
dmin to
. The values of
dmin,
dstep and
nsym can thus be set so that only part of the dendrogram is produced.
The dendrogram does not include any labelling of the objects. You can print suitable labels using the ordering given by the array
iord returned by
g03ecf.
10
Example
Data consisting of three variables on five objects are read in. Euclidean squared distances are computed using
g03eaf and median clustering performed by
g03ecf.
g03ehf is used to produce a dendrogram with orientation east and a dendrogram with orientation south. The two dendrograms are printed.
10.1
Program Text
Program Text (g03ehfe.f90)
10.2
Program Data
Program Data (g03ehfe.d)
10.3
Program Results
Program Results (g03ehfe.r)