NAG Library Routine Document
f04qaf (real_gen_sparse_lsqsol)
1
Purpose
f04qaf solves sparse nonsymmetric equations, sparse linear least squares problems and sparse damped linear least squares problems, using a Lanczos algorithm.
2
Specification
Fortran Interface
| Subroutine f04qaf ( |
m, n, b, x, se, aprod, damp, atol, btol, conlim, itnlim, msglvl, itn, anorm, acond, rnorm, arnorm, xnorm, work, ruser, lruser, iuser, liuser, inform, ifail) |
| Integer, Intent (In) | :: | m, n, msglvl, lruser, liuser | | Integer, Intent (Inout) | :: | itnlim, iuser(liuser), ifail | | Integer, Intent (Out) | :: | itn, inform | | Real (Kind=nag_wp), Intent (In) | :: | damp, atol, btol, conlim | | Real (Kind=nag_wp), Intent (Inout) | :: | b(m), ruser(lruser) | | Real (Kind=nag_wp), Intent (Out) | :: | x(n), se(n), anorm, acond, rnorm, arnorm, xnorm, work(n,2) | | External | :: | aprod |
|
C Header Interface
|
#include <nagmk26.h>
| void |
f04qaf_ (const Integer *m, const Integer *n, double b[], double x[], double se[],
void (NAG_CALL *aprod)(Integer *mode, const Integer *m, const Integer *n, double x[], double y[], double ruser[], const Integer *lruser, Integer iuser[], const Integer *liuser),
const double *damp, const double *atol, const double *btol, const double *conlim, Integer *itnlim, const Integer *msglvl, Integer *itn, double *anorm, double *acond, double *rnorm, double *arnorm, double *xnorm, double work[], double ruser[], const Integer *lruser, Integer iuser[], const Integer *liuser, Integer *inform, Integer *ifail) |
|
3
Description
f04qaf can be used to solve a system of linear equations
where
is an
by
sparse nonsymmetric matrix, or can be used to solve linear least squares problems, so that
f04qaf minimizes the value
given by
where
is an
by
sparse matrix and
denotes the Euclidean length of
so that
. A damping argument,
, may be included in the least squares problem in which case
f04qaf minimizes the value
given by
is supplied as the argument
damp and should of course be zero if the solution to problems
(1) or
(2) is required. Minimizing
in
(3) is often called ridge regression.
f04qaf is based upon algorithm LSQR (see
Paige and Saunders (1982a) and
Paige and Saunders (1982b)) and solves the problems by an algorithm based upon the Lanczos process. The routine does not require
explicitly, but
is specified via
aprod which must perform the operations
and
for a given
-element vector
and
element vector
. A argument to
aprod specifies which of the two operations is required on a given entry.
The routine also returns estimates of the standard errors of the sample regression coefficients (
, for
) given by the diagonal elements of the estimated variance-covariance matrix
. When problem
(2) is being solved and
is of full rank, then
is given by
and when problem
(3) is being solved then
is given by
Let
denote the matrix
let
denote the residual vector
corresponding to an iterate
, so that
is the function being minimized, and let
denote the Frobenius (Euclidean) norm of
. Then the routine accepts
as a solution if it is estimated that one of the following two conditions is satisfied:
where
and
are user-supplied tolerances which estimate the relative errors in
and
respectively. Condition
(6) is appropriate for compatible problems where, in theory, we expect the residual to be zero and will be satisfied by an acceptable solution
to a compatible problem. Condition
(7) is appropriate for incompatible systems where we do not expect the residual to be zero and is based on the observation that, in theory,
when
is a solution to the least squares problem, and so
(7) will be satisfied by an acceptable solution
to a linear least squares problem.
The routine also includes a test to prevent convergence to solutions,
, with unacceptably large elements. This can happen if
is nearly singular or is nearly rank deficient. If we let the singular values of
be
then the condition number of
is defined as
where
is the smallest nonzero singular value of
and hence
is the rank of
. When
, then
is rank deficient, the least squares solution is not unique and
f04qaf will normally converge to the minimal length solution. In practice
will not have exactly zero singular values, but may instead have small singular values that we wish to regard as zero.
The routine provides for this possibility by terminating if
where
is a user-supplied limit on the condition number of
. For problem
(1) termination with this condition indicates that
is nearly singular and for problem
(2) indicates that
is nearly rank deficient and so has near linear dependencies in its columns. In this case inspection of
,
and
, which are all returned by the routine, will indicate whether or not an acceptable solution has been found. Condition
(8), perhaps in conjunction with
, can be used to try and ‘regularize’ least squares solutions. A full discussion of the stopping criteria is given in Section 6 of
Paige and Saunders (1982a).
Introduction of a nonzero damping argument
tends to reduce the size of the computed solution and to make its components less sensitive to changes in the data, and
f04qaf is applicable when a value of
is known
a priori. To have an effect,
should normally be at least
where
is the
machine precision. For further discussion see
Paige and Saunders (1982b) and the references given there.
Whenever possible the matrix should be scaled so that the relative errors in the elements of are all of comparable size. Such a scaling helps to prevent the least squares problem from being unnecessarily sensitive to data errors and will normally reduce the number of iterations required. At the very least, in the absence of better information, the columns of should be scaled to have roughly equal column length.
4
References
Paige C C and Saunders M A (1982a) LSQR: An algorithm for sparse linear equations and sparse least squares ACM Trans. Math. Software 8 43–71
Paige C C and Saunders M A (1982b) Algorithm 583 LSQR: Sparse linear equations and least squares problems ACM Trans. Math. Software 8 195–209
5
Arguments
- 1: – IntegerInput
-
On entry: , the number of rows of the matrix .
Constraint:
.
- 2: – IntegerInput
-
On entry: , the number of columns of the matrix .
Constraint:
.
- 3: – Real (Kind=nag_wp) arrayInput/Output
-
On entry: the right-hand side vector .
On exit:
b is overwritten.
- 4: – Real (Kind=nag_wp) arrayOutput
-
On exit: the solution vector .
- 5: – Real (Kind=nag_wp) arrayOutput
-
On exit: the estimates of the standard errors of the components of
. Thus
contains an estimate of
, where
is the
th diagonal element of the estimated variance-covariance matrix
. The estimates returned in
se will be the lower bounds on the actual estimated standard errors, but will usually be correct to at least one significant figure.
- 6: – Subroutine, supplied by the user.External Procedure
-
aprod must perform the operations
and
for given vectors
and
.
The specification of
aprod is:
Fortran Interface
| Integer, Intent (In) | :: | m, n, lruser, liuser | | Integer, Intent (Inout) | :: | mode, iuser(liuser) | | Real (Kind=nag_wp), Intent (Inout) | :: | x(n), y(m), ruser(lruser) |
|
C Header Interface
|
#include <nagmk26.h>
| void |
aprod (Integer *mode, const Integer *m, const Integer *n, double x[], double y[], double ruser[], const Integer *lruser, Integer iuser[], const Integer *liuser) |
|
- 1: – IntegerInput/Output
-
On entry: specifies which operation is to be performed.
- aprod must compute .
- aprod must compute .
On exit: may be used as a flag to indicate a failure in the computation of
or
. If
mode is negative on exit from
aprod,
f04qaf will exit immediately with
ifail set to
mode.
- 2: – IntegerInput
-
On entry: , the number of rows of .
- 3: – IntegerInput
-
On entry: , the number of columns of .
- 4: – Real (Kind=nag_wp) arrayInput/Output
-
On entry: the vector .
On exit: if
,
x must be unchanged.
If
,
x must contain
.
- 5: – Real (Kind=nag_wp) arrayInput/Output
-
On entry: the vector .
On exit: if
,
y must contain
.
If
,
y must be unchanged.
- 6: – Real (Kind=nag_wp) arrayUser Workspace
- 7: – IntegerInput
- 8: – Integer arrayUser Workspace
- 9: – IntegerInput
-
aprod is called with the arguments
ruser,
lruser,
iuser and
liuser as supplied to
f04qaf. You should use the arrays
ruser,
lruser,
iuser and
liuser to supply information to
aprod.
aprod must either be a module subprogram USEd by, or declared as EXTERNAL in, the (sub)program from which
f04qaf is called. Arguments denoted as
Input must
not be changed by this procedure.
Note: aprod should not return floating-point NaN (Not a Number) or infinity values, since these are not handled by
f04qaf. If your code inadvertently
does return any NaNs or infinities,
f04qaf is likely to produce unexpected results.
- 7: – Real (Kind=nag_wp)Input
-
On entry: the value
. If either problem
(1) or problem
(2) is to be solved,
damp must be supplied as zero.
- 8: – Real (Kind=nag_wp)Input
-
On entry: the tolerance,
, of the convergence criteria
(6) and
(7); it should be an estimate of the largest relative error in the elements of
. For example, if the elements of
are correct to about
significant figures, then
atol should be set to about
. If
atol is supplied as less than
, where
is the
machine precision, the value
is used instead of
atol.
- 9: – Real (Kind=nag_wp)Input
-
On entry: the tolerance,
, of the convergence criterion
(6); it should be an estimate of the largest relative error in the elements of
. For example, if the elements of
are correct to about
significant figures, then
btol should be set to about
. If
btol is supplied as less than
, the value
is used instead of
btol.
- 10: – Real (Kind=nag_wp)Input
-
On entry: the value
of equation
(8); it should be an upper limit on the condition number of
.
conlim should not normally be chosen much larger than
. If
conlim is supplied as zero, the value
is used instead of
conlim.
- 11: – IntegerInput/Output
-
On entry: an upper limit on the number of iterations. If
, the value
n is used in place of
itnlim, but for ill-conditioned problems a higher value of
itnlim is likely to be necessary.
On exit: unchanged unless
on entry, in which case it is set to
n.
- 12: – IntegerInput
-
On entry: the level of printing from
f04qaf. If
, then no printing occurs, but otherwise messages will be output on the advisory message channel (see
x04abf). A description of the printed output is given in
Section 9.1. The level of printing is determined as follows:
- No printing.
- A brief summary is printed just prior to return from f04qaf.
- A summary line is printed periodically to monitor the progress of f04qaf, together with a brief summary just prior to return from f04qaf.
- 13: – IntegerOutput
-
On exit: the number of iterations performed.
- 14: – Real (Kind=nag_wp)Output
-
On exit: an estimate of
for the matrix
of
(4).
- 15: – Real (Kind=nag_wp)Output
-
On exit: an estimate of which is a lower bound.
- 16: – Real (Kind=nag_wp)Output
-
On exit: an estimate of
for the residual,
, of
(5) corresponding to the solution
returned in
x. Note that
is the function being minimized.
- 17: – Real (Kind=nag_wp)Output
-
On exit: an estimate of the
corresponding to the solution
returned in
x.
- 18: – Real (Kind=nag_wp)Output
-
On exit: an estimate of
for the solution
returned in
x.
- 19: – Real (Kind=nag_wp) arrayWorkspace
-
- 20: – Real (Kind=nag_wp) arrayUser Workspace
-
ruser is not used by
f04qaf, but is passed directly to
aprod and may be used to pass information to this routine.
- 21: – IntegerInput
-
On entry: the dimension of the array
ruser as declared in the (sub)program from which
f04qaf is called.
Constraint:
.
- 22: – Integer arrayUser Workspace
-
iuser is not used by
f04qaf, but is passed directly to
aprod and may be used to pass information to this routine.
- 23: – IntegerInput
-
On entry: the dimension of the array
iuser as declared in the (sub)program from which
f04qaf is called.
Constraint:
.
- 24: – IntegerOutput
-
On exit: the reason for termination of
f04qaf.
- The exact solution is . No iterations are performed in this case.
- The termination criterion of (6) has been satisfied with and as the values supplied in atol and btol respectively.
- The termination criterion of (7) has been satisfied with as the value supplied in atol.
- The termination criterion of (6) has been satisfied with and/or as the value , where is the machine precision. One or both of the values supplied in atol and btol must have been less than and was too small for this machine.
- The termination criterion of (7) has been satisfied with as the value . The value supplied in atol must have been less than and was too small for this machine.
The values
,
and
correspond to failure with
,
and
respectively (see
Section 6) and when
ifail is negative
inform will be set to the same negative value.
- 25: – IntegerInput/Output
-
On entry:
ifail must be set to
,
. If you are unfamiliar with this argument you should refer to
Section 3.4 in How to Use the NAG Library and its Documentation for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this argument, the recommended value is
.
When the value is used it is essential to test the value of ifail on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
6
Error Indicators and Warnings
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
x04aaf).
Errors or warnings detected by the routine:
-
On entry, .
Constraint: .
On entry, .
Constraint: .
On entry, .
Constraint: .
On entry, .
Constraint: .
-
Termination criteria not satisfied, but the condition number bound supplied in
conlim has been met.
The condition of
(8) has been satisfied for the value of
supplied in
conlim. If this failure is unexpected you should check that
aprod is working correctly. Although conditions
(6) or
(7) have not been satisfied, the values returned in
rnorm,
arnorm and
xnorm may nevertheless indicate that an acceptable solution has been reached.
-
Termination criteria not satisfied, but the condition number is bounded by
/
x02ajf.
The condition of
(8) has been satisfied for the value
, where
is the
machine precision. The matrix
is nearly singular or rank deficient and the problem is too ill-conditioned for this machine. If this failure is unexpected, you should check that
aprod is working correctly.
-
Maximum number of iterations reached.
The limit on the number of iterations has been reached. The number of iterations required by f04qaf and the condition of the matrix can depend strongly on the scaling of the problem. Poor scaling of the rows and columns of should be avoided whenever possible.
-
mode in
aprod has been set to:
.
An unexpected error has been triggered by this routine. Please
contact
NAG.
See
Section 3.9 in How to Use the NAG Library and its Documentation for further information.
Your licence key may have expired or may not have been installed correctly.
See
Section 3.8 in How to Use the NAG Library and its Documentation for further information.
Dynamic memory allocation failed.
See
Section 3.7 in How to Use the NAG Library and its Documentation for further information.
7
Accuracy
When the problem is compatible, the computed solution
will satisfy the equation
where an estimate of
is returned in the argument
rnorm. When the problem is incompatible, the computed solution
will satisfy the equation
where an estimate of
is returned in the argument
arnorm. See also Section 6.2 of
Paige and Saunders (1982b).
8
Parallelism and Performance
f04qaf makes calls to BLAS and/or LAPACK routines, which may be threaded within the vendor library used by this implementation. Consult the documentation for the vendor library for further information.
Please consult the
X06 Chapter Introduction for information on how to control and interrogate the OpenMP environment used within this routine. Please also consult the
Users' Note for your implementation for any additional implementation-specific information.
The time taken by
f04qaf is likely to be principally determined by the time taken in
aprod, which is called twice on each iteration, once with
and once with
. The time taken per iteration by the remaining operations in
f04qaf is approximately proportional to
.
The Lanczos process will usually converge more quickly if
is pre-conditioned by a nonsingular matrix
that approximates
in some sense and is also chosen so that equations of the form
can efficiently be solved for
. For a discussion of preconditioning, see the
F11 Chapter Introduction. In the context of
f04qaf, problem
(1) is equivalent to
and problem
(2) is equivalent to minimizing
Note that the normal matrix
so that the preconditioning
is equivalent to the preconditioning
of the normal matrix
.
Pre-conditioning can be incorporated into
f04qaf simply by coding
aprod to compute
and
in place of
and
respectively, and then solving the equations
for
on return from
f04qaf. The quantity
should be computed by solving
for
and then computing
, and
should be computed by solving
for
and then forming
.
9.1
Description of the Printed Output
When
, then
f04qaf will produce output (except in the case where the routine fails with
) on the advisory message channel (see
x04abf).
When
then a summary line is printed periodically giving the following information:
| Output |
Meaning |
| ITN |
Iteration number, . |
| X(1) |
The first element of the current iterate . |
| FUNCTION |
The current value of the function, , being minimized. |
| COMPAT |
An estimate of , where is the residual corresponding to . This value should converge to zero (in theory) if and only if the problem is compatible. COMPAT decreases monotonically. |
| INCOMPAT |
An estimate of which should converge to zero if and only if at the solution is nonzero. INCOMPAT is not usually monotonic. |
| NRM(ABAR) |
A monotonically increasing estimate of . |
| COND(ABAR) |
A monotonically increasing estimate of the condition number . |
10
Example
This example solves the linear least squares problem
where
is the
by
matrix and
is the
element vector given by
with
.
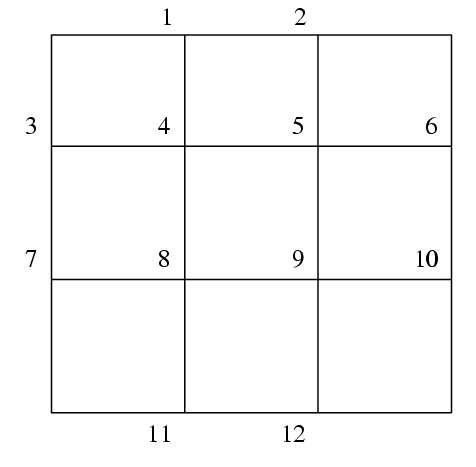
Such a problem can arise by considering the Neumann problem on a rectangle
where
is the boundary of the rectangle, and discretizing as illustrated below with the square mesh
Figure 1
The by symmetric part of represents the difference equations and the final row comes from the normalizing condition. The example program has at all the internal mesh points, but apart from this is written in a general manner so that the number of rows (NROWS) and columns (NCOLS) in the grid can readily be altered.
10.1
Program Text
Program Text (f04qafe.f90)
10.2
Program Data
Program Data (f04qafe.d)
10.3
Program Results
Program Results (f04qafe.r)