nag_cos_integral (s13acc) returns the value of the cosine integral
where
denotes Euler's constant.
For
it is based on the Chebyshev expansion
For
where the value of
is given in the
Users' Note for your implementation,
where
and
,
.
For
,
to within the accuracy possible (see
Section 7).
If
and
are the absolute and relative errors in the result and
is the relative error in the argument then in principle these are related by
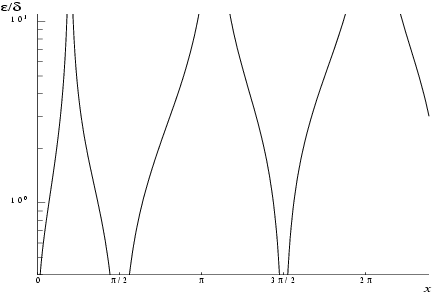
That is accuracy will be limited by
machine precision near the origin and near the zeros of
, but near the zeros of
only absolute accuracy can be maintained.
The behaviour of this amplification is shown in
Figure 1.
None.