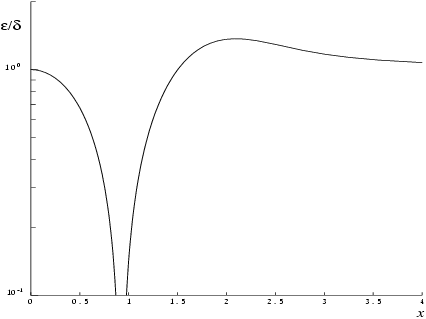
. If you are unfamiliar with this argument you should refer to
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this argument, the recommended value is
.
When the value is used it is essential to test the value of ifail on exit.