For
it is based on the Chebyshev expansion
For
it uses the fact that
This form is used directly for
, where
, and the machine uses approximately
decimal place arithmetic.
For
,
is equal to
to within the accuracy of the machine and hence we can guard against premature overflow and, without loss of accuracy, calculate
None.
If
and
are the relative errors in the argument and the result, respectively, then in principle
That is, the relative error in the argument,
, is amplified by a factor at least
, in the result.
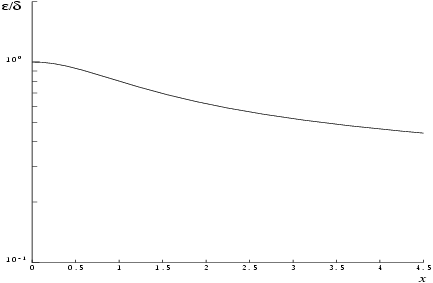
The behaviour of the amplification factor is shown in the following graph:
Figure 1
It should be noted that this factor is always less than or equal to one. For large
we have the absolute error in the result,
, in principle, given by
This means that eventually accuracy is limited by
machine precision.
None.