f01lhf factorizes a real almost block diagonal matrix,
, by row elimination with alternate row and column pivoting such that no ‘fill-in’ is produced. The code, which is derived from ARCECO described in
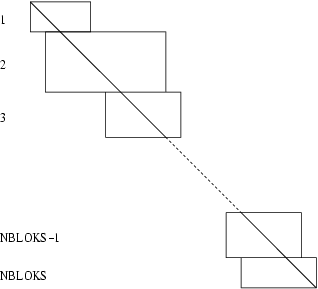
Diaz et al. (1983), uses Level 1 and Level 2 BLAS. No three successive diagonal blocks may have columns in common and therefore the almost block diagonal matrix must have the form shown in the following diagram:
Figure 1
This routine may be followed by
f04lhf, which is designed to solve sets of linear equations
or
.
Diaz J C, Fairweather G and Keast P (1983) Fortran packages for solving certain almost block diagonal linear systems by modified alternate row and column elimination ACM Trans. Math. Software 9 358–375
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
x04aaf).
Please consult the
X06 Chapter Introduction for information on how to control and interrogate the OpenMP environment used within this routine. Please also consult the
Users' Note for your implementation for any additional implementation-specific information.
Singularity or near singularity in
is determined by the argument
tol. If the absolute value of any pivot is less than
, where
is the maximum absolute value of an element of
, then
is said to be singular. The position on the diagonal of
of the first of any such pivots is indicated by the argument
kpivot. The factorization, and the test for near singularity, will be more accurate if before entry
is scaled so that the
-norms of the rows and columns of
are all of approximately the same order of magnitude. (The
-norm is the maximum absolute value of any element in the row or column.)
This example solves the set of linear equations
where
and
The exact solution is