A set of
data points with rectangular Cartesian coordinates
are sorted into panels defined by lines parallel to the
and
axes. The intercepts of these lines on the
and
axes are given in
, for
and
, for
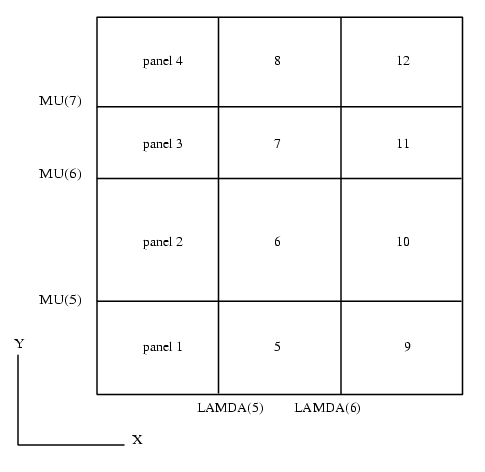
, respectively. The subroutine orders the data so that all points in a panel occur before data in succeeding panels, where the panels are numbered from bottom to top and then left to right, with the usual arrangement of axes, as shown in the diagram. Within a panel the points maintain their original order.
Figure 1
A data point lying exactly on one or more panel sides is taken to be in the highest-numbered panel adjacent to the point. The subroutine does not physically rearrange the data, but provides the array
point which contains a linked list for each panel, pointing to the data in that panel. The total number of panels is
.
None.
- 1: – IntegerInput
- 2: – IntegerInput
-
On entry:
px and
py must specify eight more than the number of intercepts on the
axis and
axis, respectively.
Constraint:
and .
- 3: – Real (Kind=nag_wp) arrayInput
-
On entry: to must contain, in nondecreasing order, the intercepts on the axis of the sides of the panels parallel to the axis.
- 4: – Real (Kind=nag_wp) arrayInput
-
On entry: to must contain, in nondecreasing order, the intercepts on the axis of the sides of the panels parallel to the axis.
- 5: – IntegerInput
-
On entry: the number of data points.
- 6: – Real (Kind=nag_wp) arrayInput
- 7: – Real (Kind=nag_wp) arrayInput
-
On entry: the coordinates of the
th data point , for .
- 8: – Integer arrayOutput
-
On exit: for
,
is the index of the first point in panel
,
is the index of the second point in panel
and so on.
indicates that was the last point in the panel.
The coordinates of points in panel
can be accessed in turn by means of the following instructions:
in = m + i
10 in = point(in)
If (in.eq. 0) Goto 20
xi = x(in)
yi = y(in)
.
.
.
Goto 10
20 ...
- 9: – IntegerInput
-
On entry: the dimension of the array
point as declared in the (sub)program from which
e02zaf is called.
Constraint:
.
- 10: – Integer arrayWorkspace
- 11: – IntegerInput
-
On entry: the value , the number of panels into which the plane is divided.
- 12: – IntegerInput/Output
-
On entry:
ifail must be set to
,
. If you are unfamiliar with this argument you should refer to
Section 3.4 in How to Use the NAG Library and its Documentation for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, if you are not familiar with this argument, the recommended value is
.
When the value is used it is essential to test the value of ifail on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
x04aaf).
Not applicable.
This subroutine was written to sort two-dimensional data in the manner required by routine
e02daf. The first
arguments of
e02zaf are the same as the arguments in
e02daf which have the same name.
This example reads in data points and the intercepts of the panel sides on the
and
axes; it calls
e02zaf to set up the index array
point; and finally it prints the data points in panel order.