NAG Library Routine Document

S09ABF

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Parameters

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

S09ABF returns the value of the inverse circular cosine,

\arccos x

, via the function name; the result is in the principal range

(0, π)

2 Specification

FUNCTION S09ABF (

X, IFAIL)

REAL (KIND=nag_wp) S09ABF

INTEGER	IFAIL
REAL (KIND=nag_wp)	X

3 Description

S09ABF calculates an approximate value for the inverse circular cosine,

\arccos x

. It is based on the Chebyshev expansion

\arcsin x = x \times y (t) = x \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t)

where

\frac{- 1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}},   and t = 4 x^{2} - 1

For

x^{2} \leq \frac{1}{2}, \arccos x = \frac{π}{2} - \arcsin x

For

- 1 \leq x < \frac{- 1}{\sqrt{2}}, \arccos x = π - \arcsin \sqrt{1 - x^{2}}

For

\frac{1}{\sqrt{2}} < x \leq 1, \arccos x = \arcsin \sqrt{1 - x^{2}}

For

|x| > 1, \arccos x

is undefined and the routine fails.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Parameters

1: $X$ – REAL (KIND=nag_wp)Input: On entry: the argument $x$ of the function.

Constraint: $|X| \leq 1.0$ .
2: $IFAIL$ – INTEGERInput/Output: On entry: IFAIL must be set to $0$ , $- 1 or 1$ . If you are unfamiliar with this parameter you should refer to Section 3.3 in the Essential Introduction for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value $- 1 or 1$ is recommended. If the output of error messages is undesirable, then the value $1$ is recommended. Otherwise, if you are not familiar with this parameter, the recommended value is $0$ . When the value $- 1 or 1$ is used it is essential to test the value of IFAIL on exit.

On exit: $IFAIL = 0$ unless the routine detects an error or a warning has been flagged (see Section 6).

6 Error Indicators and Warnings

If on entry

IFAIL = 0

- 1

, explanatory error messages are output on the current error message unit (as defined by X04AAF).

Errors or warnings detected by the routine:

$IFAIL = 1$: S09ABF has been called with $|X| > 1.0$ , for which arccos is undefined. A zero result is returned.

$IFAIL = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.
See Section 3.8 in the Essential Introduction for further information.

$IFAIL = - 399$: Your licence key may have expired or may not have been installed correctly.
See Section 3.7 in the Essential Introduction for further information.

$IFAIL = - 999$: Dynamic memory allocation failed.
See Section 3.6 in the Essential Introduction for further information.

7 Accuracy

δ

and

ε

are the relative errors in the argument and the result, respectively, then in principle

|ε| ≃ |\frac{x}{\arccos x \sqrt{1 - x^{2}}} \times δ| .

The equality should hold if

δ

is greater than the machine precision (

δ

is due to data errors etc.), but if

δ

is due simply to round-off in the machine it is possible that rounding etc. in internal calculations may lose one extra figure.

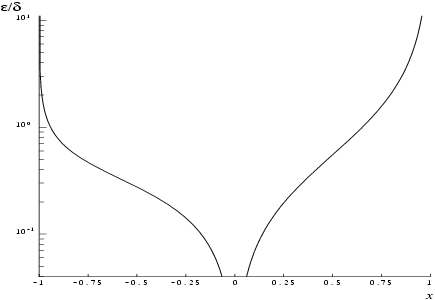
The behaviour of the amplification factor

\frac{x}{\arccos x \sqrt{1 - x^{2}}}

is shown in the graph below.

In the region of

x = 0

this factor tends to zero and the accuracy will be limited by the machine precision. For

|x|

close to one,

1 - |x| \sim δ

, the above analysis is not applicable owing to the fact that both the argument and the result are bounded

|x| \leq 1

0 \leq \arccos x \leq π

In the region of

x \sim - 1

we have

ε \sim \sqrt{δ}

, that is the result will have approximately half as many correct significant figures as the argument.

In the region

x \sim + 1

, we have that the absolute error in the result,

E

, is given by

E \sim \sqrt{δ}

, that is the result will have approximately half as many decimal places correct as there are correct figures in the argument.

Figure 1

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Routine DocumentS09ABF