NAG Library Function Document

nag_exp_integral (s13aac)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_exp_integral (s13aac) returns the value of the exponential integral

E_{1} (x)

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_exp_integral (double x, NagError *fail)

3 Description

nag_exp_integral (s13aac) calculates an approximate value for

E_{1} (x) = - Ei (- x) = \int_{x}^{\infty} \frac{e^{- u}}{u} d u .

using Chebyshev expansions, where

x

is real. For

x < 0

, the real part of the principal value of the integral is taken. The value

E_{1} (0)

is infinite, and so, when

x = 0

, nag_exp_integral (s13aac) exits with an error and returns the largest representable machine number.

For

0 < x \leq 4

E_{1} (x) = y (t) - \ln x = \underset{r}{\sum^{'}} a_{r} T_{r} (t) - \ln x,

where

t = \frac{1}{2} x - 1

For

x > 4

E_{1} (x) = \frac{e^{- x}}{x} y (t) = \frac{e^{- x}}{x} \underset{r}{\sum^{'}} a_{r} T_{r} (t),

where

t = - 1.0 + \frac{14.5}{(x + 3.25)} = \frac{11.25 - x}{3.25 + x}

In both cases,

- 1 \leq t \leq + 1

For

x < 0

, the approximation is based on expansions proposed by Cody and Thatcher Jr. (1969). Precautions are taken to maintain good relative accuracy in the vicinity of

x_{0} \approx - 0.372507 \dots

, which corresponds to a simple zero of Ei(

- x

nag_exp_integral (s13aac) guards against producing underflows and overflows by using the argument

x_{hi}

; see the Users' Note for your implementation for the value of

x_{hi}

. To guard against overflow, if

x < - x_{hi}

the function terminates and returns the negative of the largest representable machine number. To guard against underflow, if

x > x_{hi}

the result is set directly to zero.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Cody W J and Thatcher Jr. H C (1969) Rational Chebyshev approximations for the exponential integral Ei

(x)

Math. Comp. 23 289–303

5 Arguments

1: $x$ – doubleInput: On entry: the argument $x$ of the function.

Constraint: $- x_{hi} \leq x < 0.0$ or $x > 0.0$ .
2: $fail$ – NagError *Input/Output: The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 3.2.1.2 in the Essential Introduction for further information.
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.

An unexpected error has been triggered by this function. Please contact NAG.
See Section 3.6.6 in the Essential Introduction for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 3.6.5 in the Essential Introduction for further information.
NE_REAL_ARG_LE: On entry, $x = 0.0$ and the function is infinite.

The evaluation has been abandoned due to the likelihood of overflow. The argument $x < - x_{hi}$ .

7 Accuracy

Unless stated otherwise, it is assumed that

x > 0

δ

and

ε

are the relative errors in argument and result respectively, then in principle,

|ε| ≃ |\frac{e^{- x}}{E_{1} (x)} \times δ|

so the relative error in the argument is amplified in the result by at least a factor

e^{- x} / E_{1} (x)

. The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is simply a result of round-off in the machine representation, it is possible that an extra figure may be lost in internal calculation and round-off.

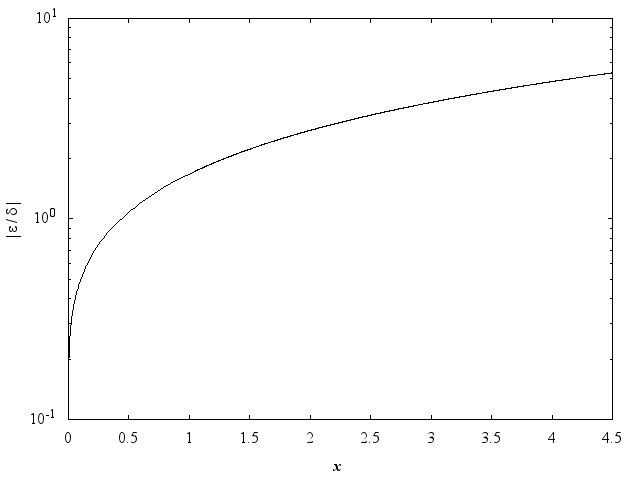
The behaviour of this amplification factor is shown in the following graph:

Figure 1

It should be noted that, for absolutely small

x

, the amplification factor tends to zero and eventually the error in the result will be limited by machine precision.

For absolutely large

x

ε \sim x δ = Δ,

the absolute error in the argument.

For

x < 0

, empirical tests have shown that the maximum relative error is a loss of approximately

1

decimal place.

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

The following program reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_exp_integral (s13aac)