NAG Library Function Document

nag_sinh (s10abc)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

▸▿ 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_sinh (s10abc) returns the value of the hyperbolic sine,

\sinh x

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_sinh (double x, NagError *fail)

3 Description

nag_sinh (s10abc) calculates an approximate value for the hyperbolic sine of its argument,

\sinh x

For

|x| \leq 1

it uses the Chebyshev expansion

\sinh x = x \times y (t) = x \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t)

where

t = 2 x^{2} - 1

For

1 < |x| \leq E_{1}, \sinh x = \frac{1}{2} (e^{x} - e^{- x})

where

E_{1}

is a machine-dependent constant, details of which are given in the Users' Note for your implementation.

For

|x| > E_{1}

, the function fails owing to the danger of setting overflow in calculating

e^{x}

. The result returned for such calls is

\sinh (sign x E_{1})

, i.e., it returns the result for the nearest valid argument.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Arguments

1: $x$ – doubleInput: On entry: the argument $x$ of the function.
2: $fail$ – NagError *Input/Output: The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_ALLOC_FAIL: Dynamic memory allocation failed.
See Section 3.2.1.2 in the Essential Introduction for further information.
NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.

An unexpected error has been triggered by this function. Please contact NAG.
See Section 3.6.6 in the Essential Introduction for further information.
NE_NO_LICENCE: Your licence key may have expired or may not have been installed correctly.
See Section 3.6.5 in the Essential Introduction for further information.
NE_REAL_ARG_GT: On entry, $x = 〈value〉$ .
Constraint: $|x| \leq E_{1}$ .
The function has been called with an argument too large in absolute magnitude. There is a danger of overflow. The result returned is the value of $\sinh x$ at the closest argument for which a valid call could be made.

7 Accuracy

δ

and

ε

are the relative errors in the argument and result, respectively, then in principle

|ε| ≃ |x \coth x \times δ| .

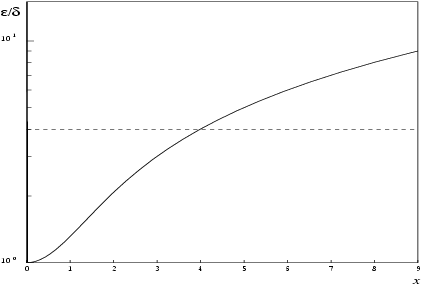
That is the relative error in the argument,

x

, is amplified by a factor, approximately

x \coth x

. The equality should hold if

δ

is greater than the machine precision (

δ

is a result of data errors etc.) but, if

δ

is simply a result of round-off in the machine representation of

x

, then it is possible that an extra figure may be lost in internal calculation round-off.

The behaviour of the error amplification factor can be seen in the following graph:

Figure 1

It should be noted that for

|x| \geq 2

ε \sim x δ = Δ

where

Δ

is the absolute error in the argument.

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_sinh (s10abc)

▸▿ Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

NAG Library Function Document

nag_sinh (s10abc)