NAG Library Function Document
nag_log_gamma (s14abc)
1 Purpose
nag_log_gamma (s14abc) returns the value of the logarithm of the gamma function, .
2 Specification
| #include <nag.h> |
| #include <nags.h> |
| double |
nag_log_gamma (double x,
NagError *fail) |
|
3 Description
nag_log_gamma (s14abc) calculates an approximate value for . It is based on rational Chebyshev expansions.
Denote by
a ratio of polynomials of degree
in the numerator and
in the denominator. Then:
- for ,
- for ,
- for ,
- for ,
- and for ,
For each expansion, the specific values of
and
are selected to be minimal such that the maximum relative error in the expansion is of the order
, where
is the maximum number of decimal digits that can be accurately represented for the particular implementation (see
nag_decimal_digits (X02BEC)).
Let
denote
machine precision and let
denote the largest positive model number (see
nag_real_largest_number (X02ALC)). For
the value
is not defined; nag_log_gamma (s14abc) returns zero and exits with
NE_REAL_ARG_LE. It also exits with
NE_REAL_ARG_LE when
, and in this case the value
is returned. For
in the interval
, the function
to machine accuracy.
Now denote by
the largest allowable argument for
on the machine. For
the
term in Equation
(1) is negligible. For
there is a danger of setting overflow, and so nag_log_gamma (s14abc) exits with
NE_REAL_ARG_GT and returns
. The value of
is given in the
Users' Note for your implementation.
4 References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Cody W J and Hillstrom K E (1967) Chebyshev approximations for the natural logarithm of the gamma function Math.Comp. 21 198–203
5 Arguments
- 1:
x – doubleInput
On entry: the argument of the function.
Constraint:
.
- 2:
fail – NagError *Input/Output
-
The NAG error argument (see
Section 3.6 in the Essential Introduction).
6 Error Indicators and Warnings
- NE_INTERNAL_ERROR
-
An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact
NAG for assistance.
- NE_REAL_ARG_GT
-
On entry, .
Constraint: .
- NE_REAL_ARG_LE
-
On entry, .
Constraint: .
7 Accuracy
Let and be the relative errors in the argument and result respectively, and be the absolute error in the result.
If
is somewhat larger than
machine precision, then
where
is the digamma function
.
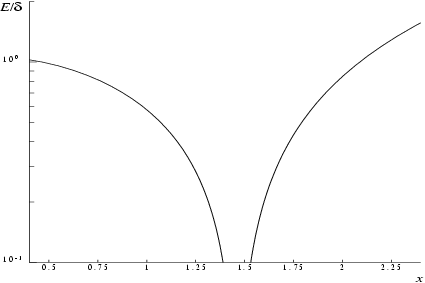
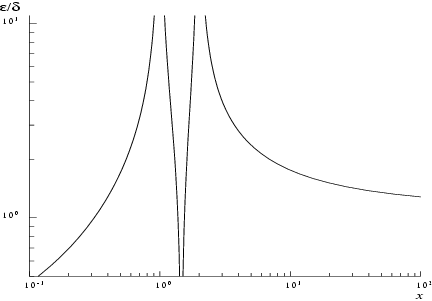
Figure 1 and
Figure 2 show the behaviour of these error amplification factors.
These show that relative error can be controlled, since except near relative error is attenuated by the function or at least is not greatly amplified.
For large , and for small , .
The function has zeros at and and hence relative accuracy is not maintainable near those points. However absolute accuracy can still be provided near those zeros as is shown above.
If however, is of the order of machine precision, then rounding errors in the function's internal arithmetic may result in errors which are slightly larger than those predicted by the equalities. It should be noted that even in areas where strong attenuation of errors is predicted the relative precision is bounded by the effective machine precision.
8 Parallelism and Performance
Not applicable.
None.
10 Example
This example reads values of the argument from a file, evaluates the function at each value of and prints the results.
10.1 Program Text
Program Text (s14abce.c)
10.2 Program Data
Program Data (s14abce.d)
10.3 Program Results
Program Results (s14abce.r)