NAG Library Function Document

nag_exp_integral (s13aac)

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

+− 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_exp_integral (s13aac) returns the value of the exponential integral

E_{1} (x)

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_exp_integral (double x, NagError *fail)

3 Description

nag_exp_integral (s13aac) calculates an approximate value for

E_{1} (x) = - Ei (- x) = \int_{x}^{\infty} \frac{e^{- u}}{u} d u .

using Chebyshev expansions, where

x

is real. For

x < 0

, the real part of the principal value of the integral is taken. The value

E_{1} (0)

is infinite, and so, when

x = 0

, nag_exp_integral (s13aac) exits with an error and returns the largest representable machine number.

For

0 < x \leq 4

E_{1} (x) = y (t) - \ln x = \underset{r}{\sum^{'}} a_{r} T_{r} (t) - \ln x,

where

t = \frac{1}{2} x - 1

For

x > 4

E_{1} (x) = \frac{e^{- x}}{x} y (t) = \frac{e^{- x}}{x} \underset{r}{\sum^{'}} a_{r} T_{r} (t),

where

t = - 1.0 + \frac{14.5}{(x + 3.25)} = \frac{11.25 - x}{3.25 + x}

In both cases,

- 1 \leq t \leq + 1

For

x < 0

, the approximation is based on expansions proposed by Cody and Thatcher Jr. (1969). Precautions are taken to maintain good relative accuracy in the vicinity of

x_{0} \approx - 0.372507 \dots

, which corresponds to a simple zero of Ei(

- x

nag_exp_integral (s13aac) guards against producing underflows and overflows by using the argument

x_{hi}

; see the Users' Note for your implementation for the value of

x_{hi}

. To guard against overflow, if

x < - x_{hi}

the function terminates and returns the negative of the largest representable machine number. To guard against underflow, if

x > x_{hi}

the result is set directly to zero.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Cody W J and Thatcher Jr. H C (1969) Rational Chebyshev approximations for the exponential integral Ei

(x)

Math. Comp. 23 289–303

5 Arguments

1: x – doubleInput: On entry: the argument $x$ of the function.
Constraint: $- x_{hi} \leq x < 0.0$ or $x > 0.0$ .
2: fail – NagError *Input/Output: The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
NE_REAL_ARG_LE: On entry, $x = 0.0$ and the function is infinite.
The evaluation has been abandoned due to the likelihood of overflow. The argument $x < - x_{hi}$ .

7 Accuracy

Unless stated otherwise, it is assumed that

x > 0

δ

and

ε

are the relative errors in argument and result respectively, then in principle,

|ε| ≃ |\frac{e^{- x}}{E_{1} (x)} \times δ|

so the relative error in the argument is amplified in the result by at least a factor

e^{- x} / E_{1} (x)

. The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is simply a result of round-off in the machine representation, it is possible that an extra figure may be lost in internal calculation and round-off.

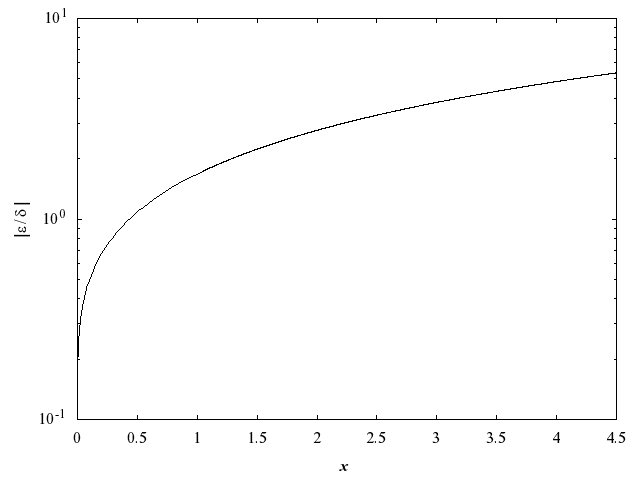
The behaviour of this amplification factor is shown in the following graph:

Figure 1

It should be noted that, for absolutely small

x

, the amplification factor tends to zero and eventually the error in the result will be limited by machine precision.

For absolutely large

x

ε \sim x δ = Δ,

the absolute error in the argument.

For

x < 0

, empirical tests have shown that the maximum relative error is a loss of approximately

1

decimal place.

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

The following program reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_exp_integral (s13aac)