NAG Library Function Document

nag_arcsinh (s11abc)

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

+− 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_arcsinh (s11abc) returns the value of the inverse hyperbolic sine,

arcsinh x

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_arcsinh (double x)

3 Description

nag_arcsinh (s11abc) calculates an approximate value for the inverse hyperbolic sine of its argument,

arcsinh x

For

|x| \leq 1

it is based on the Chebyshev expansion

arcsinh x = x \times y (t) = x \underset{r = 0}{\sum^{'}} c_{r} T_{r} (t),   where ​ t = 2 x^{2} - 1 .

For

|x| > 1

it uses the fact that

arcsinh x = sign x \times \ln (|x| + \sqrt{x^{2} + 1}) .

This form is used directly for

1 < |x| < 10^{k}

, where

k = n / 2 + 1

, and the machine uses approximately

n

decimal place arithmetic.

For

|x| \geq 10^{k}

\sqrt{x^{2} + 1}

is equal to

|x|

to within the accuracy of the machine and hence we can guard against premature overflow and, without loss of accuracy, calculate

arcsinh x = sign x \times (\ln 2 + \ln |x|) .

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Arguments

1: x – doubleInput: On entry: the argument $x$ of the function.

6 Error Indicators and Warnings

None.

7 Accuracy

δ

and

ε

are the relative errors in the argument and the result, respectively, then in principle

|ε| ≃ |\frac{x}{\sqrt{1 + x^{2}} arcsinh x} δ| .

That is, the relative error in the argument,

x

, is amplified by a factor at least

\frac{x}{\sqrt{1 + x^{2}} arcsinh x}

, in the result.

The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is simply due to round-off in the machine representation it is possible that an extra figure may be lost in internal calculation round-off.

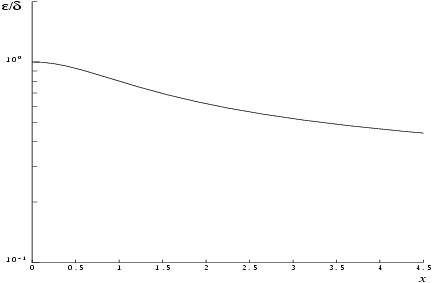
The behaviour of the amplification factor is shown in the following graph:

Figure 1

It should be noted that this factor is always less than or equal to one. For large

x

we have the absolute error in the result,

E

, in principle, given by

E \sim δ .

This means that eventually accuracy is limited by machine precision.

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_arcsinh (s11abc)