NAG Library Function Document

nag_cosh (s10acc)

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

+− 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_cosh (s10acc) returns the value of the hyperbolic cosine,

\cosh x

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_cosh (double x, NagError *fail)

3 Description

nag_cosh (s10acc) calculates an approximate value for the hyperbolic cosine,

\cosh x

For

|x| \leq E_{1}, \cosh x = \frac{1}{2} (e^{x} + e^{- x})

For

|x| > E_{1}

, the function fails owing to danger of setting overflow in calculating

e^{x}

. The result returned for such calls is

\cosh E_{1}

, i.e., it returns the result for the nearest valid argument. The value of machine-dependent constant

E_{1}

may be given in the Users' Note for your implementation.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Arguments

1: x – doubleInput: On entry: the argument $x$ of the function.
2: fail – NagError *Input/Output: The NAG error argument (see Section 3.6 in the Essential Introduction).

6 Error Indicators and Warnings

NE_INTERNAL_ERROR: An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact NAG for assistance.
NE_REAL_ARG_GT: On entry, $x = ⟨value⟩$ .
Constraint: $|x| \leq E_{1}$ .
The function has been called with an argument too large in absolute magnitude. There is a danger of overflow. The result returned is the value of $\cosh x$ at the nearest valid argument.

7 Accuracy

δ

and

ε

are the relative errors in the argument and result, respectively, then in principle

ε ≃ x \tanh x \times δ .

That is, the relative error in the argument,

x

, is amplified by a factor, at least

x \tanh x

. The equality should hold if

δ

is greater than the machine precision (

δ

is due to data errors etc.) but if

δ

is simply a result of round-off in the machine representation of

x

then it is possible that an extra figure may be lost in internal calculation round-off.

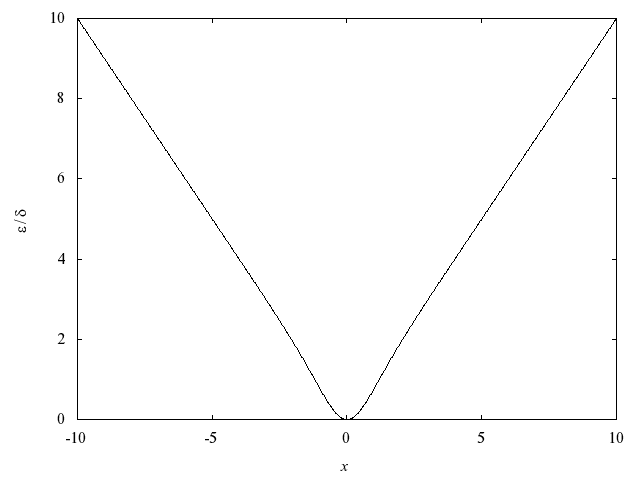
The behaviour of the error amplification factor is shown by the following graph:

Figure 1

It should be noted that near

x = 0

where this amplification factor tends to zero the accuracy will be limited eventually by the machine precision. Also for

|x| \geq 2

ε \sim x δ = Δ

where

Δ

is the absolute error in the argument

x

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_cosh (s10acc)