NAG Library Function Document

nag_tanh (s10aac)

+− Contents

1 Purpose

2 Specification

3 Description

4 References

5 Arguments

6 Error Indicators and Warnings

7 Accuracy

8 Parallelism and Performance

9 Further Comments

+− 10 Example

10.1 Program Text

10.2 Program Data

10.3 Program Results

1 Purpose

nag_tanh (s10aac) returns a value for the hyperbolic tangent,

\tanh x

2 Specification

#include <nag.h>

#include <nags.h>

double

nag_tanh (double x)

3 Description

nag_tanh (s10aac) calculates an approximate value for the hyperbolic tangent of its argument,

\tanh x

For

|x| \leq 1

it is based on the Chebyshev expansion

\tanh x = x \times y (t) = x \underset{r = 0}{\sum^{'}} a_{r} T_{r} (t)

where

- 1 \leq x \leq 1, - 1 \leq t \leq 1,   and t = 2 x^{2} - 1

For

1 < |x| < E_{1}

(see the Users' Note for your implementation for value of

E_{1}

)

\tanh x = \frac{e^{2 x} - 1}{e^{2 x} + 1} .

For

|x| \geq E_{1}

\tanh x = sign x

to within the representation accuracy of the machine and so this approximation is used.

4 References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

5 Arguments

1: x – doubleInput: On entry: the argument $x$ of the function.

6 Error Indicators and Warnings

None.

7 Accuracy

δ

and

ε

are the relative errors in the argument and the result respectively, then in principle,

|ε| ≃ |\frac{2 x}{\sinh 2 x} δ| .

That is, a relative error in the argument,

x

, is amplified by a factor approximately

\frac{2 x}{\sinh 2 x}

, in the result.

The equality should hold if

δ

is greater than the machine precision (

δ

due to data errors etc.) but if

δ

is due simply to the round-off in the machine representation it is possible that an extra figure may be lost in internal calculation round-off.

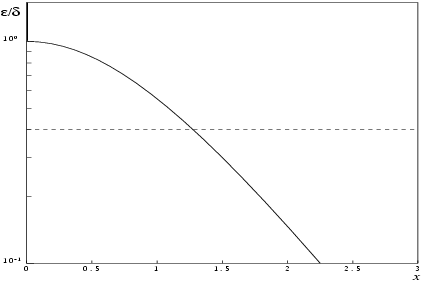
The behaviour of the amplification factor is shown in the following graph:

Figure 1

It should be noted that this factor is always less than or equal to

1.0

and away from

x = 0

the accuracy will eventually be limited entirely by the precision of machine representation.

8 Parallelism and Performance

Not applicable.

9 Further Comments

None.

10 Example

This example reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

NAG Library Function Documentnag_tanh (s10aac)