nag_lambertW_complex (c05bbc) calculates an approximate value for Lambert's
function (sometimes known as the ‘product log’ or ‘Omega’ function), which is the inverse function of
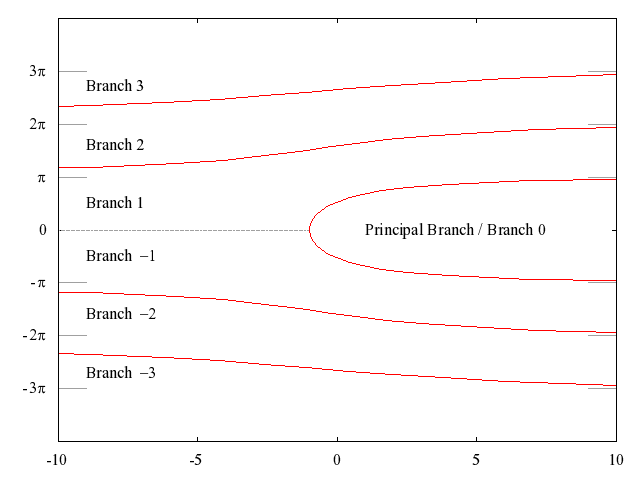
The function
is many-to-one, and so, except at
,
is multivalued. nag_lambertW_complex (c05bbc) allows you to specify the branch of
on which you would like the results to lie by using the argument
branch. Our choice of branch cuts is as in
Corless et al. (1996), and the ranges of the branches of
are summarised in
Figure 1.
For more information about the closure of each branch, which is not displayed in
Figure 1, see
Corless et al. (1996). The dotted lines in the Figure denote the asymptotic boundaries of the branches, at multiples of
.
The precise method used to approximate
is as described in
Corless et al. (1996). For
close to
greater accuracy comes from evaluating
rather than
: by setting
on entry you inform nag_lambertW_complex (c05bbc) that you are providing
, not
, in
z.
Corless R M, Gonnet G H, Hare D E G, Jeffrey D J and Knuth D
E (1996) On the Lambert function Advances in Comp. Math. 3 329–359
For a high percentage of
, nag_lambertW_complex (c05bbc) is accurate to the number of decimal digits of precision on the host machine (see
nag_decimal_digits (X02BEC)). An extra digit may be lost on some platforms and for a small proportion of
. This depends on the accuracy of the base-
logarithm on your system.
Not applicable.
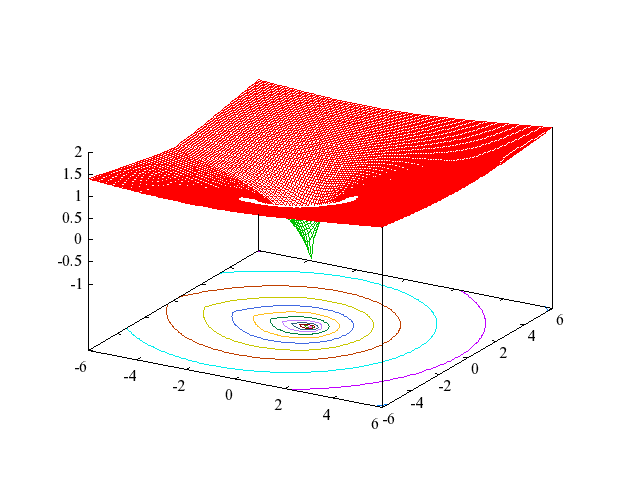
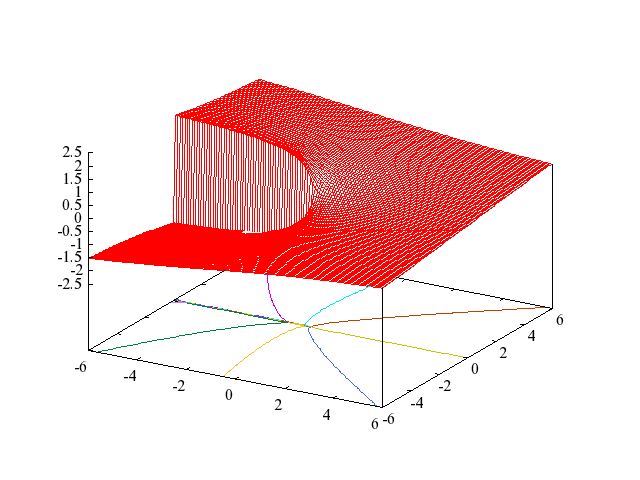
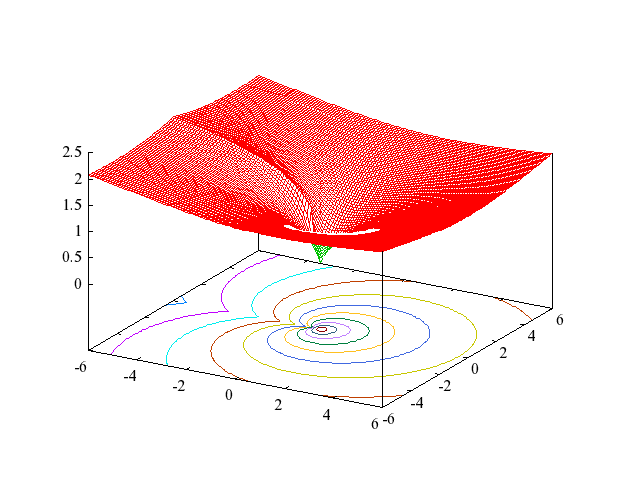
The following figures show the principal branch of
.
Figure 2:
Figure 3:
Figure 4:
This example reads from a file the value of the required branch, whether or not the arguments to are to be considered as offsets to , and the arguments themselves. It then evaluates the function for these sets of input data and prints the results.