| 1. | Set , and | ||
| 2. | Set . If , where is a user-supplied control parameter, then terminate the process for this segment. | ||
| 3. | Find that minimizes
|
||
| 4. | Test
|
||
| 5. | If inequality (1) is false then the process is terminated for this segment. | ||
| 6. | If inequality (1) is true, then is added to the set of change points, and the segment is split into two subsegments, and . The whole process is repeated from step 2 independently on each subsegment, with the relevant changes to the definition of and (i.e., is set to when processing the left hand subsegment and is set to when processing the right hand subsegment. |
Input Parameters
Output Parameters
Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.
Open in the MATLAB editor: g13ne_example
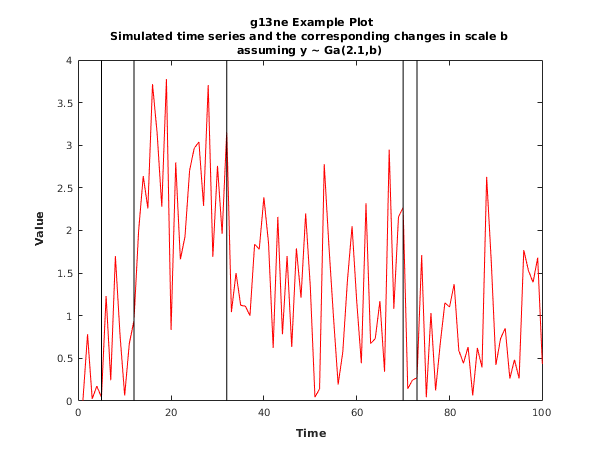
function g13ne_example fprintf('g13ne example results\n\n'); % Input series y = [ 0.00; 0.78; 0.02; 0.17; 0.04; 1.23; 0.24; 1.70; 0.77; 0.06; 0.67; 0.94; 1.99; 2.64; 2.26; 3.72; 3.14; 2.28; 3.78; 0.83; 2.80; 1.66; 1.93; 2.71; 2.97; 3.04; 2.29; 3.71; 1.69; 2.76; 1.96; 3.17; 1.04; 1.50; 1.12; 1.11; 1.00; 1.84; 1.78; 2.39; 1.85; 0.62; 2.16; 0.78; 1.70; 0.63; 1.79; 1.21; 2.20; 1.34; 0.04; 0.14; 2.78; 1.83; 0.98; 0.19; 0.57; 1.41; 2.05; 1.17; 0.44; 2.32; 0.67; 0.73; 1.17; 0.34; 2.95; 1.08; 2.16; 2.27; 0.14; 0.24; 0.27; 1.71; 0.04; 1.03; 0.12; 0.67; 1.15; 1.10; 1.37; 0.59; 0.44; 0.63; 0.06; 0.62; 0.39; 2.63; 1.63; 0.42; 0.73; 0.85; 0.26; 0.48; 0.26; 1.77; 1.53; 1.39; 1.68; 0.43]; % Shape parameter used in the cost function a = 2.1; % Length of the input series n = int64(numel(y)); % Need some persisteny workspace in the user function work = zeros(2*n,1); % The input series, workspace and shape parameter % constitute the information that needs to be passed to the % costfun, so pack them together into a cell array which will % get passed through the NAG function user = {y; a; work}; % Penalty term beta = 3.4; % Drop small regions minss = int64(3); [tau] = g13ne(n,beta,@chgpfn,'minss',minss,'user',user); % Print the results fprintf(' -- Change Points --\n'); fprintf(' Number Position\n'); fprintf(' =====================\n'); for i = 1:numel(tau) fprintf(' %4d %6d\n', i, tau(i)); end % Plot the results fig1 = figure; % Plot the original series plot(y,'Color','red'); % Mark the change points, drop the last one as it is always % at the end of the series xpos = transpose(double(tau(1:end-1))*ones(1,2)); ypos = diag(ylim)*ones(2,numel(tau)-1); line(xpos,ypos,'Color','black'); % Add labels and titles title({'{\bf g13ne Example Plot}', 'Simulated time series and the corresponding changes in scale b', 'assuming y ~ Ga(2.1,b)'}); xlabel('{\bf Time}'); ylabel('{\bf Value}'); function [v,cost,user,info] = chgpfn(side,u,w,minss,user,info) % Function to calculate a proposed change point and associated cost % The cost is based on the likelihood of the gamma distribution y = user{1}; a = user{2}; work = user{3}; % Calculate the first and last positions for potential change % points, conditional on the fact that each sub-segment must be % at least minss wide floc = u + minss - 1; lloc = w - minss; % In order to calculate the cost of having a change point at i, we % need to calculate C(y(floc:i)) and C(y(i+1:lloc)), where C(.) is % the cost function (based on the gamma distribution in this example). % Rather than calculate these values at each call to chgpfn we store % the values in work for later use % If side = 1 (i.e. we are working with a left hand sub-segment), % we already have C(y(floc:i)) for this value of floc, so only need % to calculate C(y(i+1:lloc)), similarly when side = 2 we only need % to calculate C(y(floc:i)) % When side = -1, we need the cost of the full segment, which we do % in a forwards manner (calculating C(y(floc:i)) in the process), so % when side = 0 we only need to calculate C(y(i:1:lloc)) % Get the intermediate costs ys = 0; dn = 0; if (side==0 | side==1) % work(2*i) = C(y(i+1:w)) for i = w:-1:floc + 1 dn = dn + 1; tmp = dn*a; ys = ys + y(i); work(2*i-2) = 2.0*tmp*(log(ys)-log(tmp)); end % make sure we return the updated values of work user = {y; a; work}; else % work(2*i-1) = C(y(u:i)) if (side==-1) li = w; else li = lloc; end for i = u:li dn = dn + 1; tmp = dn*a; ys = ys + y(i); work(2*i-1) = 2.0*tmp*(log(ys)-log(tmp)); end % make sure we return the updated values of work user = {y; a; work}; end v = int64(0); cost = zeros(3,1); if (side>=0) % Need to find a potential change point v = int64(0); cost(1) = 0; % Loop over all possible change point locations for i = floc:lloc this_cost = work(2*i-1) + work(2*i); if (this_cost<cost(1) | v==0) % Update the proposed change point location v = int64(i); cost(1) = this_cost; cost(2) = work(2*i-1); cost(3) = work(2*i); end end else % Need to calculate the cost for the full segment cost(1) = work(2*w-1); % No need to populate the rest of COST or V end % Set info nonzero to terminate execution for any reason info = int64(0);
g13ne example results
-- Change Points --
Number Position
=====================
1 5
2 12
3 32
4 70
5 73
6 100
