, be the ordered distinct failure times for the sample of observed failure/censored times, and let the number of observations in the sample that have not failed by time

t_{i}

n_{i}

. If a failure and a loss (censored observation) occur at the same time

t_{i}

, then the failure is treated as if it had occurred slightly before time

t_{i}

and the loss as if it had occurred slightly after

t_{i}

The Kaplan–Meier estimate of the survival probabilities is a step function which in the interval

t_{i}

t_{i + 1}

is given by

\hat{S} (t) = \prod_{j = 1}^{i} (\frac{n_{j} - d_{j}}{n_{j}}),

where

d_{j}

is the number of failures occurring at time

t_{j}

nag_surviv_kaplanmeier (g12aa) computes the Kaplan–Meier estimates and the corresponding estimates of the variances,

\hat{var} (\hat{S} (t))

, using Greenwood's formula,

\hat{var} (\hat{S} (t)) = \hat{S} {(t)}^{2} \sum_{j = 1}^{i} \frac{d_{j}}{n_{j} (n_{j} - d_{j})} .

References

Gross A J and Clark V A (1975) Survival Distributions: Reliability Applications in the Biomedical Sciences Wiley

Kalbfleisch J D and Prentice R L (1980) The Statistical Analysis of Failure Time Data Wiley

Parameters

Compulsory Input Parameters

1: $t (n)$ – double array

The failure and censored times; these need not be ordered.

2: $ic (n)$ – int64int32nag_int array

ic (i)

contains the censoring code of the

i

th observation, for

i = 1, 2, \dots, n

$ic (i) = 0$: The $i$ th observation is a failure time.
$ic (i) = 1$: The $i$ th observation is right-censored.

Constraint:

ic (i) = 0

1

, for

i = 1, 2, \dots, n

3: $freq$ – string (length ≥ 1)

Indicates whether frequencies are provided for each time point.

$freq ='F'$: Frequencies are provided for each failure and censored time.
$freq ='S'$: The failure and censored times are considered as single observations, i.e., a frequency of $1$ is assumed.

Constraint:

freq ='F'

'S'

4: $ifreq (:)$ – int64int32nag_int array

The dimension of the array ifreq must be at least

n

freq ='F'

and at least

1

freq ='S'

freq ='F'

ifreq (i)

must contain the frequency of the

i

th observation.

ifreq ='S'

, a frequency of

1

is assumed and ifreq is not referenced.

Constraint: if

freq ='F'

ifreq (i) \geq 0

, for

i = 1, 2, \dots, n

Optional Input Parameters

1: $n$ – int64int32nag_int scalar: Default: the dimension of the arrays ic, t. (An error is raised if these dimensions are not equal.)
The number of failure and censored times given in t.

Constraint: $n \geq 2$ .

Output Parameters

1: $nd$ – int64int32nag_int scalar: The number of distinct failure times, $n_{d}$ .
2: $tp (n)$ – double array: $tp (i)$ contains the $i$ th ordered distinct failure time, $t_{i}$ , for $i = 1, 2, \dots, n_{d}$ .
3: $p (n)$ – double array: $p (i)$ contains the Kaplan–Meier estimate of the survival probability, $\hat{S} (t)$ , for time $tp (i)$ , for $i = 1, 2, \dots, n_{d}$ .
4: $psig (n)$ – double array: $psig (i)$ contains an estimate of the standard deviation of $p (i)$ , for $i = 1, 2, \dots, n_{d}$ .
5: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$

On entry,

n < 2

$ifail = 2$

On entry,

freq \neq'F'

'S'

$ifail = 3$

On entry,

ic (i) \neq 0

1

, for some

i = 1, 2, \dots, n

$ifail = 4$

On entry,

freq ='F'

and

ifreq (i) < 0

, for some

i = 1, 2, \dots, n

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

The computations are believed to be stable.

Further Comments

If there are no censored observations,

\hat{S} (t)

reduces to the ordinary binomial estimate of the probability of survival at time

t

Example

The remission times for a set of

21

leukaemia patients at

18

distinct time points are read in and the Kaplan–Meier estimate computed and printed. For further details see page 242 of Gross and Clark (1975).

Open in the MATLAB editor: g12aa_example

function g12aa_example


fprintf('g12aa example results\n\n');

t  = [         6;  6;  7;  9; 10; 10; 11; 13; 16;
              17; 19; 20; 22; 23; 25; 32; 34; 35];
ic = [int64(1);  0;  0;  1;  0;  1;  1;  0;  0;
               1;  1;  1;  0;  0;  1;  1;  1;  1];

freq  = 'Frequencies';
ifreq = ones(numel(t),1,'int64');
ifreq(2)  = 3;
ifreq(16) = 2;

% Calculate Kaplan-Meier statistic
[nd, tp, p, psig, ifail] = g12aa( ...
                                  t, ic, freq, ifreq);

% Display the results
fprintf('  Time   Survival    Standard\n');
fprintf('        probability  deviation\n\n');
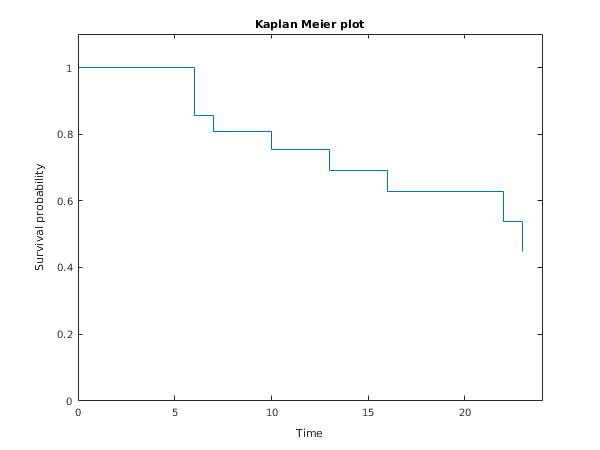
fprintf('%6.1f%10.3f%12.3f\n', [tp(1:nd) p(1:nd) psig(1:nd)]');

fig1 = figure;
stp = [0; tp(1:nd)];
sp  = [1; p(1:nd)];
stairs(stp,sp);
xlabel('Time');
ylabel('Survival probability');
title('Kaplan Meier plot');
legend('Off');
axis([0 tp(nd)+1 0 1.1]);

g12aa example results

  Time   Survival    Standard
        probability  deviation

   6.0     0.857       0.076
   7.0     0.807       0.087
  10.0     0.753       0.096
  13.0     0.690       0.107
  16.0     0.627       0.114
  22.0     0.538       0.128
  23.0     0.448       0.135

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox