hide long namesshow long names
hide short namesshow short names
Integer type:  int32  int64  nag_int  show int32  show int32  show int64  show int64  show nag_int  show nag_int
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox

NAG Toolbox: nag_smooth_data_runningmedian (g10ca)

▸▿ Contents

    1  Purpose
    2  Syntax
    3  Description
    4  References
▸▿ 5  Parameters
    6  Error Indicators and Warnings
    7  Accuracy
    8  Further Comments
    9  Example

Purpose

nag_smooth_data_runningmedian (g10ca) computes a smoothed data sequence using running median smoothers.

Syntax

[smooth, rough, ifail] = g10ca(itype, y, 'n', n)
[smooth, rough, ifail] = nag_smooth_data_runningmedian(itype, y, 'n', n)

Description

Given a sequence of n observations recorded at equally spaced intervals, nag_smooth_data_runningmedian (g10ca) fits a smooth curve through the data using one of two smoothers. The two smoothers are based on the use of running medians and averages to summarise overlapping segments. The fit and the residuals are called the smooth and the rough respectively. They obey the following:
Data=Smooth+Rough.  
The two smoothers are:
1. 4253H,twice consisting of a running median of 4, then 2, then 5, then 3 followed by hanning. Hanning is a running weighted average, the weights being 1/4, 1/2 and 1/4. The result of this smoothing is then reroughed by computing residuals, applying the same smoother to them and adding the result to the smooth of the first pass.
2. 3RSSH,twice consisting of a running median of 3, two splitting operations named S to improve the smooth sequence, each of which is followed by a running median of 3, and finally hanning. The end points are dealt with using the method described by Velleman and Hoaglin (1981). The full smoother 3RSSH,twice is produced by reroughing as described above.
The compound smoother 4253H,twice is recommended. The smoother 3RSSH,twice is popular when calculating by hand as it requires simpler computations and is included for comparison purposes.

References

Tukey J W (1977) Exploratory Data Analysis Addison–Wesley
Velleman P F and Hoaglin D C (1981) Applications, Basics, and Computing of Exploratory Data Analysis Duxbury Press, Boston, MA

Parameters

Compulsory Input Parameters

1:     itype – int64int32nag_int scalar
Specifies the method to be used.
  • If itype=0, 4253H,twice is used.
  • If itype=1, 3RSSH,twice is used.
Constraint: itype=0 or 1.
2:     yn – double array
The sample observations.

Optional Input Parameters

1:     n – int64int32nag_int scalar
Default: the dimension of the array y.
n, the number of observations.
Constraint: n>6.

Output Parameters

1:     smoothn – double array
Contains the smooth.
2:     roughn – double array
Contains the rough.
3:     ifail – int64int32nag_int scalar
ifail=0 unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:
   ifail=1
On entry,itype<0,
oritype>1.
   ifail=2
On entry,n≤6.
   ifail=-99
An unexpected error has been triggered by this routine. Please contact NAG.
   ifail=-399
Your licence key may have expired or may not have been installed correctly.
   ifail=-999
Dynamic memory allocation failed.

Accuracy

Not applicable.

Further Comments

Alternative methods of smoothing include the use of splines; see nag_smooth_fit_spline (g10ab) and nag_smooth_fit_spline_parest (g10ac).

Example

This example reads in a sequence of 49 observations on bituminous coal production (in millions of net tons per year) in the USA., 1920–1968 and is taken from Tukey (1977). For comparison purposes, both smoothers are applied to the data and the results are printed.

Open in the MATLAB editor: g10ca_example

function g10ca_example


fprintf('g10ca example results\n\n');

y = [569; 416; 422; 565; 484; 520; 573; 518; 501; 505;
     468; 382; 310; 334; 359; 372; 439; 446; 349; 395;
     461; 511; 583; 590; 620; 578; 534; 631; 600; 438;
     516; 534; 467; 457; 392; 467; 500; 493; 410; 412;
     416; 403; 422; 459; 467; 512; 534; 552; 545];

% Smooth sequence using 3RSSH,twice
itype = int64(1);
[smooth1, rough1, ifail] = g10ca( ...
                                  itype, y);

% Smooth sequence using 4253H,twice
itype = int64(0);
[smooth0, rough0, ifail] = g10ca( ...
                                  itype, y);

% Display results
fprintf('%39s%26s\n', 'Using 3RSSH,twice', 'Using 4253H,twice');
fprintf('%6s%9s%13s%13s%13s%13s\n', ' Index', '     Data', '      Smooth', ...
        '        Rough', '       Smooth', '       Rough');
ivar = [1:numel(y)]';
results = [ivar y smooth1 rough1 smooth0 rough0];
fprintf('%4d%11.1f%13.1f%13.1f%13.1f%13.1f\n', results');

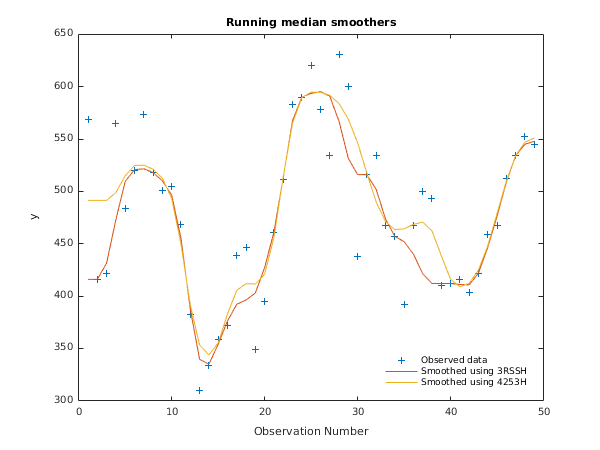
fig1 = figure;
plot(ivar,y,'+',ivar,smooth1,ivar,smooth0);
legend('Observed data', 'Smoothed using 3RSSH', 'Smoothed using 4253H', ...
       'Location', 'SouthEast');
legend('boxoff');
xlabel('Observation Number');
ylabel('y');
title('Running median smoothers');



g10ca example results

                      Using 3RSSH,twice         Using 4253H,twice
 Index     Data       Smooth        Rough       Smooth        Rough
   1      569.0        416.0        153.0        491.4         77.6
   2      416.0        416.0          0.0        491.4        -75.4
   3      422.0        431.5         -9.5        491.4        -69.4
   4      565.0        473.0         92.0        498.9         66.1
   5      484.0        509.5        -25.5        514.9        -30.9
   6      520.0        520.7         -0.7        524.7         -4.7
   7      573.0        521.6         51.4        525.0         48.0
   8      518.0        518.0          0.0        521.2         -3.2
   9      501.0        510.0         -9.0        512.6        -11.6
  10      505.0        496.5          8.5        493.2         11.8
  11      468.0        455.2         12.8        449.7         18.3
  12      382.0        387.5         -5.5        391.6         -9.6
  13      310.0        339.8        -29.8        353.4        -43.4
  14      334.0        334.9         -0.9        343.8         -9.8
  15      359.0        353.9          5.1        355.2          3.8
  16      372.0        376.1         -4.1        382.8        -10.8
  17      439.0        392.2         46.8        405.5         33.5
  18      446.0        396.2         49.8        411.9         34.1
  19      349.0        403.0        -54.0        411.6        -62.6
  20      395.0        427.2        -32.2        420.9        -25.9
  21      461.0        461.4         -0.4        456.1          4.9
  22      511.0        513.3         -2.3        513.9         -2.9
  23      583.0        567.6         15.4        565.2         17.8
  24      590.0        590.0          0.0        589.5          0.5
  25      620.0        593.5         26.5        594.7         25.3
  26      578.0        595.2        -17.2        594.6        -16.6
  27      534.0        590.9        -56.9        591.8        -57.8
  28      631.0        566.8         64.2        583.8         47.2
  29      600.0        531.5         68.5        569.0         31.0
  30      438.0        516.0        -78.0        546.3       -108.3
  31      516.0        516.0          0.0        517.3         -1.3
  32      534.0        501.9         32.1        489.6         44.4
  33      467.0        473.6         -6.6        471.2         -4.2
  34      457.0        457.0          0.0        463.5         -6.5
  35      392.0        452.0        -60.0        464.2        -72.2
  36      467.0        440.1         26.9        468.5         -1.5
  37      500.0        421.4         78.6        470.6         29.4
  38      493.0        412.0         81.0        462.3         30.7
  39      410.0        412.0         -2.0        438.6        -28.6
  40      412.0        412.0          0.0        416.1         -4.1
  41      416.0        411.1          4.9        408.9          7.1
  42      403.0        410.7         -7.7        412.2         -9.2
  43      422.0        422.0          0.0        424.9         -2.9
  44      459.0        446.6         12.4        448.1         10.9
  45      467.0        476.4         -9.4        478.8        -11.8
  46      512.0        509.0          3.0        510.0          2.0
  47      534.0        534.0          0.0        534.1         -0.1
  48      552.0        545.0          7.0        547.0          5.0
  49      545.0        547.8         -2.8        550.9         -5.9
g10ca_fig1.png
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015