PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_smooth_kerndens_gauss (g10bb)
Purpose
nag_smooth_kerndens_gauss2 (g10bb) performs kernel density estimation using a Gaussian kernel.
Syntax
[
window,
slo,
shi,
smooth,
t,
rcomm,
ifail] = g10bb(
x,
fcall,
rcomm, 'n',
n, 'wtype',
wtype, 'window',
window, 'slo',
slo, 'shi',
shi, 'ns',
ns)
[
window,
slo,
shi,
smooth,
t,
rcomm,
ifail] = nag_smooth_kerndens_gauss(
x,
fcall,
rcomm, 'n',
n, 'wtype',
wtype, 'window',
window, 'slo',
slo, 'shi',
shi, 'ns',
ns)
Description
Given a sample of
observations,
, from a distribution with unknown density function,
, an estimate of the density function,
, may be required. The simplest form of density estimator is the histogram. This may be defined by:
where
is the number of observations falling in the interval
to
,
is the lower bound to the histogram,
is the upper bound and
is the total number of intervals. The value
is known as the window width. To produce a smoother density estimate a kernel method can be used. A kernel function,
, satisfies the conditions:
The kernel density estimator is then defined as
The choice of
is usually not important but to ease the computational burden use can be made of the Gaussian kernel defined as
The smoothness of the estimator depends on the window width
. The larger the value of
the smoother the density estimate. The value of
can be chosen by examining plots of the smoothed density for different values of
or by using cross-validation methods (see
Silverman (1990)).
Silverman (1982) and
Silverman (1990) show how the Gaussian kernel density estimator can be computed using a fast Fourier transform (FFT). In order to compute the kernel density estimate over the range
to
the following steps are required.
| (i) |
Discretize the data to give equally spaced points with weights (see Jones and Lotwick (1984)). |
| (ii) |
Compute the FFT of the weights to give . |
| (iii) |
Compute where . |
| (iv) |
Find the inverse FFT of to give . |
To compute the kernel density estimate for further values of
only steps
(iii) and
(iv) need be repeated.
References
Jones M C and Lotwick H W (1984) Remark AS R50. A remark on algorithm AS 176. Kernel density estimation using the Fast Fourier Transform Appl. Statist. 33 120–122
Silverman B W (1982) Algorithm AS 176. Kernel density estimation using the fast Fourier transform Appl. Statist. 31 93–99
Silverman B W (1990) Density Estimation Chapman and Hall
Parameters
Compulsory Input Parameters
- 1:
– double array
-
, for
.
If
,
x must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
- 2:
– int64int32nag_int scalar
-
If
then the values of
are to be calculated by this call to
nag_smooth_kerndens_gauss2 (g10bb), otherwise it is assumed that the values of
were calculated by a previous call to this routine and the relevant information is stored in
rcomm.
Constraint:
or .
- 3:
– double array
-
Communication array, used to store information between calls to
nag_smooth_kerndens_gauss2 (g10bb).
If
,
rcomm must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
x.
, the number of observations in the sample.
If
,
n must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
Constraint:
.
- 2:
– int64int32nag_int scalar
Suggested value:
and .
Default:
How the window width,
, is to be calculated:
- is supplied in window.
- is to be calculated from the data, with
where is the inter-quartile range and the standard deviation of the sample, , and is a multipler supplied in window. The and quartiles, and , are calculated using nag_stat_quantiles (g01am). This is the "rule-of-thumb" suggested by Silverman (1990).
Constraint:
or .
- 3:
– double scalar
Suggested value:
and .
Default:
If , then , the window width. Otherwise, , the multiplier used in the calculation of .
Constraint:
.
- 4:
– double scalar
Suggested value:
and which would cause and to be set window widths below and above the lowest and highest data points respectively.
Default:
If
then
, the lower limit of the interval on which the estimate is calculated. Otherwise,
and
, the lower and upper limits of the interval, are calculated as follows:
where
is the window width.
For most applications should be at least three window widths below the lowest data point.
If
,
slo must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
- 5:
– double scalar
Default:
If
then
, the upper limit of the interval on which the estimate is calculated. Otherwise a value for
is calculated from the data as stated in the description of
slo and the value supplied in
shi is not used.
For most applications should be at least three window widths above the highest data point.
If
,
shi must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
- 6:
– int64int32nag_int scalar
Default:
, the number of points at which the estimate is calculated.
If
,
ns must be unchanged since the last call to
nag_smooth_kerndens_gauss2 (g10bb).
Constraints:
- ;
- The largest prime factor of ns must not exceed , and the total number of prime factors of ns, counting repetitions, must not exceed .
Output Parameters
- 1:
– double scalar
Suggested value:
and .
Default:
, the window width actually used.
- 2:
– double scalar
Suggested value:
and which would cause and to be set window widths below and above the lowest and highest data points respectively.
Default:
, the lower limit actually used.
- 3:
– double scalar
Default:
, the upper limit actually used.
- 4:
– double array
-
, for , the values of the density estimate.
- 5:
– double array
-
, for , the points at which the estimate is calculated.
- 6:
– double array
-
The last
ns elements of
rcomm contain the fast Fourier transform of the weights of the discretized data, that is
, for
.
- 7:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Note: nag_smooth_kerndens_gauss2 (g10bb) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
Constraint: .
-
-
Constraint: if
,
n must be unchanged since previous call.
-
-
Constraint: or .
-
-
Constraint: .
-
-
Constraint: if
,
slo must be unchanged since previous call.
- W
-
slo is not at least three window widths below the lowest data point or
shi is not at least three window widths above the highest data point. All output values have been returned.
-
-
Constraint: if
,
shi must be unchanged since previous call.
-
-
Constraint: .
-
-
Constraint: largest prime factor of
ns must not exceed
.
-
-
Constraint: total number of prime factors of
ns must not exceed
.
-
-
Constraint: if
,
ns must be unchanged since previous call.
-
-
Constraint: or .
-
-
rcomm has been corrupted between calls.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
See
Jones and Lotwick (1984) for a discussion of the accuracy of this method.
Further Comments
The time for computing the weights of the discretized data is of order , while the time for computing the FFT is of order , as is the time for computing the inverse of the FFT.
Example
Data is read from a file and the density estimated. The first values are then printed.
Open in the MATLAB editor:
g10bb_example
function g10bb_example
fprintf('g10bb example results\n\n');
x = [ 0.114 -0.232 -0.570 1.853 -0.994 ...
-0.374 -1.028 0.509 0.881 -0.453 ...
0.588 -0.625 -1.622 -0.567 0.421 ...
-0.475 0.054 0.817 1.015 0.608 ...
-1.353 -0.912 -1.136 1.067 0.121 ...
-0.075 -0.745 1.217 -1.058 -0.894 ...
1.026 -0.967 -1.065 0.513 0.969 ...
0.582 -0.985 0.097 0.416 -0.514 ...
0.898 -0.154 0.617 -0.436 -1.212 ...
-1.571 0.210 -1.101 1.018 -1.702 ...
-2.230 -0.648 -0.350 0.446 -2.667 ...
0.094 -0.380 -2.852 -0.888 -1.481 ...
-0.359 -0.554 1.531 0.052 -1.715 ...
1.255 -0.540 0.362 -0.654 -0.272 ...
-1.810 0.269 -1.918 0.001 1.240 ...
-0.368 -0.647 -2.282 0.498 0.001 ...
-3.059 -1.171 0.566 0.948 0.925 ...
0.825 0.130 0.930 0.523 0.443 ...
-0.649 0.554 -2.823 0.158 -1.180 ...
0.610 0.877 0.791 -0.078 1.412];
wtype = int64(2);
fcall = int64(1);
ns = 512;
rcomm = zeros(ns+20,1);
[window, slo, shi, smooth, t, rcomm, ifail] = ...
g10bb( ...
x, fcall, rcomm, 'wtype',wtype);
fprintf('Window Width Used = %11.4e\n', window);
fprintf('Interval = (%11.4e,%11.4e)\n\n', slo, shi);
fprintf('First %2d output values:\n\n',20);
fprintf(' Time point Density estimate\n');
fprintf(' ---------- ----------------\n');
fprintf(' %13.4f %13.4e\n', [t(1:20), smooth(1:20)]')
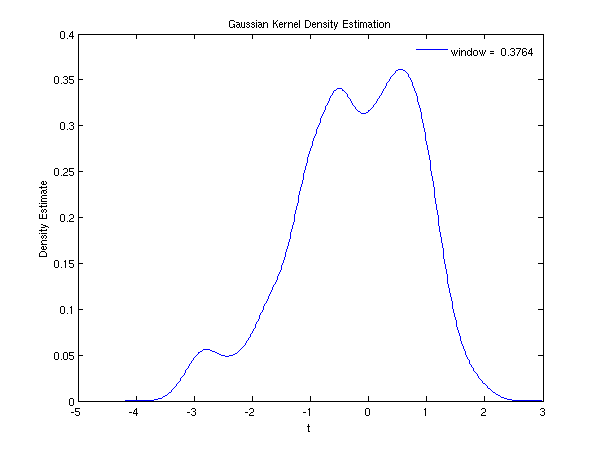
fig1 = figure;
plot(t,smooth);
title('Gaussian Kernel Density Estimation');
xlabel('t');
ylabel('Density Estimate');
wind_leg = sprintf('window = %7.4f',window);
legend(wind_leg);
legend('boxoff');
g10bb example results
Window Width Used = 3.7638e-01
Interval = (-4.1882e+00, 2.9822e+00)
First 20 output values:
Time point Density estimate
---------- ----------------
-4.1811 3.8281e-06
-4.1671 4.0305e-06
-4.1531 4.4233e-06
-4.1391 5.0212e-06
-4.1251 5.8461e-06
-4.1111 6.9279e-06
-4.0971 8.3048e-06
-4.0831 1.0025e-05
-4.0691 1.2145e-05
-4.0551 1.4736e-05
-4.0411 1.7881e-05
-4.0271 2.1677e-05
-4.0131 2.6239e-05
-3.9991 3.1700e-05
-3.9851 3.8214e-05
-3.9711 4.5960e-05
-3.9571 5.5141e-05
-3.9431 6.5990e-05
-3.9291 7.8775e-05
-3.9151 9.3796e-05
This plot shows the estimated density function for the example data for several window widths.
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015