Note: this function is scheduled to be withdrawn, please see
g10ba in
Advice on Replacement Calls for Withdrawn/Superseded Routines..
Given a sample of
observations,
, from a distribution with unknown density function,
, an estimate of the density function,
, may be required. The simplest form of density estimator is the histogram. This may be defined by:
where
is the number of observations falling in the interval
to
,
is the lower bound to the histogram and
is the upper bound. The value
is known as the window width. To produce a smoother density estimate a kernel method can be used. A kernel function,
, satisfies the conditions:
The kernel density estimator is then defined as
The choice of
is usually not important but to ease the computational burden use can be made of the Gaussian kernel defined as
The smoothness of the estimator depends on the window width
. The larger the value of
the smoother the density estimate. The value of
can be chosen by examining plots of the smoothed density for different values of
or by using cross-validation methods (see
Silverman (1990)).
Silverman (1982) and
Silverman (1990) show how the Gaussian kernel density estimator can be computed using a fast Fourier transform (
fft). In order to compute the kernel density estimate over the range
to
the following steps are required.
| (i) |
Discretize the data to give equally spaced points with weights (see Jones and Lotwick (1984)). |
| (ii) |
Compute the fft of the weights to give . |
| (iii) |
Compute where . |
| (iv) |
Find the inverse fft of to give . |
To compute the kernel density estimate for further values of
only steps
(iii) and
(iv) need be repeated.
Jones M C and Lotwick H W (1984) Remark AS R50. A remark on algorithm AS 176. Kernel density estimation using the Fast Fourier Transform Appl. Statist. 33 120–122
Silverman B W (1982) Algorithm AS 176. Kernel density estimation using the fast Fourier transform Appl. Statist. 31 93–99
See
Jones and Lotwick (1984) for a discussion of the accuracy of this method.
The time for computing the weights of the discretized data is of order
, while the time for computing the
fft is of order
, as is the time for computing the inverse of the
fft.
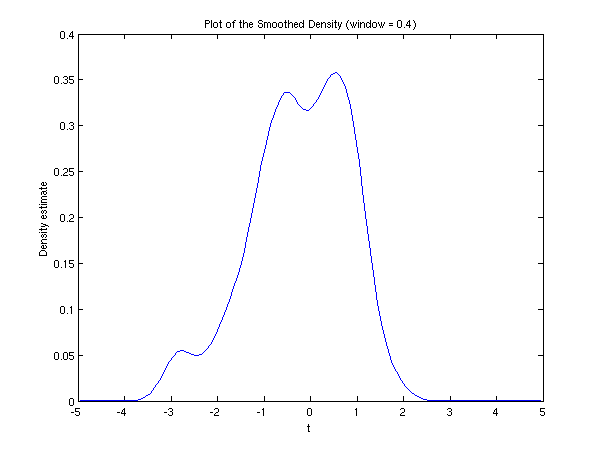
Data is read from a file and the density estimated. The first values are then printed. The full estimated density function is shown in the accompanying plot.
function g10ba_example
fprintf('g10ba example results\n\n');
x = [ 0.114 -0.232 -0.570 1.853 -0.994 ...
-0.374 -1.028 0.509 0.881 -0.453 ...
0.588 -0.625 -1.622 -0.567 0.421 ...
-0.475 0.054 0.817 1.015 0.608 ...
-1.353 -0.912 -1.136 1.067 0.121 ...
-0.075 -0.745 1.217 -1.058 -0.894 ...
1.026 -0.967 -1.065 0.513 0.969 ...
0.582 -0.985 0.097 0.416 -0.514 ...
0.898 -0.154 0.617 -0.436 -1.212 ...
-1.571 0.210 -1.101 1.018 -1.702 ...
-2.230 -0.648 -0.350 0.446 -2.667 ...
0.094 -0.380 -2.852 -0.888 -1.481 ...
-0.359 -0.554 1.531 0.052 -1.715 ...
1.255 -0.540 0.362 -0.654 -0.272 ...
-1.810 0.269 -1.918 0.001 1.240 ...
-0.368 -0.647 -2.282 0.498 0.001 ...
-3.059 -1.171 0.566 0.948 0.925 ...
0.825 0.130 0.930 0.523 0.443 ...
-0.649 0.554 -2.823 0.158 -1.180 ...
0.610 0.877 0.791 -0.078 1.412 ];
window = 0.4;
slo = -5;
shi = 5;
usefft = false;
fft = zeros(100,1);
[smooth, t, fft, ifail] = g10ba( ...
x, window, slo, shi, usefft, fft);
fprintf('Window Width Used = %11.4e\n', window);
fprintf('Interval = (%11.4e, %11.4e)\n\n', slo, shi);
fprintf('First 20 output values:\n\n');
fprintf(' Time Density\n');
fprintf(' Point Estimate\n');
fprintf(' ---------------------------\n');
fprintf('%13.3e%13.3e\n', [t(1:20), smooth(1:20)]');
fig1 = figure;
plot(t,smooth);
title('Plot of the Smoothed Density (window = 0.4)');
xlabel('t');
ylabel('Density estimate');
set(gca, 'XTick', [-5:5]);