PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_rand_field_2d_predef_setup (g05zr)
Purpose
nag_rand_field_2d_predef_setup (g05zr) performs the setup required in order to simulate stationary Gaussian random fields in two dimensions, for a preset variogram, using the
circulant embedding method. Specifically, the eigenvalues of the extended covariance matrix (or embedding matrix) are calculated, and their square roots output, for use by
nag_rand_field_2d_generate (g05zs), which simulates the random field.
Syntax
[
lam,
xx,
yy,
m,
approx,
rho,
icount,
eig,
ifail] = g05zr(
ns,
xmin,
xmax,
ymin,
ymax,
maxm,
var,
icov2,
params, 'norm_p',
norm_p, 'np',
np, 'pad',
pad, 'icorr',
icorr)
[
lam,
xx,
yy,
m,
approx,
rho,
icount,
eig,
ifail] = nag_rand_field_2d_predef_setup(
ns,
xmin,
xmax,
ymin,
ymax,
maxm,
var,
icov2,
params, 'norm_p',
norm_p, 'np',
np, 'pad',
pad, 'icorr',
icorr)
Description
A two-dimensional random field in is a function which is random at every point , so is a random variable for each . The random field has a mean function and a symmetric positive semidefinite covariance function . is a Gaussian random field if for any choice of and , the random vector follows a multivariate Normal distribution, which would have a mean vector with entries and a covariance matrix with entries . A Gaussian random field is stationary if is constant for all and for all and hence we can express the covariance function as a function of one variable: . is known as a variogram (or more correctly, a semivariogram) and includes the multiplicative factor representing the variance such that .
The functions
nag_rand_field_2d_predef_setup (g05zr) and
nag_rand_field_2d_generate (g05zs) are used to simulate a two-dimensional stationary Gaussian random field, with mean function zero and variogram
, over a domain
, using an equally spaced set of
points;
points in the
-direction and
points in the
-direction. The problem reduces to sampling a Gaussian random vector
of size
, with mean vector zero and a symmetric covariance matrix
, which is an
by
block Toeplitz matrix with Toeplitz blocks of size
by
. Since
is in general expensive to factorize, a technique known as the
circulant embedding method is used.
is embedded into a larger, symmetric matrix
, which is an
by
block circulant matrix with circulant blocks of size
by
, where
and
.
can now be factorized as
, where
is the two-dimensional Fourier matrix (
is the complex conjugate of
),
is the diagonal matrix containing the eigenvalues of
and
.
is known as the embedding matrix. The eigenvalues can be calculated by performing a discrete Fourier transform of the first row (or column) of
and multiplying by
, and so only the first row (or column) of
is needed – the whole matrix does not need to be formed.
As long as all of the values of are non-negative (i.e., is positive semidefinite), is a covariance matrix for a random vector which has blocks of size . Two samples of can now be simulated from the real and imaginary parts of , where and have elements from the standard Normal distribution. Since , this calculation can be done using a discrete Fourier transform of the vector . Two samples of the random vector can now be recovered by taking the first elements of the first blocks of each sample of – because the original covariance matrix is embedded in , will have the correct distribution.
If
is not positive semidefinite, larger embedding matrices
can be tried; however if the size of the matrix would have to be larger than
maxm, an approximation procedure is used. We write
, where
and
contain the non-negative and negative eigenvalues of
respectively. Then
is replaced by
where
and
is a scaling factor. The error
in approximating the distribution of the random field is given by
Three choices for
are available, and are determined by the input argument
icorr:
- setting sets
- setting sets
- setting sets .
nag_rand_field_2d_predef_setup (g05zr) finds a suitable positive semidefinite embedding matrix
and outputs its sizes in the vector
m and the square roots of its eigenvalues in
lam. If approximation is used, information regarding the accuracy of the approximation is output. Note that only the first row (or column) of
is actually formed and stored.
References
Dietrich C R and Newsam G N (1997) Fast and exact simulation of stationary Gaussian processes through circulant embedding of the covariance matrix SIAM J. Sci. Comput. 18 1088–1107
Schlather M (1999) Introduction to positive definite functions and to unconditional simulation of random fields Technical Report ST 99–10 Lancaster University
Wood A T A and Chan G (1997) Algorithm AS 312: An Algorithm for Simulating Stationary Gaussian Random Fields Journal of the Royal Statistical Society, Series C (Applied Statistics) (Volume 46) 1 171–181
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int array
-
The number of sample points to use in each direction, with sample points in the -direction, and sample points in the -direction, . The total number of sample points on the grid is therefore .
- 2:
– double scalar
-
The lower bound for the -coordinate, for the region in which the random field is to be simulated.
Constraint:
.
- 3:
– double scalar
-
The upper bound for the -coordinate, for the region in which the random field is to be simulated.
Constraint:
.
- 4:
– double scalar
-
The lower bound for the -coordinate, for the region in which the random field is to be simulated.
Constraint:
.
- 5:
– double scalar
-
The upper bound for the -coordinate, for the region in which the random field is to be simulated.
Constraint:
.
- 6:
– int64int32nag_int array
-
Determines the maximum size of the circulant matrix to use – a maximum of elements in the -direction, and a maximum of elements in the -direction. The maximum size of the circulant matrix is thus .
Constraint:
, where is the smallest integer satisfying , for .
- 7:
– double scalar
-
The multiplicative factor of the variogram .
Constraint:
.
- 8:
– int64int32nag_int scalar
-
Determines which of the preset variograms to use. The choices are given below. Note that
, where
and
are correlation lengths in the
and
directions respectively and are parameters for most of the variograms, and
is the variance specified by
var.
- Symmetric stable variogram
where
- , ,
- , ,
- , .
- Cauchy variogram
where
- , ,
- , ,
- , .
- Differential variogram with compact support
where
- , ,
- , .
- Exponential variogram
where
- , ,
- , .
- Gaussian variogram
where
- , ,
- , .
- Nugget variogram
No parameters need be set for this value of icov2.
- Spherical variogram
where
- , ,
- , .
- Bessel variogram
where
- is the Bessel function of the first kind,
- , ,
- , ,
- , .
- Hole effect variogram
where
- , ,
- , .
- Whittle-Matérn variogram
where
- is the modified Bessel function of the second kind,
- , ,
- , ,
- , .
- Continuously parameterised variogram with compact support
where
- ,
- is the modified Bessel function of the second kind,
- , ,
- , ,
- , ,
- , ,
- , .
- Generalized hyperbolic distribution variogram
where
- is the modified Bessel function of the second kind,
- , ,
- , ,
- , no constraint on ,
- , ,
- , .
Constraint:
, , , , , , , , , , or .
- 9:
– double array
-
The parameters for the variogram as detailed in the description of
icov2.
Constraint:
see
icov2 for a description of the individual parameter constraints.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
Default:
Determines which norm to use when calculating the variogram.
- The 1-norm is used, i.e., .
- The 2-norm (Euclidean norm) is used, i.e., .
Constraint:
or .
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
params.
The number of parameters to be set. Different covariance functions need a different number of parameters.
- np must be set to .
- , , , or
- np must be set to .
- , , or
- np must be set to .
- or
- np must be set to .
- 3:
– int64int32nag_int scalar
Default:
Determines whether the embedding matrix is padded with zeros, or padded with values of the variogram. The choice of padding may affect how big the embedding matrix must be in order to be positive semidefinite.
- The embedding matrix is padded with zeros.
- The embedding matrix is padded with values of the variogram.
Constraint:
or .
- 4:
– int64int32nag_int scalar
Default:
Determines which approximation to implement if required, as described in
Description.
Constraint:
, or .
Output Parameters
- 1:
– double array
-
Contains the square roots of the eigenvalues of the embedding matrix.
- 2:
– double array
-
The points of the -coordinates at which values of the random field will be output.
- 3:
– double array
-
The points of the -coordinates at which values of the random field will be output.
- 4:
– int64int32nag_int array
-
contains , the size of the circulant blocks and contains , the number of blocks, resulting in a final square matrix of size .
- 5:
– int64int32nag_int scalar
-
Indicates whether approximation was used.
- No approximation was used.
- Approximation was used.
- 6:
– double scalar
-
Indicates the scaling of the covariance matrix. unless approximation was used with or .
- 7:
– int64int32nag_int scalar
-
Indicates the number of negative eigenvalues in the embedding matrix which have had to be set to zero.
- 8:
– double array
-
Indicates information about the negative eigenvalues in the embedding matrix which have had to be set to zero. contains the smallest eigenvalue, contains the sum of the squares of the negative eigenvalues, and contains the sum of the absolute values of the negative eigenvalues.
- 9:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
Constraint: , .
-
-
Constraint: .
-
-
Constraint: .
-
-
Constraint: the minimum calculated value for
maxm are
.
Where the minima of
is given by
, where
is the smallest integer satisfying
, for
.
-
-
Constraint: .
-
-
Constraint: and .
-
-
Constraint: or .
-
-
Constraint: for , .
-
-
Constraint: dependent on
icov2, see documentation.
-
-
Constraint: or .
-
-
Constraint: , or .
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
If on exit
, see the comments in
Description regarding the quality of approximation; increase the values in
maxm to attempt to avoid approximation.
Further Comments
None.
Example
This example calls nag_rand_field_2d_predef_setup (g05zr) to calculate the eigenvalues of the embedding matrix for sample points on a by grid of a two-dimensional random field characterized by the symmetric stable variogram ().
Open in the MATLAB editor:
g05zr_example
function g05zr_example
fprintf('g05zr example results\n\n');
icov2 = int64(1);
params = [0.1; 0.15; 1.2];
var = 0.5;
xmin = -1;
xmax = 1;
ymin = -0.5;
ymax = 0.5;
ns = [int64(5), 5];
maxm = [int64(64), 64];
icorr = int64(2);
[lam, xx, yy, m, approx, rho, icount, eig, ifail] = ...
g05zr( ...
ns, xmin, xmax, ymin, ymax, maxm, var, ...
icov2, params, 'icorr', icorr);
fprintf('Size of embedding matrix = %d\n\n', m(1)*m(2));
if approx == 1
fprintf('Approximation required\n\n');
fprintf('rho = %10.5f\n', rho);
fprintf('eig = %10.5f%10.5f%10.5f\n', eig(1:3));
fprintf('icount = %d\n', icount);
else
fprintf('Approximation not required\n\n');
end
fprintf('Square roots of eigenvalues of embedding matrix:\n');
mlam = reshape(lam(1:m(1)*m(2)), m(1), m(2));
for i = 1:m(1)
fprintf('%8.4f',mlam(i,:));
fprintf('\n');
end
g05zr_plot;
function g05zr_plot
icov2 = int64(4);
params = [0.1; 0.1];
var = 1;
xmin = 0;
xmax = 1;
ymin = 0;
ymax = 1;
ns = [int64(100), 100];
maxm = [int64(4096), 4096];
icorr = int64(0);
[lam, xx, yy, m, approx, rho, icount, eig, ifail] = ...
g05zr( ...
ns, xmin, xmax, ymin, ymax, maxm, var, ...
icov2, params);
genid = int64(1);
subid = int64(1);
seed = [int64(14965)];
[state, ifail] = g05kf( ...
genid, subid, seed);
s = int64(2);
[state, z, ifail] = g05zs( ...
ns, s, m, lam, rho, state);
fig1 = figure;
zz = reshape(z(:,1),[100,100]);
contourf(xx,yy,zz);
axis equal;
title({'First realization of Random Field', ...
'exponential variogram, corr. length = 0.1'});
fig2 = figure;
zz = reshape(z(:,2),[100,100]);
contourf(xx,yy,zz);
axis equal;
title({'Second realization of Random Field', ...
'exponential variogram, corr. length = 0.1'});
g05zr example results
Size of embedding matrix = 64
Approximation not required
Square roots of eigenvalues of embedding matrix:
0.8966 0.8234 0.6810 0.5757 0.5391 0.5757 0.6810 0.8234
0.8940 0.8217 0.6804 0.5756 0.5391 0.5756 0.6804 0.8217
0.8877 0.8175 0.6792 0.5754 0.5391 0.5754 0.6792 0.8175
0.8813 0.8133 0.6780 0.5751 0.5390 0.5751 0.6780 0.8133
0.8787 0.8116 0.6774 0.5750 0.5390 0.5750 0.6774 0.8116
0.8813 0.8133 0.6780 0.5751 0.5390 0.5751 0.6780 0.8133
0.8877 0.8175 0.6792 0.5754 0.5391 0.5754 0.6792 0.8175
0.8940 0.8217 0.6804 0.5756 0.5391 0.5756 0.6804 0.8217
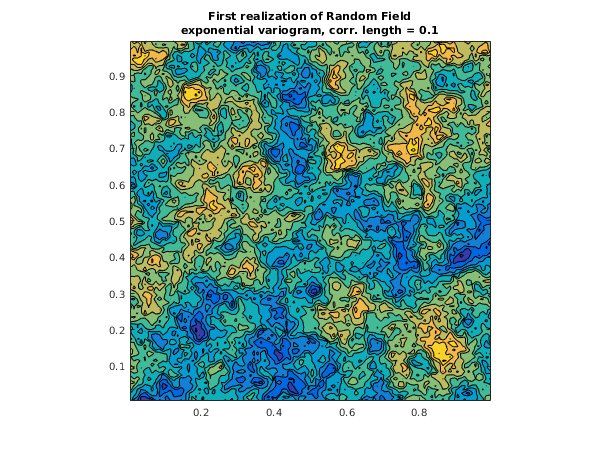
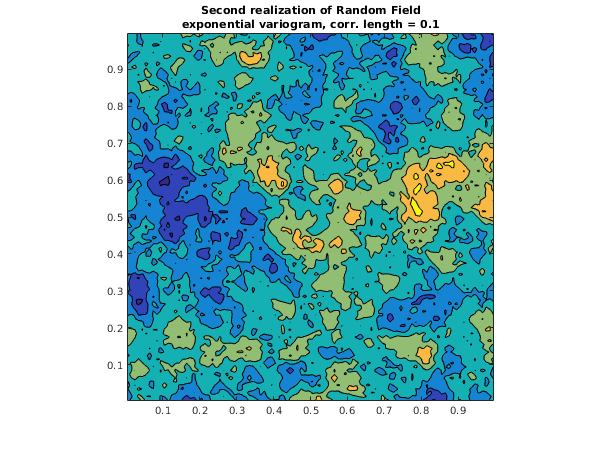
The two plots shown below illustrate the random fields that can be generated by
nag_rand_field_2d_generate (g05zs) using the eigenvalues calculated by
nag_rand_field_2d_predef_setup (g05zr). These are for two realizations of a two-dimensional random field, based on eigenvalues of the embedding matrix for points on a
by
grid. The random field is characterized by the
exponential variogram (
) with correlation lengths both equal to
.
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015

