g01db:: Simple Calculations on Statistical Data (NAG Toolbox)

nag_stat_normal_scores_approx (g01db) calculates an approximation to the set of Normal Scores, i.e., the expected values of an ordered set of independent observations from a Normal distribution with mean

0.0

and standard deviation

1.0

Syntax

Description

nag_stat_normal_scores_approx (g01db) is an adaptation of the Applied Statistics Algorithm AS

177.3

, see Royston (1982). If you are particularly concerned with the accuracy with which nag_stat_normal_scores_approx (g01db) computes the expected values of the order statistics (see Accuracy), then nag_stat_normal_scores_exact (g01da) which is more accurate should be used instead at a cost of increased storage and computing time.

Let

x_{(1)}, x_{(2)}, \dots, x_{(n)}

be the order statistics from a random sample of size

n

from the standard Normal distribution. Defining

P_{r, n} = Φ (- E (x_{(r)}))

and

Q_{r, n} = \frac{r - ε}{n + γ}, r = 1, 2, \dots, n,

where

E (x_{(r)})

is the expected value of

x_{(r)}

, the current function approximates the Normal upper tail area corresponding to

E (x_{(r)})

as,

{\tilde{P}}_{r, n} = Q_{r, n} + \frac{δ_{1}}{n} Q_{r, n}^{λ} + \frac{δ_{2}}{n} Q_{r, n}^{2 λ} - C_{r, n} .

for

r = 1, 2, 3

, and

r \geq 4

. Estimates of

ε

γ

δ_{1}

δ_{2}

and

λ

are obtained. A small correction

C_{r, n}

{\tilde{P}}_{r, n}

is necessary when

r \leq 7

and

n \leq 20

References

Parameters

Compulsory Input Parameters

Optional Input Parameters

Output Parameters

Error Indicators and Warnings

Accuracy

For

n \leq 2000

, the maximum error is

0.0001

, but nag_stat_normal_scores_approx (g01db) is usually accurate to

5

6

decimal places. For

n

up to

5000

, comparison with the exact scores calculated by nag_stat_normal_scores_exact (g01da) shows that the maximum error is

0.001

Further Comments

Example

function g01db_example


fprintf('g01db example results\n\n');

n = int64(10);
[pp, ifail] = g01db(n);

fprintf('Sample size = %5d\n', n);
fprintf('Normal scores\n');
fprintf('              %10.4f%10.4f%10.4f%10.4f%10.4f\n',pp(1:n));

g01db_plot;



function g01db_plot
  % This produces a Q-Q plot for a randomly generated set of data.
  % The normal scores have been calculated using g01db and the sample
  % quantiles obtained by sorting the observed data using m01ca.

  % Initialize the Mersenne Twister generator
  seed = [int64(6324213)];
  genid = int64(3);
  subid = int64(0);

  [state, ifail] = g05kf( ...
                          genid, subid, seed);

  % Generate 50 variates from a Student t distribution with 5 df
  n  = int64(50);
  df = int64(5);
  [state, x, ifail] = g05sn( ...
                             n, df, state);
  % Sort x
  m1 = int64(1);
  [x, ifail] = m01ca(x, m1, 'Ascending');

  % Calculate normal scores
  [pp, ifail] = g01db(n);

  fig1 = figure;
  hold on
  plot(pp,x,'+r',[-2.25 2.25],[-2.25 2.25],'black');
  axis([-2.5 2.5 -3 3]);
  xlabel('Normal scores');
  ylabel('sample Quantiles');
  title({'Q-Q plot for a random set of data','using exact normal scores'});
  hold off;

g01db example results

Sample size =    10
Normal scores
                 -1.5388   -1.0014   -0.6561   -0.3757   -0.1227
                  0.1227    0.3757    0.6561    1.0014    1.5388

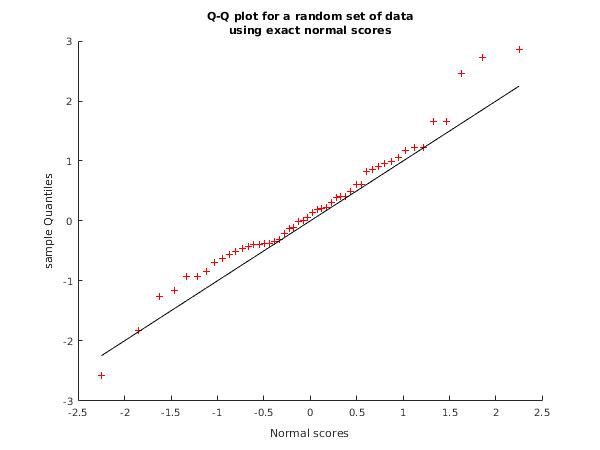
This shows a Q-Q plot for a randomly generated set of data. The normal scores have been calculated using nag_stat_normal_scores_approx (g01db) and the sample quantiles obtained by sorting the observed data using nag_sort_realvec_sort (m01ca). A reference line at

y = x

is also shown.

NAG Toolbox: nag_stat_normal_scores_approx (g01db)

▸▿ Contents

Purpose