PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_sparse_sym_rcm (f11ye)
Purpose
nag_sparse_sym_rcm (f11ye) reduces the bandwidth of a sparse symmetric matrix stored in compressed column storage format using the Reverse Cuthill–McKee algorithm.
Syntax
Description
nag_sparse_sym_rcm (f11ye) takes the compressed column storage (CCS) representation (see
Compressed column storage (CCS) format in the F11 Chapter Introduction) of an
by
symmetric matrix
and applies the Reverse Cuthill–McKee (RCM) algorithm which aims to minimize the bandwidth of the matrix
by reordering the rows and columns symmetrically. This also results in a lower profile of the matrix (see
Further Comments).
nag_sparse_sym_rcm (f11ye) can be useful for solving systems of equations
, as the permuted system
(where
is the permutation matrix described by the vector
perm returned by
nag_sparse_sym_rcm (f11ye)) may require less storage space and/or less computational steps when solving (see
Wai-Hung and Sherman (1976)).
nag_sparse_sym_rcm (f11ye) may be used prior to
nag_sparse_real_symm_precon_ichol (f11ja) and
nag_sparse_real_symm_precon_ichol_solve (f11jb) (see
Example in
nag_sparse_real_symm_precon_ichol_solve (f11jb)).
References
Pissanetsky S (1984) Sparse Matrix Technology Academic Press
Wai-Hung L and Sherman A H (1976) Comparative analysis of the Cuthill–McKee and the reverse Cuthill–McKee ordering algorithms for sparse matrices SIAM J. Numer. Anal. 13(2) 198–213
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int array
-
icolzp records the index into
irowix which starts each new column.
Constraints:
- , for ;
- ;
- , where holds the position integer for the starts of the columns in irowix.
- 2:
– int64int32nag_int array
-
The row indices corresponding to the nonzero elements in the matrix .
Constraint:
, for .
- 3:
– logical array
-
The options to be used by
nag_sparse_sym_rcm (f11ye).
- Row/column of the matrix will only be referenced if , otherwise will be ignored.
- The final permutation will not be reversed, that is, the Cuthill–McKee ordering will be returned. The bandwidth of the non-reversed matrix will be the same but the profile will be the same or larger (see Wai-Hung and Sherman (1976)).
- The matrix will be checked for symmetrical sparsity pattern, otherwise not.
- The bandwidth and profile of the unpermuted matrix will be calculated, otherwise not.
- The bandwidth and profile of the permuted matrix will be calculated, otherwise not.
- 4:
– int64int32nag_int array
-
The dimension of the array
mask
must be at least
if
, and at least
otherwise
mask is only referenced if
is
true. A value of
indicates that the node corresponding to row or column
is not to be referenced. A value of
indicates that the node corresponding to row or column
is to be referenced. In particular, rows and columns not referenced will not be permuted.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
Default:
, the order of the matrix .
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
irowix.
The number of nonzero elements in the matrix .
Constraint:
.
Output Parameters
- 1:
– int64int32nag_int array
-
This will contain the permutation vector that describes the permutation matrix for the reordering of the matrix . The elements of the permutation matrix are zero except for the unit elements in row and column , .
- 2:
– int64int32nag_int array
-
Statistics about the matrix
and the permuted matrix. The quantities below are calculated using any masking in effect otherwise the value zero is returned.
- The bandwidth of the matrix , if .
- The profile of the matrix , if .
- The bandwidth of the permuted matrix , if .
- The profile of the permuted matrix , if .
- 3:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
Constraint: .
-
-
Constraint: .
-
-
Constraint: for all .
-
-
Constraint: for all .
-
-
Constraint: .
Constraint: .
-
-
On entry, the matrix is not symmetric.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
Not applicable.
Further Comments
The bandwidth for a matrix
is defined as
The profile is defined as
Example
This example reads the CCS representation of a real sparse matrix and calls nag_sparse_sym_rcm (f11ye) to reorder the rows and columns and displays the results.
Open in the MATLAB editor:
f11ye_example
function f11ye_example
fprintf('f11ye example results\n\n');
A = bucky;
[irow,icol,a] = find(A);
n = int64(size(A,1));
nz = int64(size(irow,1));
irow = int64(irow);
icol = int64(icol);
dup = 'S';
zero = 'K';
[nz, a, icol, irow, icolzp, ifail] = ...
f11za(...
n, nz, a, icol, irow, dup, zero);
use_mask = false;
do_cm = false;
check_sym = true;
bw_before = true;
bw_after = true;
lopts(1:5) = [use_mask,do_cm,check_sym,bw_before,bw_after];
mask = [int64(0)];
[perm, info, ifail] = f11ye( ...
icolzp, irow, lopts, mask);
disp('Permutation (perm):');
fprintf(' %4d %4d %4d %4d %4d %4d %4d %4d %4d %4d\n',perm)
fprintf('\nStatistics:\n');
fprintf(' Before: Bandwidth = %6d\n', info(1));
fprintf(' Before: Profile = %6d\n', info(2));
fprintf(' After : Bandwidth = %6d\n', info(3));
fprintf(' After : Profile = %6d\n', info(4));
B = A(perm,perm);
fig1 = figure;
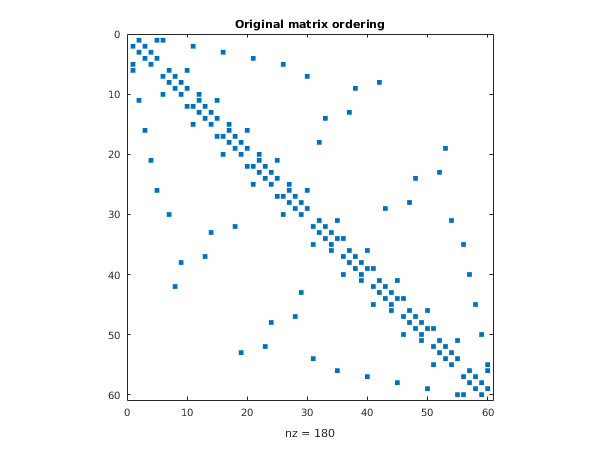
spy(A);
title('Original matrix ordering');
fig2 = figure;
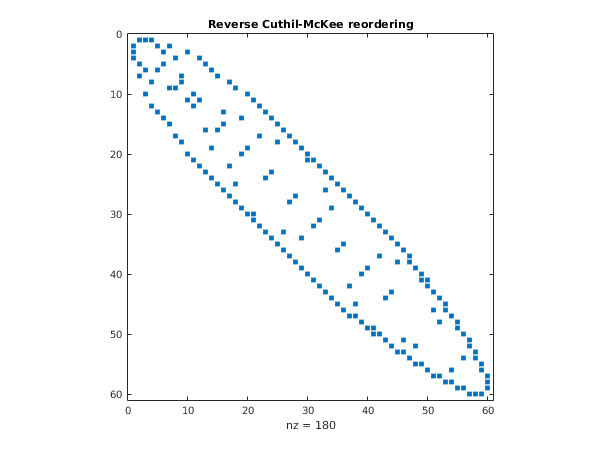
spy(B);
title('Reverse Cuthil-McKee reordering');
f11ye example results
Permutation (perm):
1 5 2 6 4 3 26 7 30 11
12 10 21 16 27 25 8 29 17 15
13 9 22 20 28 24 42 43 18 14
37 38 23 19 47 48 41 44 32 33
36 39 52 53 46 49 45 31 34 40
51 54 50 58 35 57 55 59 56 60
Statistics:
Before: Bandwidth = 34
Before: Profile = 490
After : Bandwidth = 10
After : Profile = 458
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015