PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_matop_real_gen_blkdiag_lu (f01lh)
Purpose
nag_matop_real_gen_blkdiag_lu (f01lh) factorizes a real almost block diagonal matrix.
Syntax
[
a,
pivot,
tol,
kpivot,
ifail] = f01lh(
n,
blkstr,
a,
tol, 'nbloks',
nbloks, 'lena',
lena)
[
a,
pivot,
tol,
kpivot,
ifail] = nag_matop_real_gen_blkdiag_lu(
n,
blkstr,
a,
tol, 'nbloks',
nbloks, 'lena',
lena)
Description
nag_matop_real_gen_blkdiag_lu (f01lh) factorizes a real almost block diagonal matrix,
, by row elimination with alternate row and column pivoting such that no ‘fill-in’ is produced. The code, which is derived from ARCECO described in
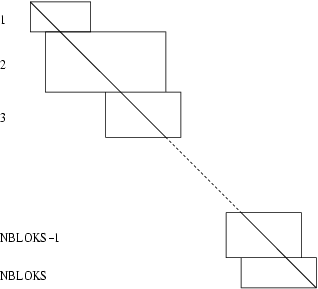
Diaz et al. (1983), uses Level 1 and Level 2 BLAS. No three successive diagonal blocks may have columns in common and therefore the almost block diagonal matrix must have the form shown in the following diagram:
Figure 1
This function may be followed by
nag_linsys_real_blkdiag_fac_solve (f04lh), which is designed to solve sets of linear equations
or
.
References
Diaz J C, Fairweather G and Keast P (1983) Fortran packages for solving certain almost block diagonal linear systems by modified alternate row and column elimination ACM Trans. Math. Software 9 358–375
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
, the order of the matrix .
Constraint:
.
- 2:
– int64int32nag_int array
-
Information which describes the block structure of
as follows:
- must contain the number of rows in the th block, ;
- must contain the number of columns in the th block, ;
- must contain the number of columns of overlap between the th and th blocks, . need not be set.
The following conditions delimit the structure of
:
- ,
- ,
(there must be at least one column and one row in each block and a non-negative number of columns of overlap);
- ,
(the total number of columns in overlaps in each block must not exceed the number of columns in that block);
- ,
- , ,
- ,
(the index of the first column of the overlap between the
th and
th blocks must be
the index of the last row of the
th block, and the index of the last column of overlap must be
the index of the last row of the
th block);
- ,
- ,
(both the number of rows and the number of columns of
must equal
).
- 3:
– double array
-
The elements of the almost block diagonal matrix stored block by block, with each block stored column by column. The sizes of the blocks and the overlaps are defined by the argument
blkstr.
If
is the first element in the
th block, then an arbitrary element
in the
th block must be stored in the array element:
where
is the base address of the
th block, and
is the number of rows of the
th block.
See
Further Comments for comments on scaling.
- 4:
– double scalar
-
A relative tolerance to be used to indicate whether or not the matrix is singular. For a discussion on how
tol is used see
Further Comments. If
tol is non-positive, then
tol is reset to
, where
is the
machine precision.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the array
blkstr.
, the total number of blocks of the matrix .
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Default:
the dimension of the array
a.
The dimension of the array
a.
Constraint:
.
Output Parameters
- 1:
– double array
-
The factorized form of the matrix.
- 2:
– int64int32nag_int array
-
Details of the interchanges.
- 3:
– double scalar
-
Unchanged unless on entry, in which case it is set to .
- 4:
– int64int32nag_int scalar
-
If
,
kpivot contains the value
, where
is the first position on the diagonal of the matrix
where too small a pivot was detected. Otherwise
kpivot is set to
.
- 5:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
| On entry, | , |
| or | , |
| or | , |
| or | lena is too small, |
| or | illegal values detected in blkstr. |
- W
-
The factorization has been completed, but a small pivot has been detected.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy of nag_matop_real_gen_blkdiag_lu (f01lh) depends on the conditioning of the matrix .
Further Comments
Singularity or near singularity in
is determined by the argument
tol. If the absolute value of any pivot is less than
, where
is the maximum absolute value of an element of
, then
is said to be singular. The position on the diagonal of
of the first of any such pivots is indicated by the argument
kpivot. The factorization, and the test for near singularity, will be more accurate if before entry
is scaled so that the
-norms of the rows and columns of
are all of approximately the same order of magnitude. (The
-norm is the maximum absolute value of any element in the row or column.)
Example
This example solves the set of linear equations
where
and
The exact solution is
Open in the MATLAB editor:
f01lh_example
function f01lh_example
fprintf('f01lh example results\n\n');
n = int64(18);
blkstr = [int64(2),4,5,3,4;
4, 7,8,6,5;
3, 4,2,3,0];
a1 = [-1.00 -0.98 -0.79 -0.15;
-1.00 0.25 -0.87 0.35];
a2 = [ 0.78 0.31 -0.85 0.89 -0.69 -0.98 -0.76;
-0.82 0.12 -0.01 0.75 0.32 -1.00 -0.53;
-0.83 -0.98 -0.58 0.04 0.87 0.38 -1.00;
-0.21 -0.93 -0.84 0.37 -0.94 -0.96 -1.00];
a3 = [-0.99 -0.91 -0.28 0.90 0.78 -0.93 -0.76 0.48;
-0.87 -0.14 -1.00 -0.59 -0.99 0.21 -0.73 -0.48;
-0.93 -0.91 0.10 -0.89 -0.68 -0.09 -0.58 -0.21;
0.85 -0.39 0.79 -0.71 0.39 -0.99 -0.12 -0.75;
0.17 -1.37 1.29 -1.59 1.10 -1.63 -1.01 -0.27];
a4 = [ 0.08 0.61 0.54 -0.41 0.16 -0.46;
-0.67 0.56 -0.99 0.16 -0.16 0.98;
-0.24 -0.41 0.40 -0.93 0.70 0.43];
a5 = [ 0.71 -0.97 -0.60 -0.30 0.18;
-0.47 -0.98 -0.73 0.07 0.04;
-0.25 -0.92 -0.52 -0.46 -0.58;
0.89 -0.94 -0.54 -1.00 -0.36];
a = [reshape(a1,[ 8,1]);
reshape(a2,[28,1]);
reshape(a3,[40,1]);
reshape(a4,[18,1]);
reshape(a5,[20,1])];
b = [-2.92; -1.27; -1.30; -1.17; -2.10; -4.51; -1.71; -4.59;
-4.19; -0.93; -3.31; 0.52; -0.12; -0.05; -0.98; -2.07;
-2.73; -1.95];
tol = 0;
[AF, pivot, tol, index, ifail] = ...
f01lh(n, blkstr, a, tol);
trans = 'N';
[x, ifail] = f04lh( ...
trans, blkstr, AF, pivot, b);
disp('Component solution');
disp(x);
f01lh example results
Component solution
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015