1: $a (ia)$ – double array: $a (j + 1)$ , for $j = 1, 2, \dots, l + 1$ , must contain the value of the coefficient $a_{j}$ in the numerator of the rational function.
2: $b (ib)$ – double array: $b (k + 1)$ , for $k = 1, 2, \dots, m + 1$ , must contain the value of the coefficient $b_{k}$ in the denominator of the rational function.

Constraint: if $ib = 1$ , $b (1) \neq 0.0$ .
3: $x$ – double scalar: The point $x$ at which the rational function is to be evaluated.

Optional Input Parameters

1: $ia$ – int64int32nag_int scalar: Default: the dimension of the array a.
The value of $l + 1$ , where $l$ is the degree of the numerator.

Constraint: $ia \geq 1$ .
2: $ib$ – int64int32nag_int scalar: Default: the dimension of the array b.
The value of $m + 1$ , where $m$ is the degree of the denominator.

Constraint: $ib \geq 1$ .

Output Parameters

1: $ans$ – double scalar: The result of evaluating the rational function at the given point $x$ .
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$: The rational function is being evaluated at or near a pole.

$ifail = 2$

On entry,	$ia < 1$ ,
or	$ib < 1$ ,
or	$b (1) = 0.0$ when $ib = 1$ (so the denominator is identically zero).

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

A running error analysis for polynomial evaluation by nested multiplication using the recurrence suggested by Kahan (see Peters and Wilkinson (1971)) is used to detect whether you are attempting to evaluate the approximant at or near a pole.

Further Comments

The time taken is approximately proportional to

l + m

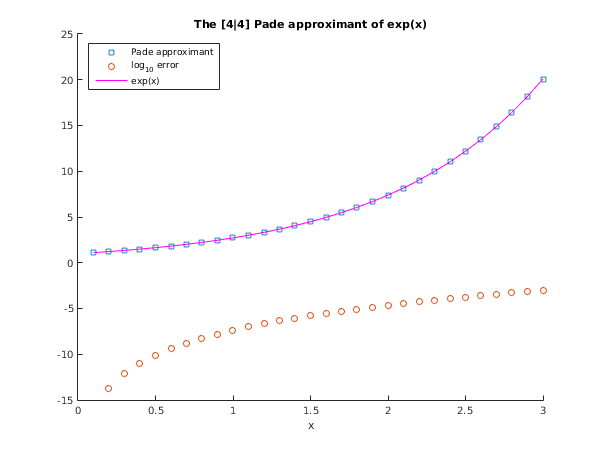
Example

This example first calls nag_fit_pade_app (e02ra) to calculate the

4 / 4

Padé approximant to

e^{x}

, and then uses nag_fit_pade_eval (e02rb) to evaluate the approximant at

x = 0.1, 0.2, \dots, 1.0

Open in the MATLAB editor: e02rb_example

function e02rb_example


fprintf('e02rb example results\n\n');

ia = int64(5);
ib = int64(5);
ic = ia + ib - 1;
c  = ones(ic,1);
for j = 3:ic
  c(j) = c(j-1)/double(j-1);
end

[a, b, ifail] = e02ra(ia, ib, c);

fprintf('    x        Pade       exp(x)      error\n');
for j=1:30
  x = j/10;
  [padx, ifail] = e02rb(a, b, x);
  f(j) = padx;
  expx = exp(x);
  relerr = abs(expx-padx)/expx;
  err(j) = relerr;
  if (mod(j,3)==1)
    fprintf('%6.1f%12.5f%12.5f%13.2e\n', x, padx, expx, relerr);
  end
end

x = [0.1:0.1:3];
fig1 = figure;
hold on;
plot(x,f,'s',x,log10(err),'o');
plot(x,exp(x),'Color','Magenta');
legend('Pade approximant','log_{10} error','exp(x)','Location','NorthWest');
title('The [4|4] Pade approximant of exp(x)');
xlabel('x');
hold off;

e02rb example results

    x        Pade       exp(x)      error
   0.1     1.10517     1.10517     0.00e+00
   0.4     1.49182     1.49182     1.04e-11
   0.7     2.01375     2.01375     1.61e-09
   1.0     2.71828     2.71828     4.05e-08
   1.3     3.66930     3.66930     4.39e-07
   1.6     4.95302     4.95303     2.91e-06
   1.9     6.68580     6.68589     1.41e-05
   2.2     9.02452     9.02501     5.47e-05
   2.5    12.18030    12.18249     1.80e-04
   2.8    16.43608    16.44465     5.21e-04

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox