NAG Toolbox: nag_interp_1d_monotonic_deriv (e01bg)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{x}\left(\mathbf{n}\right)$ – double array

2:     $\mathrm{f}\left(\mathbf{n}\right)$ – double array

3:     $\mathrm{d}\left(\mathbf{n}\right)$ – double array

n, x, f and d must be unchanged from the previous call of nag_interp_1d_monotonic (e01be).

4:     $\mathrm{px}\left(\mathbf{m}\right)$ – double array

The $m$ values of $x$ at which the interpolant is to be evaluated.

Optional Input Parameters

1:     $\mathrm{n}$ – int64int32nag_int scalar

Default: the dimension of the arrays x, f, d. (An error is raised if these dimensions are not equal.)

n, x, f and d must be unchanged from the previous call of nag_interp_1d_monotonic (e01be).

2:     $\mathrm{m}$ – int64int32nag_int scalar

Default: the dimension of the array px.

$m$, the number of points at which the interpolant is to be evaluated.

Constraint: $\mathbf{m}\ge 1$.

Output Parameters

1:     $\mathrm{pf}\left(\mathbf{m}\right)$ – double array

$\mathbf{pf}\left(\mathit{i}\right)$ contains the value of the interpolant evaluated at the point $\mathbf{px}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,m$.

2:     $\mathrm{pd}\left(\mathbf{m}\right)$ – double array

$\mathbf{pd}\left(\mathit{i}\right)$ contains the first derivative of the interpolant evaluated at the point $\mathbf{px}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,m$.

3:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   $\mathbf{ifail}=1$

On entry,

$\mathbf{n}<2$.

   $\mathbf{ifail}=2$

The values of $\mathbf{x}\left(\mathit{r}\right)$, for $\mathit{r}=1,2,\dots ,\mathbf{n}$, are not in strictly increasing order.

   $\mathbf{ifail}=3$

On entry,

$\mathbf{m}<1$.

W  $\mathbf{ifail}=4$

At least one of the points $\mathbf{px}\left(\mathit{i}\right)$, for $\mathit{i}=1,2,\dots ,\mathbf{m}$, lies outside the interval [$\mathbf{x}\left(1\right),\mathbf{x}\left(\mathbf{n}\right)$], and extrapolation was performed at all such points. Values computed at these points may be very unreliable.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: e01bg_example

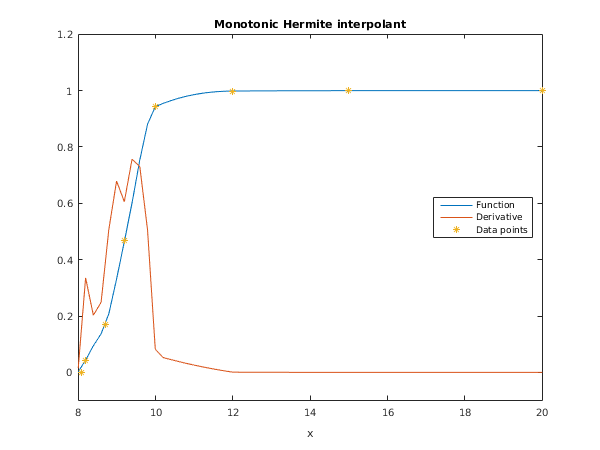
function e01bg_example


fprintf('e01bg example results\n\n');

x = [7.99 8.09    8.19    8.7     9.2     10      12      15      20];
f = [0 2.7643e-05 0.04375 0.16918 0.46943 0.94374 0.99864 0.99992 0.99999];

% Theses are as returned by e01be(x,f)
d = [0;
     0.00055251;
     0.33587;
     0.34944;
     0.59696;
     0.060326;
     0.000898335;
     2.93954e-05;
     0];

m = 11;
dx = (x(end)-x(1))/(m-1);
px = [x(1):dx:x(end)];

[pf, pd, ifail] = e01bg(x, f, d, px);

fprintf('\n                Interpolated   Interpolated\n');
fprintf('     Abscissa          Value     Derivative\n');
fprintf('%13.4f%15.4f%15.3e\n', [px' pf pd]');

% Recalculate on finer mesh for plotting
m = 61;
dx = (x(end)-x(1))/(m-1);
px = [x(1):dx:x(end)];

[pf, pd, ifail] = e01bg(x, f, d, px);

fig1 = figure;
plot(px,pf,px,pd,x,f,'*');
legend('Function','Derivative','Data points','Location','East');
title('Monotonic Hermite interpolant');
xlabel('x');
axis([8 20 -0.1 1.2]);

e01bg example results


                Interpolated   Interpolated
     Abscissa          Value     Derivative
       7.9900         0.0000      0.000e+00
       9.1910         0.4640      6.060e-01
      10.3920         0.9645      4.569e-02
      11.5930         0.9965      9.917e-03
      12.7940         0.9992      6.249e-04
      13.9950         0.9998      2.708e-04
      15.1960         0.9999      2.809e-05
      16.3970         1.0000      2.034e-05
      17.5980         1.0000      1.308e-05
      18.7990         1.0000      6.297e-06
      20.0000         1.0000     -3.388e-21