nag_mesh_2d_renumber (d06cc) uses a Gibbs method to renumber the vertices of a given mesh in order to reduce the bandwidth of the associated finite element matrix
. This matrix has elements
such that:
This function reduces the bandwidth
, which is the smallest integer such that
whenever
(see
Gibbs et al. (1976) for details about that method).
nag_mesh_2d_renumber (d06cc) also returns the sparsity structure of the matrix associated with the renumbered mesh.
This function is derived from material in the MODULEF package from INRIA (Institut National de Recherche en Informatique et Automatique).
Gibbs N E, Poole W G Jr and Stockmeyer P K (1976) An algorithm for reducing the bandwidth and profile of a sparse matrix SIAM J. Numer. Anal. 13 236–250
- 1:
– int64int32nag_int scalar
-
The maximum number of nonzero entries in the matrix based on the input mesh. It is the dimension of the arrays
irow and
icol as declared in the function from which
nag_mesh_2d_renumber (d06cc) is called.
Constraint:
.
- 2:
– double array
-
contains the coordinate of the th input mesh vertex, for ; while contains the corresponding coordinate.
- 3:
– int64int32nag_int array
-
The specification of the boundary or interface edges. and contain the vertex numbers of the two end points of the th boundary edge. is a user-supplied tag for the th boundary or interface edge: for an interior edge and has a nonzero tag otherwise.
Constraint:
and , for and .
- 4:
– int64int32nag_int array
-
The connectivity of the mesh between triangles and vertices. For each triangle
, gives the indices of its three vertices (in anticlockwise order), for and .
Constraint:
and and and , for and .
- 5:
– int64int32nag_int scalar
-
The level of trace information required from
nag_mesh_2d_renumber (d06cc).
- No output is generated.
- Information about the effect of the renumbering on the finite element matrix are output. This information includes the half bandwidth and the sparsity structure of this matrix before and after renumbering.
- The output is similar to that produced when but the sparsities (for each row of the matrix, indices of nonzero entries) of the matrix before and after renumbering are also output.
Not applicable.
None.
In this example, a geometry with two holes (two interior circles inside an exterior one) is considered. The geometry has been meshed using the simple incremental method (
nag_mesh_2d_gen_inc (d06aa)) and it has
vertices and
triangles. The function
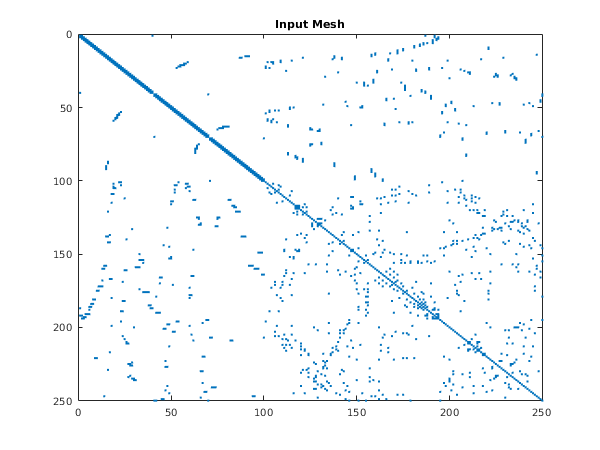
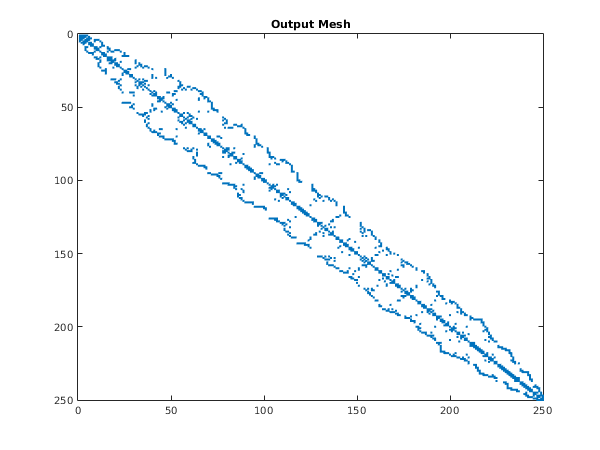
nag_mesh_2d_gen_boundary (d06ba) is used to renumber the vertices, and one can see the benefit in terms of the sparsity of the finite element matrix based on the renumbered mesh.
function d06cc_example
fprintf('d06cc example results\n\n');
edge = zeros(3, 100, 'int64');
coor = zeros(2, 250);
ncirc = 3;
nvertices = [40, 30, 30];
radii = [1, 0.49, 0.15];
centres = [0, 0; -0.5, 0; -0.5, 0.65];
csign = 1;
i1 = 0;
nvb = 0;
for icirc = 1:ncirc
for i = 0:nvertices(icirc)-1
i1 = i1+1;
theta = 2*pi*i/nvertices(icirc);
coor(1,i1) = radii(icirc)*cos(theta) + centres(icirc, 1);
coor(2,i1) = csign*radii(icirc)*sin(theta) + centres(icirc, 2);
edge(1,i1) = i1;
edge(2,i1) = i1 + 1;
edge(3,i1) = 1;
end
edge(2,i1) = nvb + 1;
nvb = nvb + nvertices(icirc);
csign = -1;
end
nedge = nvb;
bspace = zeros(1, 100);
bspace(1:nvb) = 0.05;
smooth = true;
itrace = int64(0);
nnzmax = int64(3000);
[nv, nelt, coor, conn, ifail] = d06aa(edge, coor, bspace, smooth, itrace);
[nz, irow, icol, ifail] = d06cb(nv, nnzmax, conn, 'nelt', nelt);
fprintf('\nNumber of non-zero entries in input mesh: %d\n', nz);
fig1 = figure;
plot(irow(1:double(nz)), icol(1:double(nz)), '.');
title ('Input Mesh');
set(gca,'YDir','reverse');
[nz, coor, edge, conn, irow, icol, ifail] = ...
d06cc(nnzmax, coor, edge, conn, itrace, 'nelt', nelt);
fprintf('Number of non-zero entries in output mesh: %d\n', nz);
fig2 = figure;
plot(irow(1:double(nz)), icol(1:double(nz)), '.');
title ('Output Mesh');
set(gca,'YDir','reverse');