NAG Toolbox: nag_mesh_2d_smooth_bary (d06ca)

Purpose

Syntax

Description

References

Parameters

Compulsory Input Parameters

1:     $\mathrm{coor}\left(2,\mathbf{nv}\right)$ – double array

$\mathbf{coor}\left(1,\mathit{i}\right)$ contains the $x$ coordinate of the $\mathit{i}$th input mesh vertex, for $\mathit{i}=1,2,\dots ,\mathbf{nv}$; while $\mathbf{coor}\left(2,\mathit{i}\right)$ contains the corresponding $y$ coordinate.

2:     $\mathrm{edge}\left(3,\mathbf{nedge}\right)$ – int64int32nag_int array

The specification of the boundary or interface edges. $\mathbf{edge}\left(1,j\right)$ and $\mathbf{edge}\left(2,j\right)$ contain the vertex numbers of the two end points of the $j$th boundary edge. $\mathbf{edge}\left(3,j\right)$ is a user-supplied tag for the $j$th boundary or interface edge: $\mathbf{edge}\left(3,j\right)=0$ for an interior edge and has a nonzero tag otherwise.

Constraint: $1\le \mathbf{edge}\left(\mathit{i},\mathit{j}\right)\le \mathbf{nv}$ and $\mathbf{edge}\left(1,\mathit{j}\right)\ne \mathbf{edge}\left(2,\mathit{j}\right)$, for $\mathit{i}=1,2$ and $\mathit{j}=1,2,\dots ,\mathbf{nedge}$.

3:     $\mathrm{conn}\left(3,\mathbf{nelt}\right)$ – int64int32nag_int array

The connectivity of the mesh between triangles and vertices. For each triangle $\mathit{j}$, $\mathbf{conn}\left(\mathit{i},\mathit{j}\right)$ gives the indices of its three vertices (in anticlockwise order), for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt}$.

Constraint: $1\le \mathbf{conn}\left(\mathit{i},\mathit{j}\right)\le \mathbf{nv}$ and $\mathbf{conn}\left(1,\mathit{j}\right)\ne \mathbf{conn}\left(2,\mathit{j}\right)$ and $\mathbf{conn}\left(1,\mathit{j}\right)\ne \mathbf{conn}\left(3,\mathit{j}\right)$ and $\mathbf{conn}\left(2,\mathit{j}\right)\ne \mathbf{conn}\left(3,\mathit{j}\right)$, for $\mathit{i}=1,2,3$ and $\mathit{j}=1,2,\dots ,\mathbf{nelt}$.

4:     $\mathrm{numfix}\left(:\right)$ – int64int32nag_int array

The dimension of the array numfix must be at least $\max \left(1,\mathbf{nvfix}\right)$

The indices in coor of fixed interior vertices of the input mesh.

Constraint: if $\mathbf{nvfix}>0$, $1\le \mathbf{numfix}\left(\mathit{i}\right)\le \mathbf{nv}$, for $\mathit{i}=1,2,\dots ,\mathbf{nvfix}$.

5:     $\mathrm{itrace}$ – int64int32nag_int scalar

The level of trace information required from nag_mesh_2d_smooth_bary (d06ca).

$\mathbf{itrace}\le 0$

No output is generated.

$\mathbf{itrace}=1$

A histogram of the triangular element qualities is printed on the current advisory message unit (see nag_file_set_unit_advisory (x04ab)) before and after smoothing. This histogram gives the lowest and the highest triangle quality as well as the number of elements lying in each of the nqint equal intervals between the extremes.

$\mathbf{itrace}>1$

The output is similar to that produced when $\mathbf{itrace}=1$ but the connectivity between vertices and triangles (for each vertex, the list of triangles in which it appears) is given.

You are advised to set $\mathbf{itrace}=0$, unless you are experienced with finite element meshes.

6:     $\mathrm{nqint}$ – int64int32nag_int scalar

The number of intervals between the extreme quality values for the input and the smoothed mesh.

If $\mathbf{itrace}=0$, nqint is not referenced.

Optional Input Parameters

1:     $\mathrm{nv}$ – int64int32nag_int scalar

Default: the dimension of the array coor.

The total number of vertices in the input mesh.

Constraint: $\mathbf{nv}\ge 3$.

2:     $\mathrm{nelt}$ – int64int32nag_int scalar

Default: the dimension of the array conn.

The number of triangles in the input mesh.

Constraint: $\mathbf{nelt}\le 2\times \mathbf{nv}-1$.

3:     $\mathrm{nedge}$ – int64int32nag_int scalar

Default: the dimension of the array edge.

The number of the boundary and interface edges in the input mesh.

Constraint: $\mathbf{nedge}\ge 1$.

4:     $\mathrm{nvfix}$ – int64int32nag_int scalar

Default: the dimension of the array numfix.

The number of fixed vertices in the input mesh.

Constraint: $0\le \mathbf{nvfix}\le \mathbf{nv}$.

Output Parameters

1:     $\mathrm{coor}\left(2,\mathbf{nv}\right)$ – double array

$\mathbf{coor}\left(1,\mathit{i}\right)$ will contain the $x$ coordinate of the $\mathit{i}$th smoothed mesh vertex, for $\mathit{i}=1,2,\dots ,\mathbf{nv}$; while $\mathbf{coor}\left(2,\mathit{i}\right)$ will contain the corresponding $y$ coordinate. Note that the coordinates of boundary and interface edge vertices, as well as those specified by you (see the description of numfix), are unchanged by the process.

2:     $\mathrm{ifail}$ – int64int32nag_int scalar

$\mathbf{ifail}=\mathbf{0}$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

   $\mathbf{ifail}=1$

On entry,	$\mathbf{nv}<3$,
or	$\mathbf{nelt}>2\times \mathbf{nv}-1$,
or	$\mathbf{nedge}<1$,
or	$\mathbf{edge}\left(i,j\right)<1$ or $\mathbf{edge}\left(i,j\right)>\mathbf{nv}$ for some $i=1,2$ and $j=1,2,\dots ,\mathbf{nedge}$,
or	$\mathbf{edge}\left(1,j\right)=\mathbf{edge}\left(2,j\right)$ for some $j=1,2,\dots ,\mathbf{nedge}$,
or	$\mathbf{conn}\left(i,j\right)<1$ or $\mathbf{conn}\left(i,j\right)>\mathbf{nv}$ for some $i=1,2,3$ and $j=1,2,\dots ,\mathbf{nelt}$,
or	$\mathbf{conn}\left(1,j\right)=\mathbf{conn}\left(2,j\right)$ or $\mathbf{conn}\left(1,j\right)=\mathbf{conn}\left(3,j\right)$ or $\mathbf{conn}\left(2,j\right)=\mathbf{conn}\left(3,j\right)$ for some $j=1,2,\dots ,\mathbf{nelt}$,
or	$\mathbf{nvfix}<0$ or $\mathbf{nvfix}>\mathbf{nv}$,
or	$\mathbf{numfix}\left(i\right)<1$ or $\mathbf{numfix}\left(i\right)>\mathbf{nv}$ for some $i=1,2,\dots ,\mathbf{nvfix}$ if $\mathbf{nvfix}>0$,
or	$\mathit{liwork}<8\times \mathbf{nelt}+2\times \mathbf{nv}$,
or	$\mathit{lrwork}<2\times \mathbf{nv}+\mathbf{nelt}$.

   $\mathbf{ifail}=2$

A serious error has occurred in an internal call to an auxiliary function. Check the input mesh, especially the connectivity between triangles and vertices (the argument conn). Setting $\mathbf{itrace}>1$ may provide more information. If the problem persists, contact NAG.

   $\mathbf{ifail}=-99$

An unexpected error has been triggered by this routine. Please contact NAG.

   $\mathbf{ifail}=-399$

Your licence key may have expired or may not have been installed correctly.

   $\mathbf{ifail}=-999$

Dynamic memory allocation failed.

Accuracy

Further Comments

Example

Open in the MATLAB editor: d06ca_example

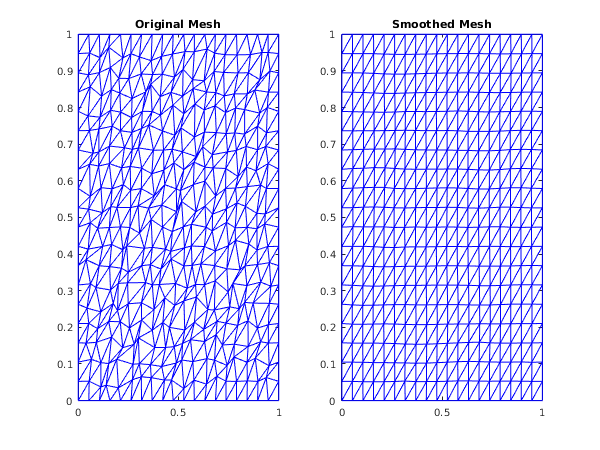
function d06ca_example


fprintf('d06ca example results\n\n');

imax = 20;
jmax = 20;
delta = 87;
nv = imax*jmax;

hx = 1/(imax-1);
hy = 1/(jmax-1);
rad = 0.01*delta*min(hx,hy)/2;

% Initialise the seed for the random number generator
seed = [int64(1762541)];
% genid and subid identify the base generator
genid = int64(1);
subid = int64(1);
% Initialise the generator to a repeatable sequence
[state, ifail] = g05kf(genid, subid, seed);

% Generate two sets of uniform random variates
[state, x1, ifail] = g05sq(int64(nv), 0, rad, state);
[state, x2, ifail] = g05sq(int64(nv), 0, 2*pi, state);

% Generate a simple uniform mesh and then distort it
% randomly within the distortion neighbourhood of each node.
coor = zeros(2, nv);
conn = zeros(3, 2*nv-1, 'int64');
k = 0;
ind = 0;
for j = 1:jmax
  for i = 1:imax
    k = k + 1;
    r = x1(k);
    theta = x2(k);

    if (i==1 || i==imax || j==1 || j==jmax)
      r = 0;
    end

    coor(1,k) = (i-1)*hx + r*cos(theta);
    coor(2,k) = (j-1)*hy + r*sin(theta);

    if (i<imax && j<jmax)
      ind = ind + 1;
      conn(1,ind) = k;
      conn(2,ind) = k + 1;
      conn(3,ind) = k + imax + 1;
      ind = ind + 1;
      conn(1,ind) = k;
      conn(2,ind) = k + imax + 1;
      conn(3,ind) = k + imax;
    end
  end
end

nelt = ind;

% Boundary edges
nedge = 0;
edge = zeros(3, 100, 'int64');
for i = 1:imax - 1
  nedge = nedge + 1;
  edge(1,nedge) = i;
  edge(2,nedge) = i + 1;
  edge(3,nedge) = 0;
end

for i = 1:jmax - 1
  nedge = nedge + 1;
  edge(1,nedge) = i*imax;
  edge(2,nedge) = (i+1)*imax;
  edge(3,nedge) = 0;
end

for i = 1:imax - 1
  nedge = nedge + 1;
  edge(1,nedge) = imax*jmax - i + 1;
  edge(2,nedge) = imax*jmax - i;
  edge(3,nedge) = 0;
end

for i = 1:jmax - 1
  nedge = nedge + 1;
  edge(1,nedge) = (jmax-i)*imax + 1;
  edge(2,nedge) = (jmax-i-1)*imax + 1;
  edge(3,nedge) = 0;
end

numfix = zeros(0, 0, 'int64');
itrace = int64(1);
nqint = int64(10);

% Plot original mesh
fig1 = figure;
subplot(1,2,1);
triplot(transpose(double(conn(:,1:nelt))), coor(1,:), coor(2,:));
title ('Original Mesh');

[coor, ifail] = d06ca(coor, edge(:, 1:nedge), conn(:, 1:nelt), ...
                      numfix, itrace, nqint);

fprintf('\nComplete smooth mesh characteristics:\n');
fprintf('  nv    = %d\n', nv);
fprintf('  nelt  = %d\n', nelt);

% Plot smoothed mesh
subplot(1,2,2);
triplot(transpose(double(conn(:,1:nelt))), coor(1,:), coor(2,:));
title ('Smoothed Mesh');

d06ca example results

 BEFORE SMOOTHING
 Minimum smoothness measure:       1.0060557
 Maximum smoothness measure:      45.7310387
 Distribution interval            Number of elements
      1.0060557 -       5.4785540       715
      5.4785540 -       9.9510523         4
      9.9510523 -      14.4235506         1
     14.4235506 -      18.8960489         0
     18.8960489 -      23.3685472         0
     23.3685472 -      27.8410455         0
     27.8410455 -      32.3135438         0
     32.3135438 -      36.7860421         0
     36.7860421 -      41.2585404         0
     41.2585404 -      45.7310387         1

 AFTER SMOOTHING
 Minimum smoothness measure:       1.3377832
 Maximum smoothness measure:       1.4445226
 Distribution interval            Number of elements
      1.3377832 -       1.3484572         0
      1.3484572 -       1.3591311        13
      1.3591311 -       1.3698050        42
      1.3698050 -       1.3804790       104
      1.3804790 -       1.3911529       162
      1.3911529 -       1.4018268       159
      1.4018268 -       1.4125008       122
      1.4125008 -       1.4231747        74
      1.4231747 -       1.4338486        31
      1.4338486 -       1.4445226        14

Complete smooth mesh characteristics:
  nv    = 400
  nelt  = 722