PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_pde_3d_ellip_fd_iter (d03ub)
Purpose
nag_pde_3d_ellip_fd_iter (d03ub) performs at each call one iteration of the Strongly Implicit Procedure. It is used to calculate on successive calls a sequence of approximate corrections to the current estimate of the solution when solving a system of simultaneous algebraic equations for which the iterative update matrix is of seven-point molecule form on a three-dimensional topologically-rectangular mesh. (‘Topological’ means that a polar grid , for example, can be used as it is equivalent to a rectangular box.)
Syntax
[
r,
ifail] = d03ub(
n1,
n2,
n3,
a,
b,
c,
d,
e,
f,
g,
aparam,
it,
r, 'sda',
sda)
[
r,
ifail] = nag_pde_3d_ellip_fd_iter(
n1,
n2,
n3,
a,
b,
c,
d,
e,
f,
g,
aparam,
it,
r, 'sda',
sda)
Description
Given a set of simultaneous equations
(which could be nonlinear) derived, for example, from a finite difference representation of a three-dimensional elliptic partial differential equation and its boundary conditions, the solution
may be obtained iteratively from a starting approximation
by the formulae
Thus
is the residual of the
th approximate solution
, and
is the update change vector.
nag_pde_3d_ellip_fd_iter (d03ub) determines the approximate change vector
corresponding to a given residual
, i.e., it determines an approximate solution to a set of equations
where
is a square
by
matrix and
is a known vector of length
. The set of equations
(2) must be of seven-diagonal form
for
,
and
, provided that
. Indeed, if
, then the equation is assumed to be
The calling program supplies the current residual
at each iteration and the coefficients of the seven-point molecule system of equations on which the update procedure is based. The function performs one iteration, using the approximate
factorization of the Strongly Implicit Procedure with the necessary acceleration argument adjustment, to calculate the approximate solution
of the set of equations
(2). The change
overwrites the residual array for return to the calling program. The calling program must combine this change stored in
with the old approximation to obtain the new approximate solution for
. It must then recalculate the residuals and, if the accuracy requirements have not been satisfied, commence the next iterative cycle.
Clearly there is no requirement that the iterative update matrix passed in the form of the seven-diagonal element arrays
a,
b,
c,
d,
e,
f and
g is the same as that used to calculate the residuals, and therefore the one governing the problem. However, the convergence may be impaired if they are not equal. Indeed, if the system of equations
(1) is not precisely of the seven-diagonal form illustrated above but has a few additional terms, then the methods of deferred or defect correction can be employed. The residual is calculated by the calling program using the full system of equations, but the update formula is based on a seven-diagonal system
(2) of the form given above. For example, the solution of a system of eleven-diagonal equations each involving the combination of terms with
and
could use the seven-diagonal coefficients on which to base the update, provided these incorporate the major features of the equations.
Problems in topologically non-rectangular box-shaped regions can be solved using the function by surrounding the region with a circumscribing topologically rectangular box. The equations for the nodal values external to the region of interest are set to zero (i.e., ) and the boundary conditions are incorporated into the equations for the appropriate nodes.
If there is no better initial approximation when starting the iterative cycle, one can use an array of all zeros as the initial approximation from which the first set of residuals are determined.
The function can be used to solve linear elliptic equations in which case the arrays
a,
b,
c,
d,
e,
f and
g and the quantities
will be unchanged during the iterative cycles, or for solving nonlinear elliptic equations in which case some or all of these arrays may require updating as each new approximate solution is derived. Depending on the nonlinearity, some under-relaxation of the coefficients and/or source terms may be needed during their recalculation using the new estimates of the solution (see
Jacobs (1972)).
The function can also be used to solve each step of a time-dependent parabolic equation in three space dimensions. The solution at each time step can be expressed in terms of an elliptic equation if the Crank–Nicolson or other form of implicit time integration is used.
Neither diagonal dominance, nor positive-definiteness, of the matrix
or of the update matrix formed from the arrays
a,
b,
c,
d,
e,
f and
g is necessary to ensure convergence.
For problems in which the solution is not unique, in the sense that an arbitrary constant can be added to the solution (for example Poisson's equation with all Neumann boundary conditions), the calling program should subtract a typical nodal value from the whole solution at every iteration to keep rounding errors to a minimum for those cases when convergence is slow. For such problems there is generally an associated compatibility condition. For the example mentioned this compatibility condition equates the total net source within the region (i.e., the source integrated over the region) with the total net outflow across the boundaries defined by the Neumann conditions (i.e., the normal derivative integrated along the whole boundary). It is very important that the algebraic equations derived to model such a problem accurately implement the compatibility condition. If they do not, a net source or sink is very likely to be represented by the set of algebraic equations and no steady-state solution of the equations exists.
References
Ames W F (1977) Nonlinear Partial Differential Equations in Engineering (2nd Edition) Academic Press
Jacobs D A H (1972) The strongly implicit procedure for the numerical solution of parabolic and elliptic partial differential equations Note RD/L/N66/72 Central Electricity Research Laboratory
Stone H L (1968) Iterative solution of implicit approximations of multi-dimensional partial differential equations SIAM J. Numer. Anal. 5 530–558
Weinstein H G, Stone H L and Kwan T V (1969) Iterative procedure for solution of systems of parabolic and elliptic equations in three dimensions Industrial and Engineering Chemistry Fundamentals 8 281–287
Parameters
Compulsory Input Parameters
- 1:
– int64int32nag_int scalar
-
The number of nodes in the first coordinate direction, .
Constraint:
.
- 2:
– int64int32nag_int scalar
-
The number of nodes in the second coordinate direction, .
Constraint:
.
- 3:
– int64int32nag_int scalar
-
The number of nodes in the third coordinate direction, .
Constraint:
.
- 4:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
a, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 5:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
b, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 6:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
c, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 7:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
, the ‘central’ term, in the
th equation of the system
(2), for
,
and
. The elements of
d are checked to ensure that they are nonzero. If any element is found to be zero, the corresponding algebraic equation is assumed to be
. This feature can be used to define the equations for nodes at which, for example, Dirichlet boundary conditions are applied, or for nodes external to the problem of interest, by setting
at appropriate points. The corresponding value of
is set equal to the appropriate value, namely the difference between the prescribed value of
and the current value in the Dirichlet case, or zero at an external point.
- 8:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
e, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 9:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
f, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 10:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
must contain the coefficient of
in the
th equation of the system
(2), for
,
and
. The elements of
g, for
, must be zero after incorporating the boundary conditions, since they involve nodal values from outside the box.
- 11:
– double scalar
-
The iteration acceleration factor. A value of is adequate for most typical problems. However, if convergence is slow, the value can be reduced, typically to or . If divergence is obtained, the value can be increased, typically to , or .
Constraint:
.
- 12:
– int64int32nag_int scalar
-
The iteration number. It must be initialized, but not necessarily to
, before the first call, and should be incremented by one in the calling program for each subsequent call. The function uses this counter to select the appropriate acceleration argument from a sequence of nine, each one being used twice in succession. (Note that the acceleration argument depends on the value of
aparam.)
- 13:
– double array
-
lda, the first dimension of the array, must satisfy the constraint
.
The current residual
on the right-hand side of the
th equation of the system
(2), for
,
and
.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the second dimension of the arrays
a,
b,
c,
d,
e,
f,
g,
r. (An error is raised if these dimensions are not equal.)
The second dimension of the arrays
a,
b,
c,
d,
e,
f,
g,
r,
wrksp1,
wrksp2 and
wrksp3.
Constraint:
.
Output Parameters
- 1:
– double array
-
These residuals store the corresponding components of the solution
of the system
(2), i.e., the changes to be made to the vector
to reduce the residuals supplied.
- 2:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
-
-
| On entry, | , |
| or | , |
| or | . |
-
-
| On entry, | , |
| or | . |
-
-
-
-
| On entry, | . |
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The improvement in accuracy for each iteration, i.e., on each call, depends on the size of the system and on the condition of the update matrix characterised by the seven-diagonal coefficient arrays. The ultimate accuracy obtainable depends on the above factors and on the
machine precision. However, since
nag_pde_3d_ellip_fd_iter (d03ub) works with residuals and the update vector, the calling program can, in most cases where at each iteration all the residuals are usually of about the same size, calculate the residuals from extended precision values of the function, source term and equation coefficients if greater accuracy is required. The rate of convergence obtained with the Strongly Implicit Procedure is not always smooth because of the cyclic use of nine acceleration arguments. The convergence may become slow with very large problems. The final accuracy obtained can be judged approximately from the rate of convergence determined from the changes to the dependent variable
and in particular the change on the last iteration.
Further Comments
The time taken is approximately proportional to for each call.
When used with deferred or defect correction, the residual is calculated in the calling program from a different system of equations to those represented by the seven-point molecule coefficients used by
nag_pde_3d_ellip_fd_iter (d03ub) as the basis of the iterative update procedure. When using deferred correction the overall rate of convergence depends not only on the items detailed in
Accuracy but also on the difference between the two coefficient matrices used.
Convergence may not always be obtained when the problem is very large and/or the coefficients of the equations have widely disparate values. The latter case may be associated with an ill-conditioned matrix.
Example
This example solves Laplace's equation in a rectangular box with a non-uniform grid spacing in the
,
and
coordinate directions and with Dirichlet boundary conditions specifying the function on the surfaces of the box equal to
Note that this is the same problem as that solved in the example for
nag_pde_3d_ellip_fd (d03ec). The differences in the maximum residuals obtained at each iteration between the two test runs are explained by the fact that in
nag_pde_3d_ellip_fd (d03ec) the residual at each node is normalized by dividing by the central coefficient, whereas this normalization has not been used in the example program for
nag_pde_3d_ellip_fd_iter (d03ub).
Open in the MATLAB editor:
d03ub_example
function d03ub_example
fprintf('d03ub example results\n\n');
n = [16 20 24];
b = [ 6 10 15];
delta = b./(n.*(n-1));
for j = 1:n(1)
x(j) = (j*(j-1))*delta(1);
end
for j = 1:n(2)
y(j) = (j*(j-1))*delta(2);
end
for j = 1:n(3)
z(j) = (j*(j-1))*delta(3);
end
a = zeros(n);
b = a; c = a; e = a; f = a; g = a;
q = a; t = a;
aparam = 1;
it = int64(1);
ii = 2:n(1)-1;
jj = 2:n(2)-1;
kk = 2:n(3)-1;
for k = kk
a(ii,jj,k) = 2/((z(k)-z(k-1))*(z(k+1)-z(k-1)));
g(ii,jj,k) = 2/((z(k+1)-z(k))*(z(k+1)-z(k-1)));
end
for j = jj
b(ii,j,kk) = 2/((y(j)-y(j-1))*(y(j+1)-y(j-1)));
f(ii,j,kk) = 2/((y(j+1)-y(j))*(y(j+1)-y(j-1)));
end
for i = ii
c(i,jj,kk) = 2/((x(i)-x(i-1))*(x(i+1)-x(i-1)));
e(i,jj,kk) = 2/((x(i+1)-x(i))*(x(i+1)-x(i-1)));
end
d = -a - b - c - e - f - g;
ex1 = exp((x(1)+1)/y(n(2)));
ex2 = exp((x(n(1))+1)/y(n(2)));
for j = 1:n(2);
cy1 = cos(sqrt(2)*y(j)/y(n(2)));
q(1, j,:) = ex1*cy1*exp((-z(:)-1)/y(n(2)));;
q(n(1),j,:) = ex2*cy1*exp((-z(:)-1)/y(n(2)));;
end
cy1 = cos(sqrt(2)*y(1)/y(n(2)));
cy2 = cos(sqrt(2)*y(n(2))/y(n(2)));
for i = 1:n(1);
ex1 = exp((x(i)+1)/y(n(2)));
q(i,1, :) = ex1*cy1*exp((-z(:)-1)/y(n(2)));;
q(i,n(2),:) = ex1*cy2*exp((-z(:)-1)/y(n(2)));;
end
ez1 = exp((-z(1)-1)/y(n(2)));
ez2 = exp((-z(n(3))-1)/y(n(2)));
for i = 1:n(1);
ex1 = exp((x(i)+1)/y(n(2)));
q(i,:,1) = ex1*cos(sqrt(2)*y(:)/y(n(2)))*ez1;
q(i,:,n(3)) = ex1*cos(sqrt(2)*y(:)/y(n(2)))*ez2;
end
nits = 10;
n = int64(n);
for it = int64(1:nits)
[r] = resid(n(1),n(2),n(3),a,b,c,d,e,f,g,q,t);
[r, ifail] = d03ub( ...
n(1), n(2), n(3), a, b, c, d, e, f, g, aparam, it, r);
t = t + r;
end
for i = 1:n(3)
nrms(i) = norm(r(:,:,i));
end
fprintf('Final residual after %d iterations = %10.1e\n',nits,norm(nrms));
fprintf('\nApproximate solution is:\n\n');
for j=1:4:n(3)
fprintf(' z = %7.4f\n x/y',z(j));
fprintf('%8.2f',x(1:4:n(1)));
for i=1:4:n(2)
fprintf('\n%8.2f',y(i));
fprintf('%8.3f',t(1:4:n(1),i,j));
end
fprintf('\n\n');
end
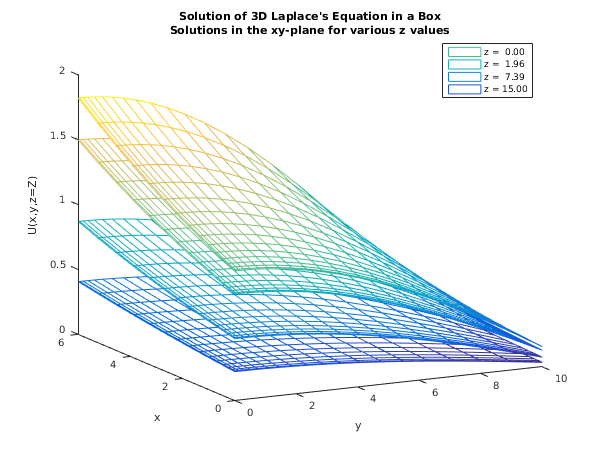
fig1 = figure;
hold on
mesh(y,x,t(:,:,1));
mesh(y,x,t(:,:,9));
mesh(y,x,t(:,:,17));
mesh(y,x,t(:,:,24));
z1 = sprintf('z = %5.2f',z(1));
z2 = sprintf('z = %5.2f',z(9));
z3 = sprintf('z = %5.2f',z(17));
z4 = sprintf('z = %5.2f',z(24));
title({'Solution of 3D Laplace''s Equation in a Box',
'Solutions in the xy-plane for various z values'});
xlabel('y');
ylabel('x');
zlabel('U(x,y,z=Z)');
legend(z1,z2,z3,z4);
view(-27,16);
hold off
function [r] = resid(n1,n2,n3,a,b,c,d,e,f,g,q,t)
r = zeros(n1, n2, n3);
for k = 1:n3
for j = 1:n2
for i = 1:n1
if (d(i,j,k) ~= 0)
r(i,j,k) = q(i,j,k) - a(i,j,k)*t(i,j,k-1) - b(i,j,k)*t(i,j-1,k) - ...
c(i,j,k)*t(i-1,j,k) - d(i,j,k)*t(i,j,k) - ...
e(i,j,k)*t(i+1,j,k) - f(i,j,k)*t(i,j+1,k) - ...
g(i,j,k)*t(i,j,k+1);
else
r(i,j,k) = q(i,j,k) - t(i,j,k);
end
end
end
end
d03ub example results
Final residual after 10 iterations = 1.4e-04
Approximate solution is:
z = 0.0000
x/y 0.00 0.50 1.80 3.90
0.00 1.000 1.051 1.197 1.477
0.53 0.997 1.048 1.194 1.473
1.89 0.964 1.014 1.154 1.424
4.11 0.836 0.879 1.001 1.235
7.16 0.530 0.557 0.634 0.783
z = 0.5435
x/y 0.00 0.50 1.80 3.90
0.00 0.947 0.996 1.134 1.399
0.53 0.944 0.993 1.131 1.395
1.89 0.913 0.960 1.093 1.349
4.11 0.792 0.833 0.948 1.170
7.16 0.502 0.528 0.601 0.741
z = 1.9565
x/y 0.00 0.50 1.80 3.90
0.00 0.822 0.864 0.984 1.215
0.53 0.820 0.862 0.982 1.211
1.89 0.793 0.834 0.949 1.171
4.11 0.688 0.723 0.823 1.016
7.16 0.436 0.458 0.522 0.644
z = 4.2391
x/y 0.00 0.50 1.80 3.90
0.00 0.654 0.688 0.784 0.967
0.53 0.653 0.686 0.781 0.964
1.89 0.631 0.664 0.756 0.932
4.11 0.547 0.575 0.655 0.808
7.16 0.347 0.365 0.415 0.512
z = 7.3913
x/y 0.00 0.50 1.80 3.90
0.00 0.478 0.502 0.572 0.705
0.53 0.476 0.501 0.570 0.703
1.89 0.460 0.484 0.551 0.680
4.11 0.399 0.420 0.478 0.590
7.16 0.253 0.266 0.303 0.374
z = 11.4130
x/y 0.00 0.50 1.80 3.90
0.00 0.319 0.336 0.382 0.472
0.53 0.319 0.335 0.381 0.470
1.89 0.308 0.324 0.369 0.455
4.11 0.267 0.281 0.320 0.395
7.16 0.169 0.178 0.203 0.250
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015
