| On entry, | or , |
| or | , |
| or | , |
| or | , |
| or | , or , |
| or | the mesh points , for , are not in strictly increasing order. |
Open in the MATLAB editor: d03pz_example
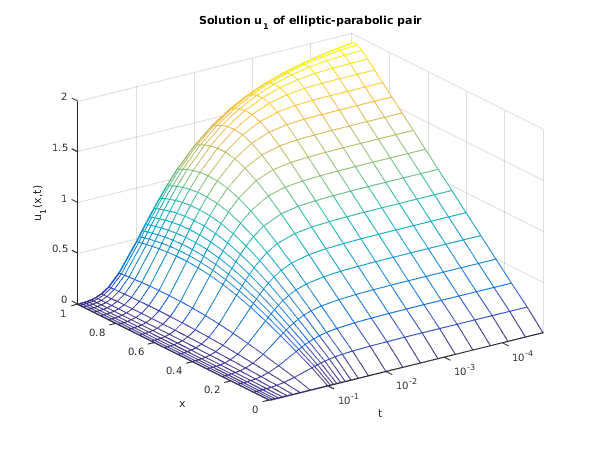
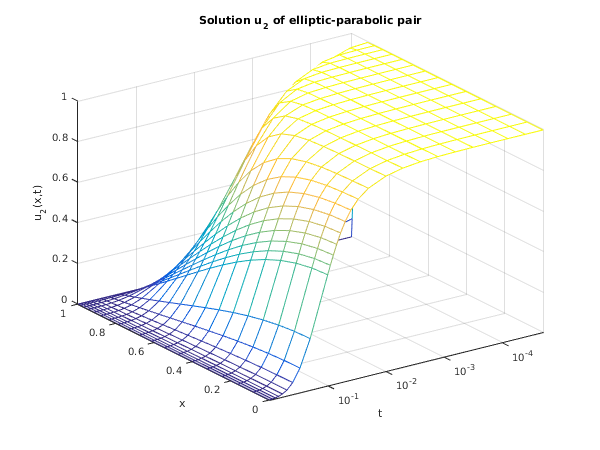
function d03pz_example fprintf('d03pz example results\n\n'); % Solution of an elliptic-parabolic pair of PDEs. global alpha; % Set values for problem parameters. npde = 2; % Number of points on calculation mesh, and on interpolated mesh. npts = 20; intpts = 6; itype = int64(1); neqn = npde*npts; lisave = neqn + 24; nwk = (10 + 6*npde)*neqn; lrsave = nwk + (21 + 3*npde)*npde + 7*npts + 54; % Define some arrays. rsave = zeros(lrsave, 1); u = zeros(npde, npts); uinterp = zeros(npde, intpts, itype); x = zeros(npts, 1); isave = zeros(lisave, 1, 'int64'); cwsav = {''; ''; ''; ''; ''; ''; ''; ''; ''; ''}; lwsav = false(100, 1); iwsav = zeros(505, 1, 'int64'); rwsav = zeros(1100, 1); % Set up the points on the interpolation grid. xinterp = [0.0 0.4 0.6 0.8 0.9 1.0]; acc = 1.0e-3; alpha = 1; itrace = int64(0); itask = int64(1); % Use cylindrical polar coordinates. m = int64(1); % We run through the calculation twice; once to output the interpolated % results, and once to store the results for plotting. niter = [5, 28]; % Prepare to store plotting results. tsav = zeros(niter(2), 1); usav = zeros(2, niter(2), npts); isav = 0; for icalc = 1:2 % Set spatial mesh points. piby2 = pi/2; hx = piby2/(npts-1); x = sin(0:hx:piby2); % Set initial conditions. ts = 0; tout = 1e-5; % Set the initial values. [u] = uinit(x, npts); % Start the integration in time. ind = int64(0); % Counter for saved results. isav = 0; % Loop over endpoints for the integration. % Set itask = 1: normal computation of output values at t = tout. for iter = 1:niter(icalc) %Set the endpoint. if icalc == 1 tout = 10.0*tout; else if iter < 10 tout = 2*tout; else if iter == 10 tout = 0.01; else if iter < 20 tout = tout + 0.01; else tout = tout + 0.1; end end end end % The first time this is called, ind is 0, which (re)starts the % integration in time. On exit, ind is set to 1; using this value % on a subsequent call continues the integration. This means that % only tout and ifail should be reset between calls. [ts, u, rsave, isave, ind, user, cwsav, lwsav, iwsav, rwsav, ifail] = ... d03pc(... m, ts, tout, @pdedef, @bndary, u, x, acc, rsave, isave, itask, ... itrace, ind, cwsav, lwsav, iwsav, rwsav); if icalc == 1 % Output interpolation points first time through. if iter == 1 fprintf([' accuracy requirement = %12.5e\n', ... ' parameter alpha = %12.3e\n'], acc, alpha); fprintf(' t / x '); fprintf('%8.4f', xinterp(1:intpts)); fprintf('\n\n'); end % Call d03pz to do interpolation of results onto coarser grid. [uinterp, ifail] = d03pz( ... m, u, x, xinterp, itype); % Output interpolated results for this time step. fprintf('%7.4f u(1)', tout); fprintf('%8.4f', uinterp(1,1:intpts,1)); fprintf('\n%13s','u(2)'); fprintf('%8.4f', uinterp(2,1:intpts,1)); fprintf('\n\n'); else % Save this timestep, and this set of results. isav = isav+1; tsav(isav) = ts; usav(1:2,isav,1:npts) = u(1:2,1:npts); end end if icalc == 1 % Output some statistics. fprintf([' Number of integration steps in time = %6d\n', ... ' Number of function evaluations = %6d\n', ... ' Number of Jacobian evaluations = %6d\n', ... ' Number of iterations = %6d\n'], ... isave(1), isave(2), isave(3), isave(5)); else % Plot results. fig1 = figure; plot_results(x, tsav, squeeze(usav(1,:,:)), 'u_1'); fig2 = figure; plot_results(x, tsav, squeeze(usav(2,:,:)), 'u_2'); end end function [p, q, r, ires, user] = pdedef(npde, t, x, u, ux, ires, user) % Evaluate Pij, Qi and Ri which define the system of PDEs. global alpha; p = zeros(npde,npde); q = zeros(npde,1); r = zeros(npde,1); q(1) = 4*alpha*(u(2) + x*ux(2)); r(1) = x*ux(1); r(2) = ux(2) - u(1)*u(2); p(2,2) = 1 - x*x; function [beta, gamma, ires, user] = bndary(npde, t, u, ux, ibnd, ires, user) % Evaluate beta and gamma to define the boundary conditions. if (ibnd == 0) beta(1) = 0; beta(2) = 1; gamma(1) = u(1); gamma(2) = -u(1)*u(2); else beta(1) = 1; beta(2) = 0; gamma(1) = -u(1); gamma(2) = u(2); end function [u] = uinit(x, npts) % Set initial values for solution. global alpha; for i = 1:npts u(1,i) = 2*alpha*x(i); u(2,i) = 1; end function plot_results(x, t, u, ident) % Plot array as a mesh. mesh(x, t, u); set(gca, 'YScale', 'log'); set(gca, 'YTick', [0.00001 0.0001 0.001 0.01 0.1 1]); set(gca, 'YMinorGrid', 'off'); set(gca, 'YMinorTick', 'off'); % Label the axes, and set the title. xlabel('x'); ylabel('t'); zlabel([ident,'(x,t)']); title({['Solution ',ident,' of elliptic-parabolic pair'], ... 'using method of lines and BDF'}); title(['Solution ',ident,' of elliptic-parabolic pair']); % Set the axes limits tight to the x and y range. axis([x(1) x(end) t(1) t(end)]); % Set the view to something nice (determined empirically). view(-125, 30);
d03pz example results
accuracy requirement = 1.00000e-03
parameter alpha = 1.000e+00
t / x 0.0000 0.4000 0.6000 0.8000 0.9000 1.0000
0.0001 u(1) 0.0000 0.8008 1.1988 1.5990 1.7958 1.8485
u(2) 0.9997 0.9995 0.9994 0.9988 0.9663 -0.0000
0.0010 u(1) 0.0000 0.7982 1.1940 1.5841 1.7179 1.6734
u(2) 0.9969 0.9952 0.9937 0.9484 0.6385 -0.0000
0.0100 u(1) 0.0000 0.7676 1.1239 1.3547 1.3635 1.2830
u(2) 0.9627 0.9495 0.8754 0.5537 0.2908 -0.0000
0.1000 u(1) 0.0000 0.3908 0.5007 0.5297 0.5120 0.4744
u(2) 0.5468 0.4299 0.2995 0.1479 0.0724 -0.0000
1.0000 u(1) 0.0000 0.0007 0.0008 0.0008 0.0008 0.0007
u(2) 0.0010 0.0007 0.0005 0.0002 0.0001 -0.0000
Number of integration steps in time = 78
Number of function evaluations = 378
Number of Jacobian evaluations = 25
Number of iterations = 190