Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lrsave was removed from the interface |
nag_pde_1d_parab_coll_interp (d03py) is an interpolation function for evaluating the solution of a system of partial differential equations (PDEs), or the PDE components of a system of PDEs with coupled ordinary differential equations (ODEs), at a set of user-specified points. The solution of a system of equations can be computed using
nag_pde_1d_parab_coll (d03pd) or
nag_pde_1d_parab_dae_coll (d03pj) on a set of mesh points;
nag_pde_1d_parab_coll_interp (d03py) can then be employed to compute the solution at a set of points other than those originally used in
nag_pde_1d_parab_coll (d03pd) or
nag_pde_1d_parab_dae_coll (d03pj). It can also evaluate the first derivative of the solution.
Polynomial interpolation is used between each of the break-points
, for
. When the derivative is needed (
), the array
must not contain any of the break-points, as the method, and consequently the interpolation scheme, assumes that only the solution is continuous at these points.
None.
None.
function d03py_example
fprintf('d03py example results\n\n');
npde = 2;
intpts = 6;
nbkpts = 10;
npoly = int64(3);
npts = (nbkpts-1)*npoly + 1;
lisave = npde*npts + 24;
rsave = zeros(4000, 1);
u = zeros(npde, npts);
isave = zeros(lisave, 1, 'int64');
lwsav = false(100, 1);
iwsav = zeros(505, 1, 'int64');
rwsav = zeros(1100, 1);
cwsav = {''; ''; ''; ''; ''; ''; ''; ''; ''; ''};
xinterp = [-1:0.4:1];
niter = 20;
tsav = zeros(niter, 1);
usav = zeros(2, niter, npts);
isav = 0;
hx = 2/(nbkpts-1);
xbkpts = [-1:hx:1];
m = int64(0);
ts = 0.0;
tout = 0.1e-4;
acc = 1.0e-4;
itask = int64(1);
itrace = int64(0);
ind0 = int64(0);
alpha = -log(tout)/(niter-1);
fprintf('polynomial degree = %4d no. of elements = %4d\n', npoly, nbkpts-1);
fprintf('accuracy requirement = %10.3e number of points = %5d', acc, npts);
fprintf('\n\n t / x ');
fprintf('%8.4f', xinterp);
fprintf('\n\n');
for iter = 1:niter
tout = exp(alpha*(iter - niter));
[ts, u, x, rsave, isave, ind, user, cwsav, lwsav, iwsav, rwsav, ifail] = ...
d03pd( ...
m, ts, tout, @pdedef, ...
@bndary, u, xbkpts, npoly, @uinit, ...
acc, rsave, isave, itask, itrace, ind0, ...
cwsav, lwsav, iwsav, rwsav);
itype = int64(1);
[uinterp, rsave, ifail] = d03py( ...
u, xbkpts, npoly, xinterp, itype, rsave);
fprintf('%7.4f u(1)', ts);
fprintf('%8.4f', uinterp(1,:,1));
fprintf('\n u(2)');
fprintf('%8.4f', uinterp(2,:,1));
fprintf('\n\n');
isav = isav+1;
tsav(isav) = ts;
usav(1:2,isav,1:npts) = u(1:2,1:npts);
end
fprintf(' Number of integration steps in time = %6d\n', isave(1));
fprintf(' Number of function evaluations = %6d\n', isave(2));
fprintf(' Number of Jacobian evaluations = %6d\n', isave(3));
fprintf(' Number of iterations = %6d\n', isave(5));
fig1 = figure;
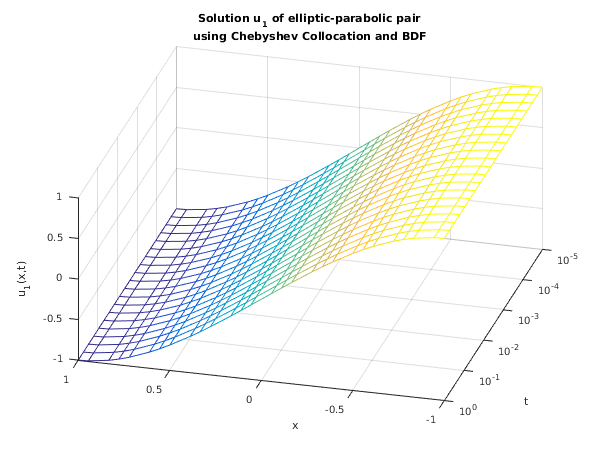
plot_results(x, tsav, squeeze(usav(1,:,:)), 'u_1');
fig2 = figure;
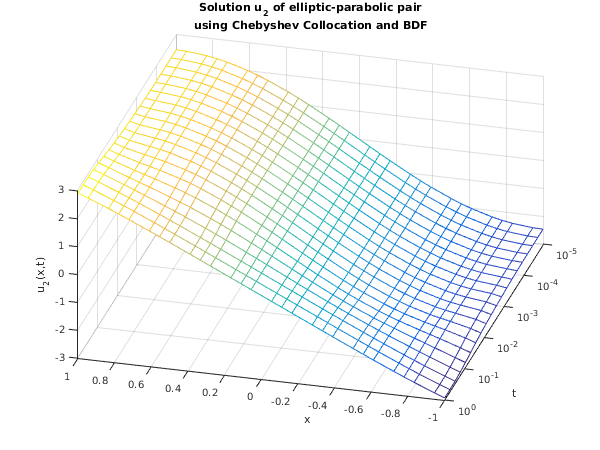
plot_results(x, tsav, squeeze(usav(2,:,:)), 'u_2');
function [p, q, r, ires, user] = pdedef(npde, t, x, nptl, u, ux, ires, user)
p = zeros(npde, npde, nptl);
q = zeros(npde, nptl);
r = zeros(npde, nptl);
for i = 1:double(nptl)
q(1,i) = u(2,i);
q(2,i) = u(1,i)*ux(2,i) - ux(1,i)*u(2,i);
r(1,i) = ux(1,i);
r(2,i) = ux(2,i);
p(2,2,i) = 1;
end;
function [beta, gamma, ires, user] = bndary(npde, t, u, ux, ibnd, ires, user)
beta = zeros(npde, 1);
gamma = zeros(npde, 1);
beta(1) = 1;
beta(2) = 0;
gamma(1) = 0;
if (ibnd == 0)
gamma(2) = u(1) - 1;
else
gamma(2) = u(1) + 1;
end
function [u, user] = uinit(npde, npts, x, user)
u = zeros(npde, npts);
piby2 = pi/2;
u(1,:) = -sin(piby2*x);
u(2,:) = -piby2*piby2*u(1,:);
function plot_results(x, t, u, ident)
mesh(x, t, u);
set(gca, 'YScale', 'log');
set(gca, 'YTick', [0.00001 0.0001 0.001 0.01 0.1 1]);
set(gca, 'YMinorGrid', 'off');
set(gca, 'YMinorTick', 'off');
xlabel('x');
ylabel('t');
zlabel([ident,'(x,t)']);
title({['Solution ',ident,' of elliptic-parabolic pair'], ...
'using Chebyshev Collocation and BDF'});
axis([x(1) x(end) t(1) t(end)]);
view(-165, 44);