nag_pde_1d_parab_euler_hll (d03pw) calculates a numerical flux function using a modified HLL (Harten–Lax–van Leer) Approximate Riemann Solver for the Euler equations in conservative form. It is designed primarily for use with the upwind discretization schemes
nag_pde_1d_parab_convdiff (d03pf),
nag_pde_1d_parab_convdiff_dae (d03pl) or
nag_pde_1d_parab_convdiff_remesh (d03ps), but may also be applicable to other conservative upwind schemes requiring numerical flux functions.
nag_pde_1d_parab_euler_hll (d03pw) calculates a numerical flux function at a single spatial point using a modified HLL (Harten–Lax–van Leer) Approximate Riemann Solver (see
Toro (1992),
Toro (1996) and
Toro et al. (1994)) for the Euler equations (for a perfect gas) in conservative form. You must supply the
left and
right solution values at the point where the numerical flux is required, i.e., the initial left and right states of the Riemann problem defined below. In
nag_pde_1d_parab_convdiff (d03pf),
nag_pde_1d_parab_convdiff_dae (d03pl) and
nag_pde_1d_parab_convdiff_remesh (d03ps), the left and right solution values are derived automatically from the solution values at adjacent spatial points and supplied to the function argument
numflx from which you may call
nag_pde_1d_parab_euler_hll (d03pw).
The Euler equations for a perfect gas in conservative form are:
with
where
is the density,
is the momentum,
is the specific total energy and
is the (constant) ratio of specific heats. The pressure
is given by
where
is the velocity.
The function calculates an approximation to the numerical flux function
, where
and
are the left and right solution values, and
is the intermediate state
arising from the similarity solution
of the Riemann problem defined by
with
and
as in
(2), and initial piecewise constant values
for
and
for
. The spatial domain is
, where
is the point at which the numerical flux is required.
Toro E F (1992) The weighted average flux method applied to the Euler equations Phil. Trans. R. Soc. Lond. A341 499–530
Toro E F, Spruce M and Spears W (1994) Restoration of the contact surface in the HLL Riemann solver J. Shock Waves 4 25–34
None.
nag_pde_1d_parab_euler_hll (d03pw) performs an exact calculation of the HLL (Harten–Lax–van Leer) numerical flux function, and so the result will be accurate to
machine precision.
nag_pde_1d_parab_euler_hll (d03pw) must only be used to calculate the numerical flux for the Euler equations in exactly the form given by
(2), with
and
containing the left and right values of
and
, for
, respectively. The time taken is independent of the input arguments.
This example uses
nag_pde_1d_parab_convdiff_dae (d03pl) and
nag_pde_1d_parab_euler_hll (d03pw) to solve the Euler equations in the domain
for
with initial conditions for the primitive variables
,
and
given by
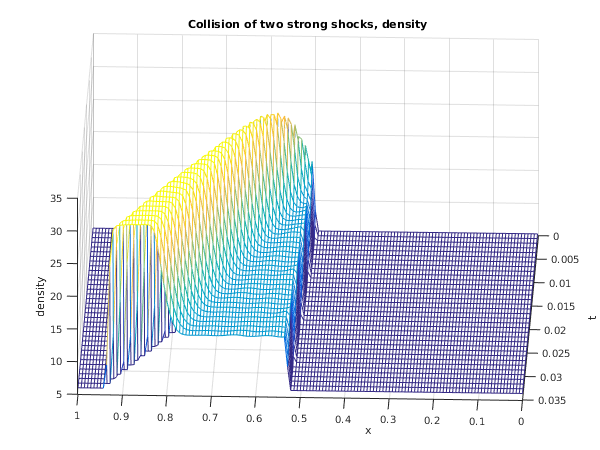
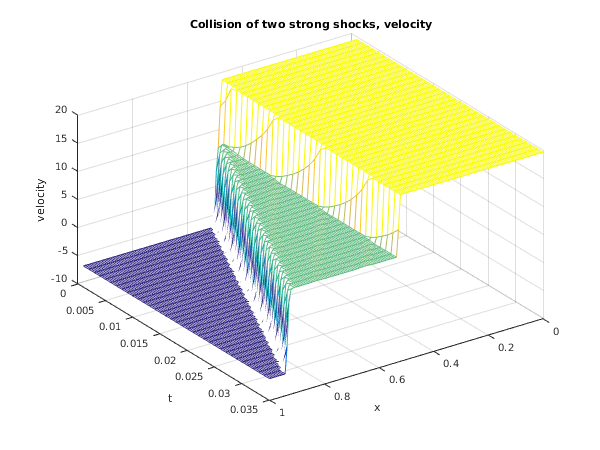
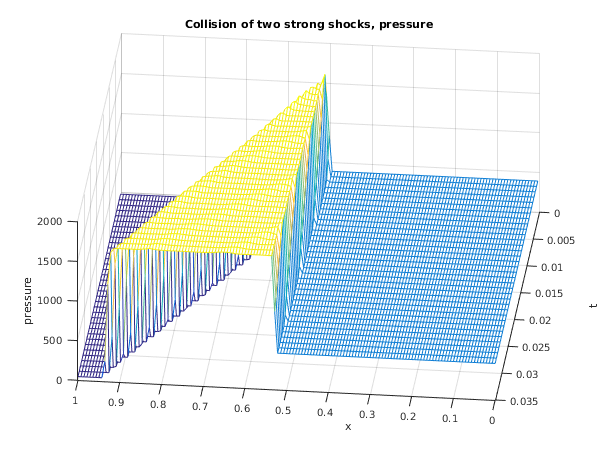
This test problem is taken from
Toro (1996) and its solution represents the collision of two strong shocks travelling in opposite directions, consisting of a left facing shock (travelling slowly to the right), a right travelling contact discontinuity and a right travelling shock wave. There is an exact solution to this problem (see
Toro (1996)) but the calculation is lengthy and has therefore been omitted.
function d03pw_example
fprintf('d03pw example results\n\n');
global gamma rl0 rr0 ul0 ur0 el0 er0;
alpha_l = 460.894;
alpha_r = 46.095;
beta_l = 19.5975;
beta_r = 6.19633;
gamma = 1.4;
rl0 = 5.99924;
rr0 = 5.99242;
ul0 = 117.5701059;
ur0 = -37.1310118186;
el0 = alpha_l/(gamma-1) + rl0*beta_l^2/2;
er0 = alpha_r/(gamma-1) + rr0*beta_r^2/2;
npde = int64(3);
npts = int64(141);
ncode = int64(0);
nxi = int64(0);
neqn = npde*npts+ncode;
ts = 0;
xi = [];
itol = int64(1);
atol = [0.005];
rtol = [0.0005];
norm_p = '2';
laopt = 'B';
algopt = zeros(30,1);
algopt(1) = 2;
algopt(6) = 2;
algopt(7) = 2;
algopt(13) = 0.005;
rsave = zeros(21000, 1);
isave = zeros(25700, 1, 'int64');
itask = int64(1);
itrace = int64(0);
ind = int64(0);
dx = 1/(double(npts)-1);
x = [0:dx:1];
u = uvinit(x);
u1sol = zeros(35,npts);
u2sol = zeros(35,npts);
u3sol = zeros(35,npts);
xsol = zeros(35,npts);
tsol = zeros(35,npts);
for j=1:35
tout = 0.001*j;
[ts, u, rsave, isave, ind, ifail] = ...
d03pl( ...
npde, ts, tout, 'd03plp', @numflx, @bndary, u, x, ncode, ...
'd03pek', xi, rtol, atol, itol, norm_p, laopt, ...
algopt, rsave, isave, itask, itrace, ind,'nxi',nxi);
xsol(j,:) = x;
tsol(j,:) = ts;
u1sol(j,:) = u(1,:);
u2sol(j,:) = u(2,:)./u(1,:);
u3sol(j,:) = 0.4*u(1,:).*(u(3,:)./u(1,:)-u2sol(j,:).^2/2);
end
nsteps = 50*((isave(1)+25)/50);
nfuncs = 50*((isave(2)+25)/50);
njacs = isave(3);
niters = isave(5);
fprintf('\n Number of time steps (nearest 50) = %6d\n',nsteps);
fprintf(' Number of function evaluations (nearest 50) = %6d\n',nfuncs);
fprintf(' Number of Jacobian evaluations (nearest 1) = %6d\n',njacs);
fprintf(' Number of iterations (nearest 1) = %6d\n',niters);
fig1=figure;
mesh(xsol,tsol,u1sol);
title('Collision of two strong shocks, density');
xlabel('x');
ylabel('t');
zlabel('density');
view(182,40);
fig2=figure;
mesh(xsol,tsol,u2sol);
title('Collision of two strong shocks, velocity');
xlabel('x');
ylabel('t');
zlabel('velocity');
view(145,40);
fig3=figure;
mesh(xsol,tsol,u3sol);
title('Collision of two strong shocks, pressure');
xlabel('x');
ylabel('t');
zlabel('pressure');
view(-174,50);
function [g, iresout] = bndary(npde, npts, t, x, u, ncode, ...
v, vdot, ibnd, ires)
global rl0 rr0 ul0 ur0 el0 er0;
if (ibnd == 0)
g(1) = u(1,1) - rl0;
g(2) = u(2,1) - ul0;
g(3) = u(3,1) - el0;
else
g(1) = u(1,npts) - rr0;
g(2) = u(2,npts) - ur0;
g(3) = u(3,npts) - er0;
end
iresout = ires;
function [flux, ires] = numflx(npde, t, x, ncode, v, uleft, uright, ires)
global gamma;
[flux, ifail] = d03pw( ...
uleft, uright, gamma);
function [u] = uvinit(x)
global rl0 rr0 ul0 ur0 el0 er0;
n = size(x,2);
u = zeros(3,n);
for i = 1:n
if x(i)<1/2
u(1,i) = rl0;
u(2,i) = ul0;
u(3,i) = el0;
elseif x(i)== 1/2
u(1,i) = (rl0+rr0)/2;
u(2,i) = (ul0+ur0)/2;
u(3,i) = (el0+er0)/2;
else
u(1,i) = rr0;
u(2,i) = ur0;
u(3,i) = er0;
end
end