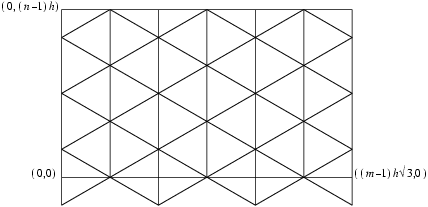
nag_pde_2d_triangulate (d03ma) begins with a uniform triangular grid as shown in Figure 1 and assumes that the region to be triangulated lies within the rectangle given by the inequalities

0 < x < \sqrt{3} (m - 1) h, 0 < y < (n - 1) h .

This rectangle is drawn in bold in Figure 1. The region is specified by the isin which must determine whether any given point

(x, y)

lies in the region. The uniform grid is processed column-wise, with

(x_{1}, y_{1})

preceding

(x_{2}, y_{2})

x_{1} < x_{2}

x_{1} = x_{2}

y_{1} < y_{2}

. Points near the boundary are moved onto it and points well outside the boundary are omitted. The direction of movement is chosen to avoid pathologically thin triangles. The points accepted are numbered in exactly the same order as the corresponding points of the uniform grid were scanned. The output consists of the

x, y

coordinates of all grid points and integers indicating whether they are internal and to which other points they are joined by triangle sides.

The mesh size

h

must be chosen small enough for the essential features of the region to be apparent from testing all points of the original uniform grid for being inside the region. For instance if any hole is within

2 h

of another hole or the outer boundary then a triangle may be found with all vertices within

\frac{1}{2} h

of a boundary. Such a triangle is taken to be external to the region so the effect will be to join the hole to another hole or to the external region.

Further details of the algorithm are given in the references.

Figure 1

References

Reid J K (1970) Fortran subroutines for the solutions of Laplace's equation over a general routine in two dimensions Harwell Report TP422

Reid J K (1972) On the construction and convergence of a finite-element solution of Laplace's equation J. Instr. Math. Appl. 9 1–13

Parameters

Compulsory Input Parameters

1: $h$ – double scalar

h

, the required length for the sides of the triangles of the uniform mesh.

2: $m$ – int64int32nag_int scalar

3: $n$ – int64int32nag_int scalar

Values

m

and

n

such that all points

(x, y)

inside the region satisfy the inequalities

\begin{array}{l} 0 \leq x \leq \sqrt{3} (m - 1) h, \\ 0 \leq y \leq (n - 1) h . \end{array}

Constraint:

m = n > 2

4: $nb$ – int64int32nag_int scalar

The number of times a triangle side is bisected to find a point on the boundary. A value of

10

is adequate for most purposes (see Accuracy).

Constraint:

nb \geq 1

5: $sdindx$ – int64int32nag_int scalar

An upper bound on the number of points in the triangulation. The actual value will be returned in npts.

6: $isin$ – function handle or string containing name of m-file

isin must return the value

1

if the given point (x,y) lies inside the region, and

0

if it lies outside.

[result] = isin(x, y)

Input Parameters

1: $x$ – double scalar
2: $y$ – double scalar: The coordinates of the given point.

Output Parameters

1: $result$ – int64int32nag_int scalar: The value $1$ if the given point (x,y) lies inside the region, and $0$ if it lies outside.

Optional Input Parameters

None.

Output Parameters

1: $npts$ – int64int32nag_int scalar: The number of points in the triangulation.
2: $places (2, sdindx)$ – double array: The $x$ and $y$ coordinates respectively of the $i$ th point of the triangulation.
3: $indx (4, sdindx)$ – int64int32nag_int array: $indx (1, i)$ contains $i$ if point $i$ is inside the region and $- i$ if it is on the boundary. For each triangle side between points $i$ and $j$ with $j > i$ , $indx (k, i)$ , $k > 1$ , contains $j$ or $- j$ according to whether point $j$ is internal or on the boundary. There can never be more than three such points. If there are less, then some values $indx (k, i)$ , $k > 1$ , are zero.
4: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$: sdindx is too small.

$ifail = 2$: A point inside the region violates one of the constraints (see arguments m and n).

$ifail = 3$: sddist is too small.

$ifail = 4$: $m \leq 2$ .

$ifail = 5$: $n \leq 2$ .

$ifail = 6$: $nb \leq 0$ .

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

Points are moved onto the boundary by bisecting a triangle side nb times. The accuracy is therefore

h \times 2^{- nb}

Further Comments

The time taken is approximately proportional to

m \times n

Example

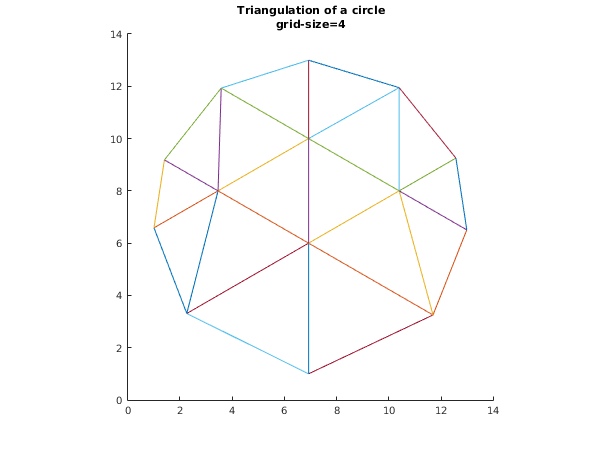
The following program triangulates the circle with centre

(7.0, 7.0)

and radius

6.0

using a basic grid size

h = 4.0

Open in the MATLAB editor: d03ma_example

function d03ma_example


fprintf('d03ma example results\n\n');

h = 4;
m = int64(3);
n = int64(5);
nb = int64(10);
sdindx = int64(100);
[npts, places, index, ifail] = d03ma( ...
                                      h, m, n, nb, sdindx, @isin);

fprintf('Number of points = %4d\n',npts);

fig1 = figure;
k = 0;
hold on
for i = 1:npts
  for j=2:4
    % lines connecting from node i
     if(index(j,i)~=0)
       k = k + 1;
       l = abs(index(j,i));
       x(1) = places(1,i);
       x(2) = places(1,l);
       y(1) = places(2,i);
       y(2) = places(2,l);
       plot(x,y) 
     end
  end
end
axis square;
title({'Triangulation of a circle','grid-size=4'});
hold off;

fprintf('Number of edges  = %4d\n',k);



function result = isin(x,y)
  if ((x-7)^2+(y-7)^2 <= 36)
    result = int64(1);
  else
    result = int64(0);
  end

d03ma example results

Number of points =   14
Number of edges  =   29

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox