None.
Open in the MATLAB editor: d02uc_example
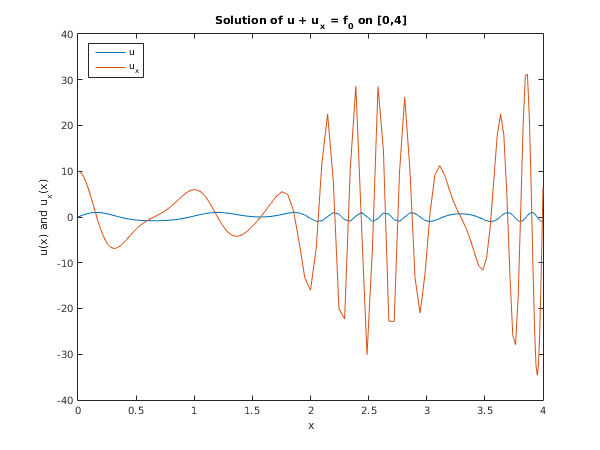
function d02uc_example fprintf('d02uc example results\n\n'); % On [0,4], Solve u + ux = f0(x); u(0) = 0 % where f) is such that u(x) = sin(10xcos^2x). % Set up Chebyshev grid on [a,b] a = 0; b = 4; n = int64(128); [x, ifail] = d02uc(n, a, b); % Get Chebyshev coeficients on grid for f0(x) = 1. z = 10*x.*cos(x).^2; f0 = sin(z) - 10*cos(x).^2.*cos(10*x.*cos(x).^2).*(2*x.*tan(x)-1); [f0_c, ifail] = d02ua(n, f0); % Set up problem definition for u + ux = f0 [(1 1).(u ux) = f0] f = [1, 1]; % subject to u(a) = 0 [(1 0).(u ux)(a) = 0] y = [a]; B = [1, 0]; beta = 0; % Solve in coefficient space using f0_c for rhs. [B, f, uc, resid, ifail] = d02ue(... n, a, b, f0_c, B, y, beta, f); % Transform solution and derivative back to real space. [u, ifail] = d02ub(... n, a, b, int64(0), uc(:, 1)); [ux, ifail] = d02ub(... n, a, b, int64(1), uc(:, 2)); maxerr = max(abs(u - sin(z))); fprintf('With n = %4d, maximum error in solution = %13.2e\n',n,maxerr); % Plot solution fig1 = figure; plot(x,u,x,ux); title('Solution of u + u_x = f_0 on [0,4]'); xlabel('x'); ylabel('u(x) and u_x(x)'); legend('u','u_x','Location','Northwest');
d02uc example results With n = 128, maximum error in solution = 5.33e-09
