hide long namesshow long names
hide short namesshow short names
Integer type:  int32  int64  nag_int  show int32  show int32  show int64  show int64  show nag_int  show nag_int
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox

NAG Toolbox: nag_ode_withdraw_bvp_coll_nlin (d02tk)

▸▿ Contents

    1  Purpose
    2  Syntax
    3  Description
    4  References
▸▿ 5  Parameters
    6  Error Indicators and Warnings
    7  Accuracy
    8  Further Comments
    9  Example

Purpose

nag_ode_bvp_coll_nlin (d02tk) solves a general two-point boundary value problem for a nonlinear mixed order system of ordinary differential equations.
Note: this function is scheduled to be withdrawn, please see d02tk in Advice on Replacement Calls for Withdrawn/Superseded Routines..

Syntax

[rcomm, icomm, ifail] = d02tk(ffun, fjac, gafun, gbfun, gajac, gbjac, guess, rcomm, icomm)
[rcomm, icomm, ifail] = nag_ode_withdraw_bvp_coll_nlin(ffun, fjac, gafun, gbfun, gajac, gbjac, guess, rcomm, icomm)

Description

nag_ode_bvp_coll_nlin (d02tk) and its associated functions (nag_ode_bvp_coll_nlin_setup (d02tv), nag_ode_bvp_coll_nlin_contin (d02tx), nag_ode_bvp_coll_nlin_interp (d02ty) and nag_ode_bvp_coll_nlin_diag (d02tz)) solve the two-point boundary value problem for a nonlinear mixed order system of ordinary differential equations
y1m1 x = f1 x,y1,y11,…,y1m1-1,y2,…,ynmn-1 y2m2 x = f2 x,y1,y11,…,y1m1-1,y2,…,ynmn-1 ⋮ ynmn x = fn x,y1,y11,…,y1m1-1,y2,…,ynmn-1  
over an interval a,b subject to p (>0) nonlinear boundary conditions at a and q (>0) nonlinear boundary conditions at b, where p+q = ∑ i=1 n mi . Note that yi m x is the mth derivative of the ith solution component. Hence yi 0 x=yix. The left boundary conditions at a are defined as
gizya=0,  i=1,2,…,p,  
and the right boundary conditions at b as
g-jzyb=0,  j=1,2,…,q,  
where y=y1,y2,…,yn and
zyx = y1x, y11 x ,…, y1m1-1 x ,y2x,…, ynmn-1 x .  
First, nag_ode_bvp_coll_nlin_setup (d02tv) must be called to specify the initial mesh, error requirements and other details. Note that the error requirements apply only to the solution components y1,y2,…,yn and that no error control is applied to derivatives of solution components. (If error control is required on derivatives then the system must be reduced in order by introducing the derivatives whose error is to be controlled as new variables. See Further Comments in nag_ode_bvp_coll_nlin_setup (d02tv).) Then, nag_ode_bvp_coll_nlin (d02tk) can be used to solve the boundary value problem. After successful computation, nag_ode_bvp_coll_nlin_diag (d02tz) can be used to ascertain details about the final mesh and other details of the solution procedure, and nag_ode_bvp_coll_nlin_interp (d02ty) can be used to compute the approximate solution anywhere on the interval a,b.
A description of the numerical technique used in nag_ode_bvp_coll_nlin (d02tk) is given in Description in nag_ode_bvp_coll_nlin_setup (d02tv).
nag_ode_bvp_coll_nlin (d02tk) can also be used in the solution of a series of problems, for example in performing continuation, when the mesh used to compute the solution of one problem is to be used as the initial mesh for the solution of the next related problem. nag_ode_bvp_coll_nlin_contin (d02tx) should be used in between calls to nag_ode_bvp_coll_nlin (d02tk) in this context.
See Further Comments in nag_ode_bvp_coll_nlin_setup (d02tv) for details of how to solve boundary value problems of a more general nature.
The functions are based on modified versions of the codes COLSYS and COLNEW (see Ascher et al. (1979) and Ascher and Bader (1987)). A comprehensive treatment of the numerical solution of boundary value problems can be found in Ascher et al. (1988) and Keller (1992).

References

Ascher U M and Bader G (1987) A new basis implementation for a mixed order boundary value ODE solver SIAM J. Sci. Stat. Comput. 8 483–500
Ascher U M, Christiansen J and Russell R D (1979) A collocation solver for mixed order systems of boundary value problems Math. Comput. 33 659–679
Ascher U M, Mattheij R M M and Russell R D (1988) Numerical Solution of Boundary Value Problems for Ordinary Differential Equations Prentice–Hall
Keller H B (1992) Numerical Methods for Two-point Boundary-value Problems Dover, New York

Parameters

Compulsory Input Parameters

1:     ffun – function handle or string containing name of m-file
ffun must evaluate the functions fi for given values x,zyx.
[f] = ffun(x, y, neq, m)

Input Parameters

1:     x – double scalar
x, the independent variable.
2:     yneq* – double array
yij contains yi j x, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 x=yix.
3:     neq – int64int32nag_int scalar
The number of differential equations.
4:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.

Output Parameters

1:     fneq – double array
fi must contain fi, for i=1,2,…,neq.
2:     fjac – function handle or string containing name of m-file
fjac must evaluate the partial derivatives of fi with respect to the elements of
zyx=y1x,y11x,…,y1 m1-1 x,y2x,…,yn mn-1 x.
[dfdy] = fjac(x, y, neq, m)

Input Parameters

1:     x – double scalar
x, the independent variable.
2:     yneq* – double array
yij contains yi j x, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 x=yix.
3:     neq – int64int32nag_int scalar
The number of differential equations.
4:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.

Output Parameters

1:     dfdyneqneq* – double array
dfdyijk+1 must contain the partial derivative of fi with respect to yj k , for i=1,2,…,neq, j=1,2,…,neq and k=0,1,…,mj-1. Only nonzero partial derivatives need be set.
3:     gafun – function handle or string containing name of m-file
gafun must evaluate the boundary conditions at the left-hand end of the range, that is functions gizya for given values of zya.
[ga] = gafun(ya, neq, m, nlbc)

Input Parameters

1:     yaneq* – double array
yaij contains yi j a, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 a=yia.
2:     neq – int64int32nag_int scalar
The number of differential equations.
3:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.
4:     nlbc – int64int32nag_int scalar
The number of boundary conditions at a.

Output Parameters

1:     ganlbc – double array
gai must contain gizya, for i=1,2,…,nlbc.
4:     gbfun – function handle or string containing name of m-file
gbfun must evaluate the boundary conditions at the right-hand end of the range, that is functions g-izyb for given values of zyb.
[gb] = gbfun(yb, neq, m, nrbc)

Input Parameters

1:     ybneq* – double array
ybij contains yi j b, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 b=yib.
2:     neq – int64int32nag_int scalar
The number of differential equations.
3:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.
4:     nrbc – int64int32nag_int scalar
The number of boundary conditions at b.

Output Parameters

1:     gbnrbc – double array
gbi must contain g-izyb, for i=1,2,…,nrbc.
5:     gajac – function handle or string containing name of m-file
gajac must evaluate the partial derivatives of gizya with respect to the elements of zya=y1a,y11a,…,y1 m1-1 a,y2a,…,yn mn-1 a.
[dgady] = gajac(ya, neq, m, nlbc)

Input Parameters

1:     yaneq* – double array
yaij contains yi j a, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 a=yia.
2:     neq – int64int32nag_int scalar
The number of differential equations.
3:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.
4:     nlbc – int64int32nag_int scalar
The number of boundary conditions at a.

Output Parameters

1:     dgadynlbcneq* – double array
dgadyijk+1 must contain the partial derivative of gizya with respect to yj k a, for i=1,2,…,nlbc, j=1,2,…,neq and k=0,1,…,mj-1. Only nonzero partial derivatives need be set.
6:     gbjac – function handle or string containing name of m-file
gbjac must evaluate the partial derivatives of g-izyb with respect to the elements of zyb=y1b,y11b,…,y1 m1-1 b,y2b,…,yn mn-1 b.
[dgbdy] = gbjac(yb, neq, m, nrbc)

Input Parameters

1:     ybneq* – double array
ybij contains yi j b, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 b=yib.
2:     neq – int64int32nag_int scalar
The number of differential equations.
3:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.
4:     nrbc – int64int32nag_int scalar
The number of boundary conditions at b.

Output Parameters

1:     dgbdynrbcneq* – double array
dgbdyijk must contain the partial derivative of g-izyb with respect to yj k b, for i=1,2,…,nrbc, j=1,2,…,neq and k=0,1,…,mj-1. Only nonzero partial derivatives need be set.
7:     guess – function handle or string containing name of m-file
guess must return initial approximations for the solution components yi j  and the derivatives yi mi , for i=1,2,…,neq and j=0,1,…,mi-1. Try to compute each derivative yi mi  such that it corresponds to your approximations to y i j , for j=0,1,…,mi-1. You should not call ffun to compute yi mi .
If nag_ode_bvp_coll_nlin (d02tk) is being used in conjunction with nag_ode_bvp_coll_nlin_contin (d02tx) as part of a continuation process, then guess is not called by nag_ode_bvp_coll_nlin (d02tk) after the call to nag_ode_bvp_coll_nlin_contin (d02tx).
[y, dym] = guess(x, neq, m)

Input Parameters

1:     x – double scalar
x, the independent variable; x∈a,b.
2:     neq – int64int32nag_int scalar
The number of differential equations.
3:     mneq – int64int32nag_int array
mi contains mi, the order of the ith differential equation, for i=1,2,…,neq.

Output Parameters

1:     yneq* – double array
yij must contain yi j x, for i=1,2,…,neq and j=0,1,…,mi-1.
Note:  yi 0 x=yix.
2:     dymneq – double array
dymi must contain yi mi x, for i=1,2,…,neq.
8:     rcomm* – double array
This must be the same array as supplied to nag_ode_bvp_coll_nlin_setup (d02tv) and must remain unchanged between calls.
9:     icomm* – int64int32nag_int array
This must be the same array as supplied to nag_ode_bvp_coll_nlin_setup (d02tv) and must remain unchanged between calls.

Optional Input Parameters

None.

Output Parameters

1:     rcomm* – double array
Contains information about the solution for use on subsequent calls to associated functions.
2:     icomm* – int64int32nag_int array
Contains information about the solution for use on subsequent calls to associated functions.
3:     ifail – int64int32nag_int scalar
ifail=0 unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Note: nag_ode_bvp_coll_nlin (d02tk) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:
   ifail=1
On entry, an invalid call was made to nag_ode_bvp_coll_nlin (d02tk), for example, without a previous call to the setup function nag_ode_bvp_coll_nlin_setup (d02tv).
   ifail=2
Numerical singularity has been detected in the Jacobian used in the underlying Newton iteration. No meaningful results have been computed. You should check carefully how you have coded fjac, gajac and gbjac. If the user-supplied functions have been coded correctly then supplying a different initial approximation to the solution in guess might be appropriate. See also Further Comments.
   ifail=3
The nonlinear iteration has failed to converge. At no time during the computation was convergence obtained and no meaningful results have been computed. You should check carefully how you have coded procedures fjac, gajac and gbjac. If the procedures have been coded correctly then supplying a better initial approximation to the solution in guess might be appropriate. See also Further Comments.
   ifail=4
The nonlinear iteration has failed to converge. At some earlier time during the computation convergence was obtained and the corresponding results have been returned for diagnostic purposes and may be inspected by a call to nag_ode_bvp_coll_nlin_diag (d02tz). Nothing can be said regarding the suitability of these results for use in any subsequent computation for the same problem. You should try to provide a better mesh and initial approximation to the solution in guess. See also Further Comments.
   ifail=5
The expected number of sub-intervals required exceeds the maximum number specified by the argument mxmesh in the setup function nag_ode_bvp_coll_nlin_setup (d02tv). Results for the last mesh on which convergence was obtained have been returned. Nothing can be said regarding the suitability of these results for use in any subsequent computation for the same problem. An indication of the error in the solution on the last mesh where convergence was obtained can be obtained by calling nag_ode_bvp_coll_nlin_diag (d02tz). The error requirements may need to be relaxed and/or the maximum number of mesh points may need to be increased. See also Further Comments.
   ifail=-99
An unexpected error has been triggered by this routine. Please contact NAG.
   ifail=-399
Your licence key may have expired or may not have been installed correctly.
   ifail=-999
Dynamic memory allocation failed.

Accuracy

The accuracy of the solution is determined by the argument tols in the prior call to nag_ode_bvp_coll_nlin_setup (d02tv) (see Description and Further Comments in nag_ode_bvp_coll_nlin_setup (d02tv) for details and advice). Note that error control is applied only to solution components (variables) and not to any derivatives of the solution. An estimate of the maximum error in the computed solution is available by calling nag_ode_bvp_coll_nlin_diag (d02tz).

Further Comments

If nag_ode_bvp_coll_nlin (d02tk) returns with ifail=2, 3, 4 or 5 and the call to nag_ode_bvp_coll_nlin (d02tk) was a part of some continuation procedure for which successful calls to nag_ode_bvp_coll_nlin (d02tk) have already been made, then it is possible that the adjustment(s) to the continuation argument(s) between calls to nag_ode_bvp_coll_nlin (d02tk) is (are) too large for the problem under consideration. More conservative adjustment(s) to the continuation argument(s) might be appropriate.

Example

The following example is used to illustrate the treatment of a high-order system, control of the error in a derivative of a component of the original system, and the use of continuation. See also nag_ode_bvp_coll_nlin_setup (d02tv), nag_ode_bvp_coll_nlin_contin (d02tx), nag_ode_bvp_coll_nlin_interp (d02ty) and nag_ode_bvp_coll_nlin_diag (d02tz), for the illustration of other facilities.
Consider the steady flow of an incompressible viscous fluid between two infinite coaxial rotating discs. See Ascher et al. (1979) and the references therein. The governing equations are
1R f′′′+ff′′′+gg′ = 0 1R g′′+fg′-f′g = 0  
subject to the boundary conditions
f0=f′0= 0,   g0=Ω0,   f1=f′1= 0,   g1=Ω1,  
where R is the Reynolds number and Ω0,Ω1 are the angular velocities of the disks.
We consider the case of counter-rotation and a symmetric solution, that is Ω0=1, Ω1=-1. This problem is more difficult to solve, the larger the value of R. For illustration, we use simple continuation to compute the solution for three different values of R (=106,108,1010). However, this problem can be addressed directly for the largest value of R considered here. Instead of the values suggested in Arguments in nag_ode_bvp_coll_nlin_contin (d02tx) for nmesh, ipmesh and mesh in the call to nag_ode_bvp_coll_nlin_contin (d02tx) prior to a continuation call, we use every point of the final mesh for the solution of the first value of R, that is we must modify the contents of ipmesh. For illustrative purposes we wish to control the computed error in f′ and so recast the equations as
y1′ = y2 y2′′′ = -Ry1y2′′+y3y3′ y3′′ = Ry2y3-y1y3′  
subject to the boundary conditions
y10=y20= 0,   y30=Ω,   y11=y21= 0,   y31=-Ω,   Ω=1.  
For the symmetric boundary conditions considered, there exists an odd solution about x=0.5. Hence, to satisfy the boundary conditions, we use the following initial approximations to the solution in guess:
y1x = -x2x-12 x-1 2 y2x = -xx-15⁢x2-5x+1 y3x = -8Ω x-12 3.  

Open in the MATLAB editor: d02tk_example

function d02tk_example


fprintf('d02tk example results\n\n');

global omega sqrofr; % For communication with local functions

% Initialize variables and arrays.
neq = 3;
nlbc = 3;
nrbc = 3;
ncol = 7;
mmax = 3;
m = [1; 3; 2];
tols = [1.0e-04; 1.0e-04; 1.0e-04];

% Set values for problem-specific physical parameters.
omega = 1.0;
r = 1.0e+6;

% Set up the mesh.
nmesh = 11;
mxmesh = 51;
ipmesh = zeros(mxmesh, 1);
mesh = zeros(mxmesh, 1);

% Set location of mesh boundaries, then calculate initial spacing.
mesh(1) = 0.0;
mesh(nmesh) = 1.0;
mstep = (mesh(nmesh) - mesh(1))/double(nmesh-1);
for i = 2:nmesh-1
  mesh(i) = mstep*double(i-1);
  ipmesh(i) = 2;
end

% Specify mesh end points as fixed.
ipmesh(1)     = 1;
ipmesh(nmesh) = 1;

% d02tv is a setup routine to be called prior to d02tk.
[work, iwork, ifail] = d02tv( ...
                              int64(m), int64(nlbc), int64(nrbc), ...
                              int64(ncol), tols, int64(nmesh), mesh, ...
                              int64(ipmesh));

% Set number of continuation steps.
ncont = 3;

% We run through the calculation three times with different parameter sets.
for jcont = 1:ncont
  sqrofr = sqrt(r);
  fprintf('\n Tolerance = %8.1e  R = %10.3e\n\n', tols(1), r);

  % Call d02tk to solve BVP for this set of parameters.
  [work, iwork, ifail] = d02tk( ...
                                @ffun, @fjac, @gafun, @gbfun, @gajac, ...
                                @gbjac, @guess, work, iwork);

  % Call d02tz to extract mesh from solution.
  [nmesh, mesh, ipmesh, ermx, iermx, ijermx, ifail] = ...
  d02tz( ...
         int64(mxmesh), work, iwork);

  % Output mesh results.
  fprintf(' Used a mesh of %d points\n', nmesh);
  fprintf([' Maximum error = %10.2e in interval %d for component %d\n\n', ...
           ' Mesh points:\n'], ermx, iermx, ijermx);
  for imesh = 1:nmesh
    fprintf( '%4d(%d) %6.4f', imesh, ipmesh(imesh), mesh(imesh));
    if mod(imesh, 4) == 0
      fprintf('\n');
    end
  end

  % Output solution, and store it for plotting.
  xarray = zeros(nmesh, 1);
  yarray = zeros(nmesh, 3);
  fprintf('\n\n    x        f         f''        g\n');
  for imesh = 1:nmesh
    % Call d02ty to perform interpolation on the solution.
    [y, work, ifail] = d02ty( ...
                              mesh(imesh), int64(neq), int64(mmax), ...
                              work, iwork);
    fprintf(' %6.3f  %8.4f  %8.4f  %8.4f\n', mesh(imesh), ...
            y(1,1), y(2,1), y(3,1));
    xarray(imesh) = mesh(imesh);
    yarray(imesh, 1:3) = y(1:3,1);
  end

  % Plot results for this parameter set.
  if jcont==1
    fig1 = figure;
  elseif jcont==2
    fig2 = figure;
  else
    fig3 = figure;
  end        
  display_plot(xarray, yarray, r)

  % Select mesh for next calculation.
  if jcont < ncont
    r = r*1.0e+02;
    for i = 2:nmesh-1
      ipmesh(i) = 2;
    end

    % d02tx allows the current solution to be used as an initial
    % approximation to the solution of a related problem.
    [work, iwork, ifail] = d02tx( ...
                                  nmesh, mesh, ipmesh, work, iwork);
  end
end



function [f] = ffun(x, y, neq, m)
  % Evaluate derivative functions (rhs of system of ODEs).

  global omega sqrofr; % For communication with main routine.
  f = zeros(neq, 1);
  f(1,1) =   y(2,1);
  f(2,1) = -(y(1,1)*y(2,3) + y(3,1)*y(3,2))*sqrofr;
  f(3,1) =  (y(2,1)*y(3,1) - y(1,1)*y(3,2))*sqrofr;

function [dfdy] = fjac(x, y, neq, m)
  % Evaluate Jacobians (partial derivatives of f).

  global omega sqrofr; % For communication with main routine.
  dfdy = zeros(neq, neq, 3);
  dfdy(1,2,1) =  1.0;
  dfdy(2,1,1) = -y(2,3)*sqrofr;
  dfdy(2,2,3) = -y(1,1)*sqrofr;
  dfdy(2,3,1) = -y(3,2)*sqrofr;
  dfdy(2,3,2) = -y(3,1)*sqrofr;
  dfdy(3,1,1) = -y(3,2)*sqrofr;
  dfdy(3,2,1) =  y(3,1)*sqrofr;
  dfdy(3,3,1) =  y(2,1)*sqrofr;
  dfdy(3,3,2) = -y(1,1)*sqrofr;

function [ga] = gafun(ya, neq, m, nlbc)
  % Evaluate boundary conditions at left-hand end of range.

  global omega sqrofr; % For communication with main routine.
  ga = zeros(nlbc, 1);
  ga(1) = ya(1);
  ga(2) = ya(2);
  ga(3) = ya(3) - omega;

function [dgady] = gajac(ya, neq, m, nlbc)
  % Evaluate Jacobians (partial derivatives of ga).

  dgady = zeros(nlbc, neq, 3);
  dgady(1,1,1) = 1.0;
  dgady(2,2,1) = 1.0;
  dgady(3,3,1) = 1.0;

function [gb] = gbfun(yb, neq, m, nrbc)
  % Evaluate boundary conditions at right-hand end of range.

  global omega sqrofr; % For communication with main routine.
  gb = zeros(nrbc, 1);
  gb(1) = yb(1);
  gb(2) = yb(2);
  gb(3) = yb(3) + omega;

  function [dgbdy] = gbjac(yb, neq, m, nrbc)
    % Evaluate Jacobians (partial derivatives of gb).

    dgbdy = zeros(nrbc, neq, 3);
    dgbdy(1,1,1) = 1.0;
    dgbdy(2,2,1) = 1.0;
    dgbdy(3,3,1) = 1.0;

function [y, dym] = guess(x, neq, m)
  % Evaluate initial approximations to solution components and derivatives.

  global omega sqrofr; % For communication with main routine.
  y = zeros(neq, 3);
  dym = zeros(neq, 1);
  y(1,1) = -x^2*(x - 0.5)*(x - 1.0)^2;
  y(2,1) = -x*(x - 1.0)*(5.0*x^2 - 5.0*x + 1.0);
  y(3,1) = -8.0*omega*(x - 0.5)^3;
  y(2,2) = -(20.0*x^3 - 30.0*x^2 + 12.0*x - 1.0);
  y(2,3) = -(60.0*x^2 - 60.0*x + 12.0*x);
  y(3,2) = -24.0*omega*(x - 0.5)^2;

  dym(1) = y(2,1);
  dym(2) = -(120.0*x - 60.0);
  dym(3) = -56.0*omega*(x - 0.5);

function display_plot(x, y, r)
  % Plot two of the curves, then add the other one.
  [haxes, hline1, hline2] = plotyy(x, y(:,2), x, y(:,3));
  % We want the third curve to be plotted on the left-hand y-axis.
  hold(haxes(1), 'on');
  hline3 = plot(x, y(:,1));
  % Set the axis limits and the tick specifications to beautify the plot.
  set(haxes(1), 'YLim', [-0.1 0.4]);
  set(haxes(1), 'XMinorTick', 'on', 'YMinorTick', 'on');
  set(haxes(1), 'YTick', [-0.1:0.1:0.4]);
  set(haxes(2), 'YLim', [-1 1]);
  set(haxes(2), 'YMinorTick', 'on');
  set(haxes(2), 'YTick', [-1:0.5:1]);
  for iaxis = 1:2
    % These properties must be the same for both sets of axes.
    set(haxes(iaxis), 'XLim', [0 1]);
    set(haxes(iaxis), 'XTick', [0:0.2:1]);
  end
  set(gca, 'box', 'off'); % no ticks on opposite axes.
  % Add title.
  ord = log10(r);
  title({'Incompressible Fluid Flow between Discs.', ...
         ['Solutions for Re = 10^n, n = ', num2str(ord)]});
  % Label the axes.
  xlabel('x');
  ylabel(haxes(1), 'f and f''');
  ylabel(haxes(2), 'g');
  % Add a legend.
  legend('f''','f','g','Location','Best')
  % Set some features of the three lines.
  set(hline1, 'Linewidth', 0.25, 'Marker', '+', 'LineStyle', '-', ...
      'Color', 'Magenta');
  set(hline2, 'Linewidth', 0.25, 'Marker', 'x', 'LineStyle', '--');
  set(hline3, 'Linewidth', 0.25, 'Marker', '*', 'LineStyle', ':');

d02tk example results


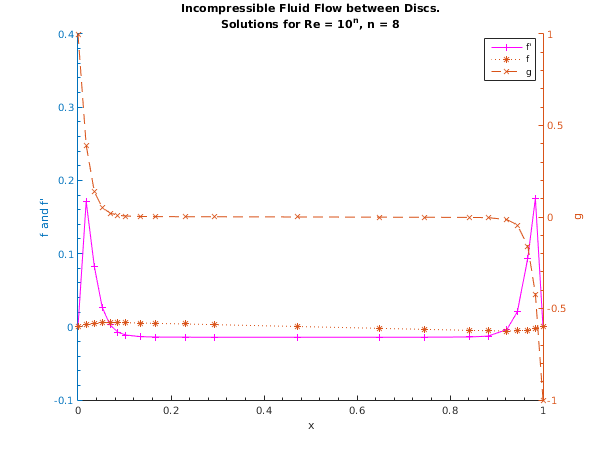
 Tolerance =  1.0e-04  R =  1.000e+06

 Used a mesh of 21 points
 Maximum error =   6.16e-10 in interval 20 for component 3

 Mesh points:
   1(1) 0.0000   2(3) 0.0500   3(2) 0.1000   4(3) 0.1500
   5(2) 0.2000   6(3) 0.2500   7(2) 0.3000   8(3) 0.3500
   9(2) 0.4000  10(3) 0.4500  11(2) 0.5000  12(3) 0.5500
  13(2) 0.6000  14(3) 0.6500  15(2) 0.7000  16(3) 0.7500
  17(2) 0.8000  18(3) 0.8500  19(2) 0.9000  20(3) 0.9500
  21(1) 1.0000

    x        f         f'        g
  0.000    0.0000    0.0000    1.0000
  0.050    0.0070    0.1805    0.4416
  0.100    0.0141    0.0977    0.1886
  0.150    0.0171    0.0252    0.0952
  0.200    0.0172   -0.0165    0.0595
  0.250    0.0157   -0.0400    0.0427
  0.300    0.0133   -0.0540    0.0322
  0.350    0.0104   -0.0628    0.0236
  0.400    0.0071   -0.0683    0.0156
  0.450    0.0036   -0.0714    0.0078
  0.500    0.0000   -0.0724    0.0000
  0.550   -0.0036   -0.0714   -0.0078
  0.600   -0.0071   -0.0683   -0.0156
  0.650   -0.0104   -0.0628   -0.0236
  0.700   -0.0133   -0.0540   -0.0322
  0.750   -0.0157   -0.0400   -0.0427
  0.800   -0.0172   -0.0165   -0.0595
  0.850   -0.0171    0.0252   -0.0952
  0.900   -0.0141    0.0977   -0.1886
  0.950   -0.0070    0.1805   -0.4416
  1.000   -0.0000    0.0000   -1.0000

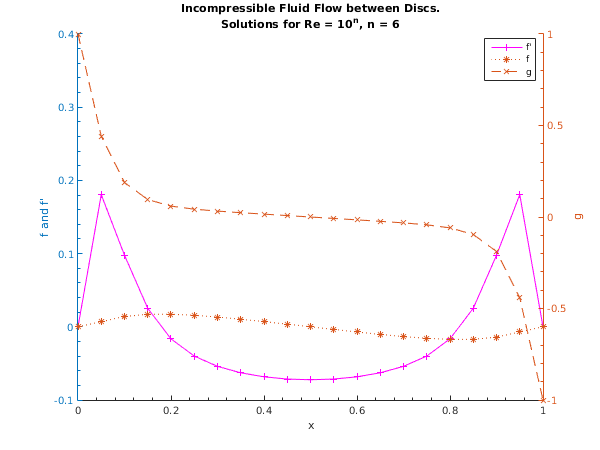
 Tolerance =  1.0e-04  R =  1.000e+08

 Used a mesh of 21 points
 Maximum error =   4.49e-09 in interval 6 for component 3

 Mesh points:
   1(1) 0.0000   2(3) 0.0176   3(2) 0.0351   4(3) 0.0520
   5(2) 0.0689   6(3) 0.0859   7(2) 0.1030   8(3) 0.1351
   9(2) 0.1672  10(3) 0.2306  11(2) 0.2939  12(3) 0.4713
  13(2) 0.6486  14(3) 0.7455  15(2) 0.8423  16(3) 0.8824
  17(2) 0.9225  18(3) 0.9449  19(2) 0.9673  20(3) 0.9836
  21(1) 1.0000

    x        f         f'        g
  0.000    0.0000    0.0000    1.0000
  0.018    0.0025    0.1713    0.3923
  0.035    0.0047    0.0824    0.1381
  0.052    0.0056    0.0267    0.0521
  0.069    0.0058    0.0025    0.0213
  0.086    0.0057   -0.0073    0.0097
  0.103    0.0056   -0.0113    0.0053
  0.135    0.0052   -0.0135    0.0027
  0.167    0.0047   -0.0140    0.0020
  0.231    0.0038   -0.0142    0.0015
  0.294    0.0029   -0.0142    0.0012
  0.471    0.0004   -0.0143    0.0002
  0.649   -0.0021   -0.0143   -0.0008
  0.745   -0.0035   -0.0142   -0.0014
  0.842   -0.0049   -0.0139   -0.0022
  0.882   -0.0054   -0.0127   -0.0036
  0.922   -0.0058   -0.0036   -0.0141
  0.945   -0.0057    0.0205   -0.0439
  0.967   -0.0045    0.0937   -0.1592
  0.984   -0.0023    0.1753   -0.4208
  1.000    0.0000    0.0000   -1.0000

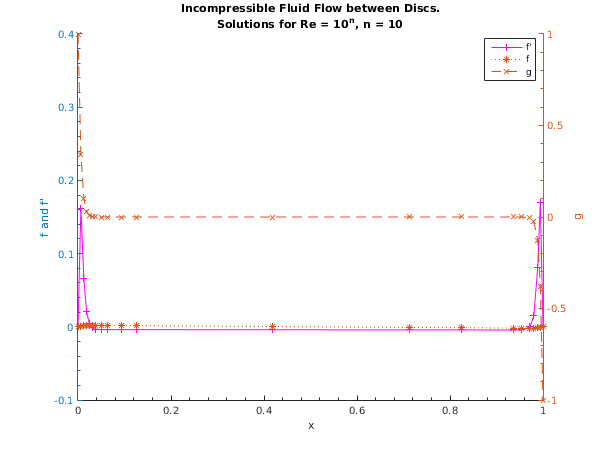
 Tolerance =  1.0e-04  R =  1.000e+10

 Used a mesh of 21 points
 Maximum error =   3.13e-06 in interval 7 for component 3

 Mesh points:
   1(1) 0.0000   2(3) 0.0063   3(2) 0.0125   4(3) 0.0185
   5(2) 0.0245   6(3) 0.0308   7(2) 0.0370   8(3) 0.0500
   9(2) 0.0629  10(3) 0.0942  11(2) 0.1256  12(3) 0.4190
  13(2) 0.7125  14(3) 0.8246  15(2) 0.9368  16(3) 0.9544
  17(2) 0.9719  18(3) 0.9803  19(2) 0.9886  20(3) 0.9943
  21(1) 1.0000

    x        f         f'        g
  0.000    0.0000    0.0000    1.0000
  0.006    0.0009    0.1623    0.3422
  0.013    0.0016    0.0665    0.1021
  0.019    0.0018    0.0204    0.0318
  0.025    0.0019    0.0041    0.0099
  0.031    0.0019   -0.0014    0.0028
  0.037    0.0019   -0.0031    0.0007
  0.050    0.0019   -0.0038   -0.0002
  0.063    0.0018   -0.0038   -0.0003
  0.094    0.0017   -0.0039   -0.0003
  0.126    0.0016   -0.0039   -0.0002
  0.419    0.0004   -0.0041   -0.0001
  0.712   -0.0008   -0.0042    0.0001
  0.825   -0.0013   -0.0043    0.0002
  0.937   -0.0018   -0.0043    0.0003
  0.954   -0.0019   -0.0042    0.0001
  0.972   -0.0019   -0.0003   -0.0049
  0.980   -0.0019    0.0152   -0.0252
  0.989   -0.0015    0.0809   -0.1279
  0.994   -0.0008    0.1699   -0.3814
  1.000   -0.0000   -0.0000   -1.0000
d02tk_fig1.png
d02tk_fig2.png
d02tk_fig3.png
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015