d02pz:: Ordinary Differential EquationsIntegrators for Stiff Ordinary Differential Systems (NAG Toolbox)

After a call to nag_ode_ivp_rk_range (d02pc) or nag_ode_ivp_rk_onestep (d02pd), nag_ode_ivp_rk_errass (d02pz) can be called for information about error assessment, if this assessment was specified in the setup function nag_ode_ivp_rk_setup (d02pv). A more accurate ‘true’ solution

\hat{y}

is computed in a secondary integration. The error is measured as specified in nag_ode_ivp_rk_setup (d02pv) for local error control. At each step in the primary integration, an average magnitude

μ_{i}

of component

y_{i}

is computed, and the error in the component is

\frac{|y_{i} - {\hat{y}}_{i}|}{\max (μ_{i}, thres (i))} .

It is difficult to estimate reliably the true error at a single point. For this reason the RMS (root-mean-square) average of the estimated global error in each solution component is computed. This average is taken over all steps from the beginning of the integration through to the current integration point. If all has gone well, the average errors reported will be comparable to tol (see nag_ode_ivp_rk_setup (d02pv)). The maximum error seen in any component in the integration so far and the point where the maximum error first occurred are also reported.

References

Parameters

Compulsory Input Parameters

Optional Input Parameters

Output Parameters

Error Indicators and Warnings

Accuracy

Further Comments

Example

This example integrates a two body problem. The equations for the coordinates

(x (t), y (t))

of one body as functions of time

t

in a suitable frame of reference are

x^{''} = - \frac{x}{r^{3}}, y^{''} = - \frac{y}{r^{3}}, r = \sqrt{x^{2} + y^{2}} .

The initial conditions

\begin{array}{l} x (0) = 1 - ε, & x^{'} (0) = 0 \\ y (0) = 0, & y^{'} (0) = \sqrt{\frac{1 + ε}{1 - ε}} \end{array}

lead to elliptic motion with

0 < ε < 1

ε = 0.7

is selected and reposed as

\begin{array}{l} y_{1}^{'} = y_{3} \\ y_{2}^{'} = y_{4} \\ y_{3}^{'} = - \frac{y_{1}}{r^{3}} \\ y_{4}^{'} = - \frac{y_{2}}{r^{3}} \end{array}

over the range

[0, 3 π]

. Relative error control is used with threshold values of

1.0e−10

for each solution component and a high-order Runge–Kutta method (

method = 3

) with tolerance

tol = 1.0e−6

. The value of

π

is obtained by using nag_math_pi (x01aa).

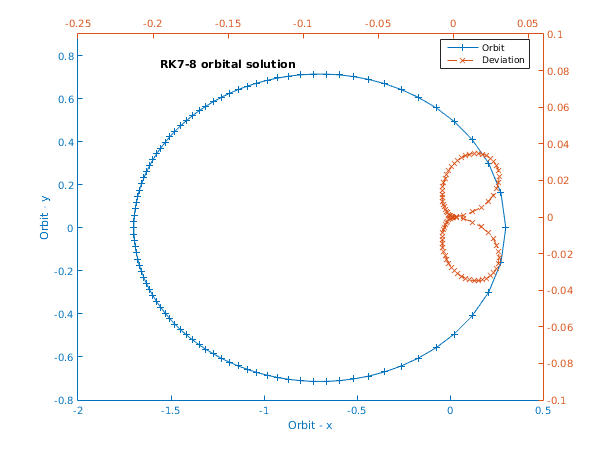
function d02pz_example


fprintf('d02pz example results\n\n');

% Initialize variables and arrays.
neq = int64(4);
lenwrk = int64(32*neq);
method = int64(3);
ecc = 0.7;

tstart = 0.0;
ystart = [1.0-ecc; 0.0; 0.0; sqrt((1.0+ecc)/(1.0-ecc))];
tend = 3.0*pi;
thres = [1e-10; 1e-10; 1e-10; 1e-10];
task = 'Usual Task';  % tell d02pv to use d02pc.
errass = true;
hstart = 0.0;
tol = 1.0e-6;

% We run through the calculation twice: once to output the results at
% a single point, and again to accumulate a series of results for plotting.
nstep = [1; 90];
tend = [3.0*pi; 2.0*pi];

% Prepare to accumulate results.  The first and last points should be the
% same - i.e. so the plot shows a closed trajectory.
xarray = zeros(nstep(2)+1, 1);
yarray = zeros(nstep(2)+1, 4);

for icalc = 1:2
  tinc  = tend(icalc)/nstep(icalc);

  if icalc == 1
    % Output initial results.
    fprintf('Calculation with tol = %1.1e\n\n',tol);
    fprintf('   t         y1        y2        y3        y4\n');
    fprintf(' %6.3f', tstart);
    fprintf('  %8.4f', ystart(1:neq));
    fprintf('\n');
  else
    xarray(1) = tstart;
    yarray(1, 1:neq) = ystart(1:neq);
  end

  for istep = 1:nstep(icalc)
    twant = istep*tinc;
    % d02pv is a setup routine to be called prior to d02pc.
    [work, ifail] = d02pv( ...
                           tstart, ystart, twant, tol, thres, method, ...
                           task, errass, lenwrk, 'neq', neq, 'hstart', hstart);
    
    % Initialize ygot and ymax.  These values don't matter for the
    % first call of d02pc, but they mustn't be changed in between
    % calls for the same problem.
    ygot = ystart;
    ymax = ystart;

    % In this demo, we disregard warnings about inefficiency from
    % d02pc (i.e. ifail = 2,3 or 4 - see documentation) and keep
    % calling the routine until the end of the range is reached.
    ifail = 2;
    while ifail >= 2 && ifail <= 4
      [tgot, ygot, ypgot, ymax, work, ifail] = ...
      d02pc( ...
             @f, neq, twant, ygot, ymax, work);
    end

    % Store the current result.
    if icalc == 2
      xarray(istep+1) = tgot;
      for ieq = 1:neq
        yarray(istep+1, ieq) = ygot(ieq);
      end
    end
  end

  % Output final results.
  if icalc == 1
    fprintf(' %6.3f', tgot);
    fprintf('  %8.4f', ygot(1:neq));
    fprintf('\n');
    
    % d02pz provides details about global error assessment computed
    % during integration with d02pc (or d02pd).
    [rmserr, errmax, terrmx, ifail] = ...
    d02pz(neq, work);
    fprintf('\nComponentwise error assessment:\n        ');
    fprintf(' %9.2e', rmserr(1:neq));
    fprintf('\n');
    fprintf(['\nWorst global error observed was %9.2e', ...
             ' - it occurred at T = %6.3f\n'], errmax, terrmx);

    % d02py is a diagnostic routine.
    [totfcn, stpcst, waste, stpsok, hnext, ifail] = ...
    d02py;
    fprintf(['\nCost of the integration in evaluations of ', ...
             'F is %1.0f\n\n\n'], totfcn);
  end
end

% Use the first two components of the solution, and calculate the deviation
% from a true ellipse.
x = yarray(:,1);
y = yarray(:,2);
xdev = zeros(nstep(2)+1, 1);
ydev = zeros(nstep(2)+1, 1);
for i = 1:nstep(2)+1
  fac = abs((x(i) + ecc)*(x(i) + ecc) + y(i)*y(i)/(ecc*ecc) - 1.0);
  xdev(i) = fac*cos(xarray(i));
  ydev(i) = fac*sin(xarray(i));
end

% Plot results.
fig1 = figure;
display_plot(x, y, xdev, ydev);


function [yp] = f(t, y, yp)
  % Evaluate derivative vector.

  yp = zeros(4, 1);
  r = sqrt((y(1)^2 + y(2)^2));
  yp(1) =  y(3);
  yp(2) =  y(4);
  yp(3) = -y(1)/r^3;
  yp(4) = -y(2)/r^3;

function display_plot(x1, y1, x2, y2)
  % Plot the results.  First, get the list of default colours (we have to
  % specify the plot colours by hand).
  axes('XLim', [-2 0.5], 'YLim', [-0.8 0.9]);
  cols = get(gca, 'ColorOrder');
  % Plot the first curve.
  hline1 = line(x1, y1, 'Color', cols(1,:));
  ax1 = gca;
  set(ax1, 'XColor', cols(1,:), 'YColor', cols(1,:));
  % Label these axes.
  xlabel('Orbit - x');
  ylabel('Orbit - y');
  % Set up the second set of axes and plot the second curve.
  ax2 = axes('Position', get(ax1,'Position'), ...
             'XAxisLocation', 'top', 'YAxisLocation', 'right', ...
             'Color','none', 'XColor',cols(2,:), 'YColor', cols(2,:), ...
             'XLim', [-0.25 0.06], 'YLim', [-0.1 0.1]);
  hline2 = line(x2, y2, 'Color', cols(2,:), 'Parent', ax2);
  % Label these axes.
  h = title('RK7-8 orbital solution');
  set(h,'Position',[-0.15,0.08]);
  % Add a legend, specifying the lines explicitly.
  legend([hline1, hline2],'Orbit','Deviation','Location','Best');
  % Set some features of the two lines.
  set(hline1, 'Linewidth', 0.25, 'Marker', '+', 'LineStyle', '-');
  set(hline2, 'Linewidth', 0.25, 'Marker', 'x', 'LineStyle', '--');

NAG Toolbox: nag_ode_withdraw_ivp_rk_errass (d02pz)

▸▿ Contents

Purpose

Syntax

Description