PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_ode_ivp_rkts_onestep (d02pf)
Purpose
nag_ode_ivp_rkts_onestep (d02pf) is a one-step function for solving an initial value problem for a first-order system of ordinary differential equations using Runge–Kutta methods.
Syntax
[
tnow,
ynow,
ypnow,
user,
iwsav,
rwsav,
ifail] = d02pf(
f,
n,
iwsav,
rwsav, 'user',
user)
[
tnow,
ynow,
ypnow,
user,
iwsav,
rwsav,
ifail] = nag_ode_ivp_rkts_onestep(
f,
n,
iwsav,
rwsav, 'user',
user)
Description
nag_ode_ivp_rkts_onestep (d02pf) and its associated functions
(
nag_ode_ivp_rkts_setup (d02pq),
nag_ode_ivp_rkts_reset_tend (d02pr),
nag_ode_ivp_rkts_interp (d02ps),
nag_ode_ivp_rkts_diag (d02pt) and
nag_ode_ivp_rkts_errass (d02pu)) solve an initial value problem for a first-order system of ordinary differential equations. The functions, based on Runge–Kutta methods and derived from RKSUITE (see
Brankin et al. (1991)), integrate
where
is the vector of
solution components and
is the independent variable.
nag_ode_ivp_rkts_onestep (d02pf) is designed to be used in complicated tasks when solving systems of ordinary differential equations. You must first call
nag_ode_ivp_rkts_setup (d02pq) to specify the problem and how it is to be solved. Thereafter you (repeatedly) call
nag_ode_ivp_rkts_onestep (d02pf) to take one integration step at a time from
tstart in the direction of
tend (as specified in
nag_ode_ivp_rkts_setup (d02pq)). In this manner
nag_ode_ivp_rkts_onestep (d02pf) returns an approximation to the solution
ynow and its derivative
ypnow at successive points
tnow. If
nag_ode_ivp_rkts_onestep (d02pf) encounters some difficulty in taking a step, the integration is not advanced and the function returns with the same values of
tnow,
ynow and
ypnow as returned on the previous successful step.
nag_ode_ivp_rkts_onestep (d02pf) tries to advance the integration as far as possible subject to passing the test on the local error and not going past
tend.
In the call to
nag_ode_ivp_rkts_setup (d02pq) you can specify either the first step size for
nag_ode_ivp_rkts_onestep (d02pf) to attempt or that it computes automatically an appropriate value. Thereafter
nag_ode_ivp_rkts_onestep (d02pf) estimates an appropriate step size for its next step. This value and other details of the integration can be obtained after any call to
nag_ode_ivp_rkts_onestep (d02pf) by a call to
nag_ode_ivp_rkts_diag (d02pt). The local error is controlled at every step as specified in
nag_ode_ivp_rkts_setup (d02pq). If you wish to assess the true error, you must set
method to a positive value
in the call to
nag_ode_ivp_rkts_setup (d02pq). This assessment can be obtained after any call to
nag_ode_ivp_rkts_onestep (d02pf) by a call to
nag_ode_ivp_rkts_errass (d02pu).
If you want answers at specific points there are two ways to proceed:
| (i) |
The more efficient way is to step past the point where a solution is desired, and then call nag_ode_ivp_rkts_interp (d02ps) to get an answer there. Within the span of the current step, you can get all the answers you want at very little cost by repeated calls to nag_ode_ivp_rkts_interp (d02ps). This is very valuable when you want to find where something happens, e.g., where a particular solution component vanishes. You cannot proceed in this way with
or .
|
| (ii) |
The other way to get an answer at a specific point is to set tend to this value and integrate to tend. nag_ode_ivp_rkts_onestep (d02pf) will not step past tend, so when a step would carry it past, it will reduce the step size so as to produce an answer at tend exactly. After getting an answer there (), you can reset tend to the next point where you want an answer, and repeat. tend could be reset by a call to nag_ode_ivp_rkts_setup (d02pq), but you should not do this. You should use nag_ode_ivp_rkts_reset_tend (d02pr) instead because it is both easier to use and much more efficient. This way of getting answers at specific points can be used with any of the available methods, but it is the only way with or . It can be inefficient. Should this be the case, the code will bring the matter to your attention. |
References
Brankin R W, Gladwell I and Shampine L F (1991) RKSUITE: A suite of Runge–Kutta codes for the initial value problems for ODEs SoftReport 91-S1 Southern Methodist University
Parameters
Compulsory Input Parameters
- 1:
– function handle or string containing name of m-file
-
f must evaluate the functions
(that is the first derivatives
) for given values of the arguments
,
.
[yp, user] = f(t, n, y, user)
Input Parameters
- 1:
– double scalar
-
, the current value of the independent variable.
- 2:
– int64int32nag_int scalar
-
, the number of ordinary differential equations in the system to be solved.
- 3:
– double array
-
The current values of the dependent variables,
, for .
- 4:
– Any MATLAB object
f is called from
nag_ode_ivp_rkts_onestep (d02pf) with the object supplied to
nag_ode_ivp_rkts_onestep (d02pf).
Output Parameters
- 1:
– double array
-
The values of
, for .
- 2:
– Any MATLAB object
- 2:
– int64int32nag_int scalar
-
, the number of ordinary differential equations in the system to be solved.
Constraint:
.
- 3:
– int64int32nag_int array
- 4:
– double array
-
These must be the same arrays supplied in a previous call to
nag_ode_ivp_rkts_setup (d02pq). They must remain unchanged between calls.
Optional Input Parameters
- 1:
– Any MATLAB object
user is not used by
nag_ode_ivp_rkts_onestep (d02pf), but is passed to
f. Note that for large objects it may be more efficient to use a global variable which is accessible from the m-files than to use
user.
Output Parameters
- 1:
– double scalar
-
, the value of the independent variable at which a solution has been computed.
- 2:
– double array
-
An approximation to the solution at
tnow. The local error of the step to
tnow was no greater than permitted by the specified tolerances (see
nag_ode_ivp_rkts_setup (d02pq)).
- 3:
– double array
-
An approximation to the first derivative of the solution at
tnow.
- 4:
– Any MATLAB object
- 5:
– int64int32nag_int array
- 6:
– double array
-
Information about the integration for use on subsequent calls to nag_ode_ivp_rkts_onestep (d02pf) or other associated functions.
- 7:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
A call to this function cannot be made after it has returned an error.
The setup function must be called to start another problem.
On entry, , but the value passed to the setup function was .
On entry, the communication arrays have become corrupted, or a catastrophic error has already been detected elsewhere. You cannot continue integrating the problem.
tend, as specified in the setup function, has already been reached.
To start a new problem, you will need to call the setup function.
To continue integration beyond
tend then
nag_ode_ivp_rkts_reset_tend (d02pr) must first be called to reset
tend to a new end value.
- W
-
More than
output points have been obtained by integrating to
tend (as specified in the setup function). They have been so clustered that it would probably be (much) more efficient to use the interpolation function
(if
,
switch to
at setup).
However, you can continue integrating the problem.
- W
-
Approximately function evaluations have been used to compute the solution since the integration started or since this message was last printed.
However, you can continue integrating the problem.
- W
-
Approximately
function evaluations have been used to compute the solution since the integration started or since this message was last printed. Your problem has been diagnosed as stiff. If the situation persists, it will cost roughly
times as much to reach
tend (setup) as it has cost to reach the current time. You should probably call functions intended for stiff problems. However, you can continue integrating the problem.
- W
-
In order to satisfy your error requirements the solver has to use a step size of
at the current time,
. This step size is too small for the
machine precision, and is smaller than
.
- W
-
The global error assessment algorithm failed at start of integration.
The integration is being terminated.
The global error assessment may not be reliable for times beyond .
The integration is being terminated.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
The accuracy of integration is determined by the arguments
tol and
thresh in a prior call to
nag_ode_ivp_rkts_setup (d02pq) (see the function document for
nag_ode_ivp_rkts_setup (d02pq) for further details and advice). Note that only the local error at each step is controlled by these arguments. The error estimates obtained are not strict bounds but are usually reliable over one step. Over a number of steps the overall error may accumulate in various ways, depending on the properties of the differential system.
Further Comments
If
nag_ode_ivp_rkts_onestep (d02pf) returns with
and the accuracy specified by
tol and
thresh is really required then you should consider whether there is a more fundamental difficulty. For example, the solution may contain a singularity. In such a region the solution components will usually be large in magnitude. Successive output values of
ynow should be monitored with the aim of trapping the solution before the singularity. In any case numerical integration cannot be continued through a singularity, and analytical treatment may be necessary.
Performance statistics are available after any return from
nag_ode_ivp_rkts_onestep (d02pf) (except when
) by a call to
nag_ode_ivp_rkts_diag (d02pt). If
in the call to
nag_ode_ivp_rkts_setup (d02pq), global error assessment is available after any return from
nag_ode_ivp_rkts_onestep (d02pf) (except when
) by a call to
nag_ode_ivp_rkts_errass (d02pu).
After a failure with
or
each of the diagnostic functions
nag_ode_ivp_rkts_diag (d02pt) and
nag_ode_ivp_rkts_errass (d02pu)
may be called only once.
If nag_ode_ivp_rkts_onestep (d02pf) returns with then it is advisable to change to another code more suited to the solution of stiff problems. nag_ode_ivp_rkts_onestep (d02pf) will not return with if the problem is actually stiff but it is estimated that integration can be completed using less function evaluations than already computed.
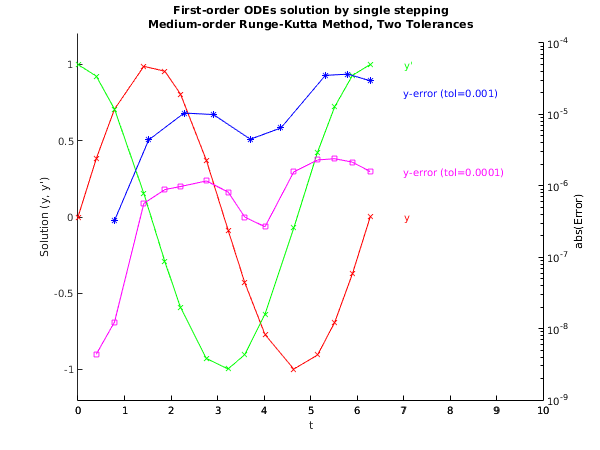
Example
This example solves the equation
reposed as
over the range
with initial conditions
and
. We use relative error control with threshold values of
for each solution component and print the solution at each integration step across the range. We use a medium order Runge–Kutta method
(
) with tolerances
and
in turn so that we may compare the solutions.
Open in the MATLAB editor:
d02pf_example
function d02pf_example
fprintf('d02pf example results\n\n');
method = int64(2);
tstart = 0;
tend = 2*pi;
yinit = [0;1];
hstart = 0;
thresh = [1e-08; 1e-08];
n = int64(2);
tol0 = 1.0E-4;
ynow = zeros(20, n);
tnow = zeros(20, 1);
err1 = zeros(20, 2);
err2 = zeros(20, 2);
tol = 10.0*tol0;
for i = 1:2
tol = tol*0.1;
[iwsav, rwsav, ifail] = d02pq(tstart, tend, yinit, tol, thresh, method);
tnow(1) = tstart;
ynow(1,:) = yinit;
j=1;
while tnow(j) < tend
j=j+1;
[tnow(j), ynow(j, :), ypnow, user, iwsav, rwsav, ifail] = ...
d02pf(@f, n, iwsav, rwsav);
err1(j, i) = ynow(j, 1)-sin(tnow(j));
err2(j, i) = ynow(j, 2)-cos(tnow(j));
end
fprintf('\nCalculation with TOL = %8.1e:\n\n', tol);
[fevals, stepcost, waste, stepsok, hnext, iwsav, ifail] = d02pt(iwsav, rwsav);
fprintf(' Number of evaluations of f = %d\n', fevals);
if i == 1
tnow1 = tnow;
end
npts(i) = j;
end
fig1 = figure;
title({['First-order ODEs solution by single stepping'],...
['Medium-order Runge-Kutta Method, Two Tolerances']});
hold on;
axis([0 10 -1.2 1.2]);
xlabel('t');
ylabel('Solution (y, y'')');
plot(tnow(1:npts(2)), ynow(1:npts(2), 1), '-xr');
text(ceil(tnow(npts(2))), ynow(npts(2), 1), 'y', 'Color', 'r');
plot(tnow(1:npts(2)), ynow(1:npts(2), 2), '-xg');
text(ceil(tnow(npts(2))), ynow(npts(2), 2), 'y''', 'Color', 'g');
ax1 = gca;
ax2 = axes('Position',get(ax1,'Position'),...
'XAxisLocation','bottom','YAxisLocation','right',...
'YScale','log','Color','none','XColor','k','YColor','k');
hold on;
axis([0 10 1e-9 1e-4]);
ylabel('abs(Error)');
plot(ax2, tnow1(1:npts(1)), abs(err1(1:npts(1), 1)), '-*b');
text(ceil(tnow1(npts(1))), err1(npts(1), 1) - 1e-5, ...
'y-error (tol=0.001)', 'Color', 'b');
plot(ax2, tnow, abs(err1(:, 2)), '-sm');
text(ceil(tnow(npts(2))), err1(npts(2), 2), 'y-error (tol=0.0001)', ...
'Color', 'm');
hold off;
function [yp, user] = f(t, n, y, user)
yp = [y(2); -y(1)];
d02pf example results
Calculation with TOL = 1.0e-04:
Number of evaluations of f = 204
Calculation with TOL = 1.0e-05:
Number of evaluations of f = 314
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015