PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_ode_sl2_breaks_funs (d02ke)
Purpose
nag_ode_sl2_breaks_funs (d02ke) finds a specified eigenvalue of a regular or singular second-order Sturm–Liouville system on a finite or infinite interval, using a Pruefer transformation and a shooting method. It also reports values of the eigenfunction and its derivatives. Provision is made for discontinuities in the coefficient functions or their derivatives.
Syntax
[
match,
elam,
delam,
hmax,
maxit,
ifail] = d02ke(
xpoint,
match,
coeffn,
bdyval,
k,
tol,
elam,
delam,
hmax,
monit,
report, 'm',
m, 'maxit',
maxit, 'maxfun',
maxfun)
[
match,
elam,
delam,
hmax,
maxit,
ifail] = nag_ode_sl2_breaks_funs(
xpoint,
match,
coeffn,
bdyval,
k,
tol,
elam,
delam,
hmax,
monit,
report, 'm',
m, 'maxit',
maxit, 'maxfun',
maxfun)
Description
nag_ode_sl2_breaks_funs (d02ke) has essentially the same purpose as
nag_ode_sl2_breaks_vals (d02kd) with minor modifications to enable values of the eigenfunction to be obtained after convergence to the eigenvalue has been achieved.
It first finds a specified eigenvalue
of a Sturm–Liouville system defined by a self-adjoint differential equation of the second-order
together with appropriate boundary conditions at the two, finite or infinite, end points
and
. The functions
and
, which are real-valued, are defined by
coeffn. The boundary conditions must be defined by
bdyval, and, in the case of a singularity at
or
, take the form of an asymptotic formula for the solution near the relevant end point.
When the final estimate
of the eigenvalue has been found, the function integrates the differential equation once more with that value of
, and with initial conditions chosen so that the integral
is approximately one. When
is of the form
, which is the most common case,
represents the square of the norm of
induced by the inner product
with respect to which the eigenfunctions are mutually orthogonal. This normalization of
is only approximate, but experience shows that
generally differs from unity by only one or two per cent.
During this final integration the
report is called at each integration mesh point
. Sufficient information is returned to permit you to compute
and
for printing or plotting. For reasons described in
General Description of the Algorithm,
nag_ode_sl2_breaks_funs (d02ke) passes across to
report, not
and
, but the Pruefer variables
,
and
on which the numerical method is based. Their relationship to
and
is given by the equations
A specimen
report is given in
Example below.
For the theoretical basis of the numerical method to be valid, the following conditions should hold on the coefficient functions:
| (a) |
must be nonzero and must not change sign throughout the interval ; and, |
| (b) |
must not change sign throughout the interval for all relevant values of , and must not be identically zero as varies, for any . |
Points of discontinuity in the functions
and
or their derivatives are allowed, and should be included as ‘break-points’ in the array
xpoint.
A good account of the theory of Sturm–Liouville systems, with some description of Pruefer transformations, is given in Chapter X of
Birkhoff and Rota (1962). An introduction to the use of Pruefer transformations for the numerical solution of eigenvalue problems arising from physics and chemistry is given in
Bailey (1966).
The scaled Pruefer method is described in a short note by
Pryce and Hargrave (1977) and in some detail in the technical report by
Pryce (1981).
References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Bailey P B (1966) Sturm–Liouville eigenvalues via a phase function SIAM J. Appl. Math. 14 242–249
Banks D O and Kurowski I (1968) Computation of eigenvalues of singular Sturm–Liouville Systems Math. Comput. 22 304–310
Birkhoff G and Rota G C (1962) Ordinary Differential Equations Ginn & Co., Boston and New York
Pryce J D (1981) Two codes for Sturm–Liouville problems Technical Report CS-81-01 Department of Computer Science, Bristol University
Pryce J D and Hargrave B A (1977) The scaled Prüfer method for one-parameter and multi-parameter eigenvalue problems in ODEs IMA Numerical Analysis Newsletter 1(3)
Parameters
Compulsory Input Parameters
- 1:
– double array
-
The points where the boundary conditions computed by
bdyval are to be imposed, and also any break-points, i.e.,
to
must contain values
such that
with the following meanings:
| (a) |
and are the left- and right-hand end points, and , of the domain of definition of the Sturm–Liouville system if these are finite. If either or is infinite, the corresponding value or may be a more-or-less arbitrarily ‘large’ number of appropriate sign. |
| (b) |
and are the Boundary Matching Points (BMPs), that is the points at which the left and right boundary conditions computed in bdyval are imposed.
If the left-hand end point is a regular point then you should set , while if it is a singular point you must set . Similarly () if the right-hand end point is regular, and if it is singular. |
| (c) |
The remaining points , if any, define ‘break-points’ which divide the interval into sub-intervals
Numerical integration of the differential equation is stopped and restarted at each break-point. In simple cases no break-points are needed. However, if or are given by different formulae in different parts of the interval, then integration is more efficient if the range is broken up by break-points in the appropriate way. Similarly points where any jumps occur in or , or in their derivatives up to the fifth-order, should appear as break-points.
Examples are given in Further Comments and Example. xpoint determines the position of the Shooting Matching Point (SMP), as explained in The Position of the Shooting Matching Point . |
Constraint:
.
- 2:
– int64int32nag_int scalar
-
Must be set to the index of the ‘break-point’ to be used as the matching point (see
The Position of the Shooting Matching Point ). If
match is set to a value outside the range
then a default value is taken, corresponding to the break-point nearest the centre of the interval
.
- 3:
– function handle or string containing name of m-file
-
coeffn must compute the values of the coefficient functions
and
for given values of
and
.
Description states the conditions which
and
must satisfy. See
Examples of Coding the coeffn and
Example for examples.
[p, q, dqdl] = coeffn(x, elam, jint)
Input Parameters
- 1:
– double scalar
-
The current value of .
- 2:
– double scalar
-
The current trial value of the eigenvalue argument .
- 3:
– int64int32nag_int scalar
-
The index
of the sub-interval
(see specification of
xpoint) in which
lies.
Output Parameters
- 1:
– double scalar
-
The value of for the current value of .
- 2:
– double scalar
-
The value of for the current value of and the current trial value of .
- 3:
– double scalar
-
The value of
for the current value of
and the current trial value of
. However
dqdl is only used in error estimation and, in the rare cases where it may be difficult to evaluate, an approximation (say to within
) will suffice.
- 4:
– function handle or string containing name of m-file
-
bdyval must define the boundary conditions. For each end point,
bdyval must return (in
yl or
yr) values of
and
which are consistent with the boundary conditions at the end points; only the ratio of the values matters. Here
is a given point (
xl or
xr) equal to, or close to, the end point.
For a
regular end point (
, say),
, a boundary condition of the form
can be handled by returning constant values in
yl, e.g.,
and
.
For a
singular end point however,
and
will in general be functions of
xl and
elam, and
and
functions of
xr and
elam, usually derived analytically from a power-series or asymptotic expansion. Examples are given in
Examples of Boundary Conditions at Singular Points and
Example.
[yl, yr] = bdyval(xl, xr, elam)
Input Parameters
- 1:
– double scalar
-
If
is a regular end point of the system (so that
), then
xl contains
. If
is a singular point (so that
), then
xl contains a point
such that
.
- 2:
– double scalar
-
If
is a regular end point of the system (so that
), then
xr contains
. If
is a singular point (so that
), then
xr contains a point
such that
.
- 3:
– double scalar
-
The current trial value of .
Output Parameters
- 1:
– double array
-
and should contain values of and respectively (not both zero) which are consistent with the boundary condition at the left-hand end point, given by . should not be set.
- 2:
– double array
-
and should contain values of and respectively (not both zero) which are consistent with the boundary condition at the right-hand end point, given by . should not be set.
- 5:
– int64int32nag_int scalar
-
, the index of the required eigenvalue when the eigenvalues are ordered
Constraint:
.
- 6:
– double scalar
-
The tolerance argument which determines the accuracy of the computed eigenvalue. The error estimate held in
delam on exit satisfies the mixed absolute/relative error test
where
elam is the final estimate of the eigenvalue.
delam is usually somewhat smaller than the right-hand side of
(1) but not several orders of magnitude smaller.
Constraint:
.
- 7:
– double scalar
-
An initial estimate of the eigenvalue .
- 8:
– double scalar
-
An indication of the scale of the problem in the
-direction.
delam holds the initial ‘search step’ (positive or negative). Its value is not critical, but the first two trial evaluations are made at
elam and
, so the function will work most efficiently if the eigenvalue lies between these values. A reasonable choice (if a closer bound is not known) is half the distance between adjacent eigenvalues in the neighbourhood of the one sought. In practice, there will often be a problem, similar to the one in hand but with known eigenvalues, which will help one to choose initial values for
elam and
delam.
If on entry, it is given the default value of .
- 9:
– double array
-
should contain a maximum step size to be used by the differential equation code in the
th sub-interval
(as described in the specification of argument
xpoint), for
. If it is zero the function generates a maximum step size internally.
It is recommended that
be set to zero unless the coefficient functions
and
have features (such as a narrow peak) within the
th sub-interval that could be ‘missed’ if a long step were taken. In such a case
should be set to about half the distance over which the feature should be observed. Too small a value will increase the computing time for the function. See
Further Comments for further suggestions.
The rest of the array is used as workspace.
- 10:
– function handle or string containing name of m-file
-
monit is called by
nag_ode_sl2_breaks_funs (d02ke) at the end of each root-finding iteration and allows you to monitor the course of the computation by printing out the arguments (see
Example for an example).
If no monitoring is required, the dummy (sub)program nag_ode_sl2_reg_finite_dummy_monit (d02kay) may be used. (nag_ode_sl2_reg_finite_dummy_monit (d02kay) is included in the NAG Toolbox.)
monit(nit, iflag, elam, finfo)
Input Parameters
- 1:
– int64int32nag_int scalar
-
The current value of the argument
maxit of
nag_ode_sl2_breaks_funs (d02ke), this is decreased by one at each iteration.
- 2:
– int64int32nag_int scalar
-
Describes what phase the computation is in.
- An error occurred in the computation at this iteration; an error exit from nag_ode_sl2_breaks_funs (d02ke) with will follow.
- The function is trying to bracket the eigenvalue .
- The function is converging to the eigenvalue (having already bracketed it).
- 3:
– double scalar
-
The current trial value of .
- 4:
– double array
-
Information about the behaviour of the shooting method, and diagnostic information in the case of errors. It should not normally be printed in full if no error has occurred (that is, if
), though the first few components may be of interest to you. In case of an error (
) all the components of
finfo should be printed.
The contents of
finfo are as follows:
- The current value of the ‘miss-distance’ or ‘residual’ function on which the shooting method is based. (See General Description of the Algorithm for further information.) is set to zero if .
- An estimate of the quantity defined as follows. Consider the perturbation in the miss-distance that would result if the local error in the solution of the differential equation were always positive and equal to its maximum permitted value. Then is the perturbation in that would have the same effect on . Thus, at the zero of is an approximate bound on the perturbation of the zero (that is the eigenvalue) caused by errors in numerical solution. If is very large then it is possible that there has been a programming error in coeffn such that is independent of . If this is the case, an error exit with should follow. is set to zero if .
- The number of internal iterations, using the same value of and tighter accuracy tolerances, needed to bring the accuracy (that is, the value of ) to an acceptable value. Its value should normally be , and should almost never exceed .
- The number of calls to coeffn at this iteration.
- The number of successful steps taken by the internal differential equation solver at this iteration. A step is successful if it is used to advance the integration.
- The number of unsuccessful steps used by the internal integrator at this iteration.
- The number of successful steps at the maximum step size taken by the internal integrator at this iteration.
- Not used.
- to
- Set to zero, unless in which case they hold the following values describing the point of failure:
- The index of the sub-interval where failure occurred, in the range to . In case of an error in bdyval, it is set to or depending on whether the left or right boundary condition caused the error.
- The value of the independent variable, , the point at which the error occurred. In case of an error in bdyval, it is set to the value of xl or xr as appropriate (see the specification of bdyval).
- , ,
- The current values of the Pruefer dependent variables , and respectively. These are set to zero in case of an error in bdyval.
- The local-error tolerance being used by the internal integrator at the point of failure. This is set to zero in the case of an error in bdyval.
- The last integration mesh point. This is set to zero in the case of an error in bdyval.
- 11:
– function handle or string containing name of m-file
-
report provides the means by which you may compute the eigenfunction
and its derivative at each integration mesh point
. (See
Further Comments for an example.)
report(x, v, jint)
Input Parameters
- 1:
– double scalar
-
The current value of the independent variable
. See
The Position of the Shooting Matching Point for the order in which values of
are supplied.
- 2:
– double array
-
, , hold the current values of the Pruefer variables , , respectively.
- 3:
– int64int32nag_int scalar
-
Indicates the sub-interval between break-points in which
x lies exactly as for
coeffn,
except that at the extreme left-hand end point (when
)
jint is set to
and at the extreme right-hand end point (when
)
jint is set to
.
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
xpoint,
hmax. (An error is raised if these dimensions are not equal.)
The number of points in the array
xpoint.
Constraint:
.
- 2:
– int64int32nag_int scalar
Default:
A bound on
, the number of root-finding iterations allowed, that is the number of trial values of
that are used. If
, no such bound is assumed. (See also
maxfun.)
- 3:
– int64int32nag_int scalar
Suggested value:
.
maxfun and
maxit may be used to limit the computational cost of a call to
nag_ode_sl2_breaks_funs (d02ke), which is roughly proportional to
.
Default:
A bound on
, the number of calls to
coeffn made in any one root-finding iteration. If
, no such bound is assumed.
Output Parameters
- 1:
– int64int32nag_int scalar
-
The index of the break-point actually used as the matching point.
- 2:
– double scalar
-
The final computed estimate, whether or not an error occurred.
- 3:
– double scalar
-
If
,
delam holds an estimate of the absolute error in the computed eigenvalue, that is
. (In
General Description of the Algorithm we discuss the assumptions under which this is true.) The true error is rarely more than twice, or less than a tenth, of the estimated error.
If
,
delam may hold an estimate of the error, or its initial value, depending on the value of
ifail. See
Error Indicators and Warnings for further details.
- 4:
– double array
-
and
contain the sensitivity coefficients
, described in
The Sensitivity Parameters and . Other entries contain diagnostic output in the case of an error exit (see
Error Indicators and Warnings).
- 5:
– int64int32nag_int scalar
Default:
Will have been decreased by the number of iterations actually performed, whether or not it was positive on entry.
- 6:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
-
-
A argument error. All arguments (except
ifail) are left unchanged. The reason for the error is shown by the value of
as follows:
| : |
; |
| : |
; |
| : |
; |
| : |
to are not in ascending order. gives the position in xpoint where this was detected. |
-
-
At some call to
bdyval, invalid values were returned, that is, either
, or
(a programming error in
bdyval). See the last call of
monit for details.
This error exit will also occur if
is zero at the point where the boundary condition is imposed. Probably
bdyval was called with
xl equal to a singular end point
or with
xr equal to a singular end point
.
-
-
At some point between
xl and
xr the value of
computed by
coeffn became zero or changed sign. See the last call of
monit for details.
-
-
on entry, and after
maxit iterations the eigenvalue had not been found to the required accuracy.
-
-
The ‘bracketing’ phase (with argument
iflag of the
monit equal to
) failed to bracket the eigenvalue within ten iterations. This is caused by an error in formulating the problem (for example,
is independent of
), or by very poor initial estimates of
elam and
delam.
On exit,
elam and
give the end points of the interval within which no eigenvalue was located by the function.
-
-
on entry, and the last iteration was terminated because more than
maxfun calls to
coeffn were used. See the last call of
monit for details.
-
-
To obtain the desired accuracy the local error tolerance was set so small at the start of some sub-interval that the differential equation solver could not choose an initial step size large enough to make significant progress. See the last call of
monit for diagnostics.
-
-
At some point inside a sub-interval the step size in the differential equation solver was reduced to a value too small to make significant progress (for the same reasons as with
). This could be due to pathological behaviour of
and
or to an unreasonable accuracy requirement or to the current value of
making the equations ‘stiff’. See the last call of
monit for details.
- W
-
tol is too small for the problem being solved and the
machine precision is being used. The final value of
elam should be a very good approximation to the eigenvalue.
-
-
nag_roots_contfn_brent_rcomm (c05az), called by
nag_ode_sl2_breaks_funs (d02ke), has terminated with the error exit corresponding to a pole of the residual function
. This error exit should not occur, but if it does, try solving the problem again with a smaller value for
tol.
-
-
-
A serious error has occurred in an internal call. Check all (sub)program calls and array dimensions. Seek expert help.
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Note: error exits with
,
,
,
,
or
are caused by being unable to set up or solve the differential equation at some iteration and will be immediately preceded by a call of
monit giving diagnostic information. For other errors, diagnostic information is contained in
, for
, where appropriate.
Accuracy
Further Comments
Timing
The time taken by
nag_ode_sl2_breaks_funs (d02ke) depends on the complexity of the coefficient functions, whether they or their derivatives are rapidly changing, the tolerance demanded, and how many iterations are needed to obtain convergence. The amount of work per iteration is roughly doubled when
tol is divided by
. To make the most economical use of the function, one should try to obtain good initial values for
elam and
delam, and, where appropriate, good asymptotic formulae. Also the boundary matching points should not be set unnecessarily close to singular points. The extra time needed to compute the eigenfunction is principally the cost of one additional integration once the eigenvalue has been found.
General Description of the Algorithm
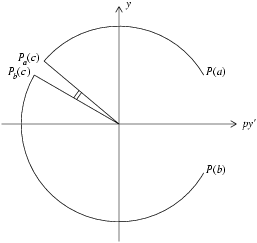
A shooting method, for differential equation problems containing unknown parameters, relies on the construction of a ‘miss-distance function’, which for given trial values of the parameters measures how far the conditions of the problem are from being met. The problem is then reduced to one of finding the values of the parameters for which the miss-distance function is zero, that is to a root-finding process. Shooting methods differ mainly in how the miss-distance is defined.
nag_ode_sl2_breaks_funs (d02ke) defines a miss-distance
based on the rotation about the origin of the point
in the Phase Plane as the solution proceeds from
to
. The
boundary conditions define the ray (i.e., two-sided line through the origin) on which
should start, and the ray on which it should finish. The
eigenvalue defines the total number of half-turns it should make. Numerical solution is actually done by ‘shooting forward’ from
and ‘shooting backward’ from
to a matching point
. Then
is taken as the angle between the rays to the two resulting points
and
. A relative scaling of the
and
axes, based on the behaviour of the coefficient functions
and
, is used to improve the numerical behaviour.
Figure 1
The resulting function is monotonic over , increasing if and decreasing if , with a unique zero at the desired eigenvalue . The function measures in units of a half-turn. This means that as increases, varies by about as each eigenvalue is passed. (This feature implies that the values of at successive iterations – especially in the early stages of the iterative process – can be used with suitable extrapolation or interpolation to help the choice of initial estimates for eigenvalues near to the one currently being found.)
The function actually computes a value for
with errors, arising from the local errors of the differential equation code and from the asymptotic formulae provided by you if singular points are involved. However, the error estimate output in
delam is usually fairly realistic, in that the actual error
is within an order of magnitude of
delam.
We pass the values of
,
,
across through
report rather than converting them to values of
,
inside
nag_ode_sl2_breaks_funs (d02ke), for the following reasons. First, there may be cases where auxiliary quantities can be more accurately computed from the Pruefer variables than from
and
. Second, in singular problems on an infinite interval
and
may underflow towards the end of the range, whereas the Pruefer variables remain well-behaved. Third, with high-order eigenvalues (and therefore highly oscillatory eigenfunctions) the eigenfunction may have a complete oscillation (or more than one oscillation) between two mesh points, so that values of
and
at mesh points give a very poor representation of the curve. The probable behaviour of the Pruefer variables in this case is that
and
vary slowly whilst
increases quickly: for all three Pruefer variables linear interpolation between the values at adjacent mesh points is probably sufficiently accurate to yield acceptable intermediate values of
,
,
(and hence of
) for graphical purposes.
Similar considerations apply to the exponentially decaying ‘tails’ of the eigenfunctions that often occur in singular problems. Here has approximately constant value whilst increases rapidly in the direction of integration, though the step length is generally fairly small over such a range.
If the solution is output through
report at
values which are too widely spaced, the step length can be controlled by choosing
hmax suitably, or, preferably, by reducing
tol. Both these choices will lead to more accurate eigenvalues and eigenfunctions but at some computational cost.
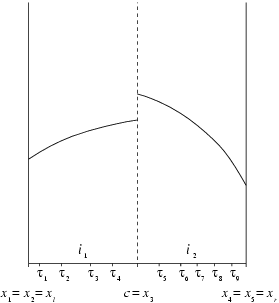
The Position of the Shooting Matching Point c
This point is always one of the values
in array
xpoint. It may be specified using the argument
match. The default value is chosen to be the value of that
,
, that lies closest to the middle of the interval
. If there is a tie, the rightmost candidate is chosen. In particular if there are no break-points, then
(
); that is, the shooting is from left to right in this case. A break-point may be inserted purely to move
to an interior point of the interval, even though the form of the equations does not require it. This often speeds up convergence especially with singular problems.
Note that the shooting method used by the code integrates first from the left-hand end
, then from the right-hand end
, to meet at the matching point
in the middle. This will of course be reflected in printed or graphical output. The diagram shows a possible sequence of nine mesh points
through
in the order in which they appear, assuming there are just two sub-intervals (so
).
Figure 2
Since the shooting method usually fails to match up the two ‘legs’ of the curve exactly, there is bound to be a jump in
, or in
or both, at the matching point
. The code in fact ‘shares’ the discrepancy out so that both
and
have a jump. A large jump does
not imply an inaccurate eigenvalue, but implies either
| (a) |
a badly chosen matching point: if has a ‘humped’ shape, should be chosen near the maximum value of , especially if is negative at the ends of the interval; |
| (b) |
an inherently ill-conditioned problem, typically one where another eigenvalue is pathologically close to the one being sought. In this case it is extremely difficult to obtain an accurate eigenfunction. |
In
Example, we find the 11th eigenvalue and corresponding eigenfunction of the equation
the boundary conditions being that
should remain bounded as
tends to
and
tends to
. The coding of this problem is discussed in detail in
Examples of Boundary Conditions at Singular Points.
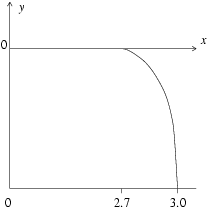
The choice of matching point
is open. If we choose
as in
nag_ode_sl2_breaks_vals (d02kd) example program we find that the exponentially increasing component of the solution dominates and we get extremely inaccurate values for the eigenfunction (though the eigenvalue is determined accurately). The values of the eigenfunction calculated with
are given schematically in
Figure 3.
Figure 3
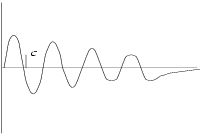
If we choose
as the maximum of the hump in
(see item
(a) above) we instead obtain the accurate results given in
Figure 4
Figure 4
Examples of Coding the coeffn
Coding
coeffn is straightforward except when break-points are needed. The examples below show:
| (a) |
a simple case, |
| (b) |
a case in which discontinuities in the coefficient functions or their derivatives necessitate break-points, and |
| (c) |
a case where break-points together with the hmax argument are an efficient way to deal with a coefficient function that is well-behaved except over one short interval. |
(Some of these cases are among the examples in
Example.)
Example A
The modified Bessel equation
Assuming the interval of solution does not contain the origin and dividing through by
, we have
and
. The code could be
function [p, q, dqdl] = coeffn(x, elam, jint)
global nu;
...
p = x;
q = elam*x - nu*nu/x
dqdl = x;
where
nu (standing for
) is a double global variable declared in the calling program.
Example B
The Schroedinger equation
where
over some interval ‘approximating to
’, say
. Here we need break-points at
, forming three sub-intervals
,
,
. The code could be
function [p, q, dqdl] = coeffn(x, elam, jint)
...
p = 1;
dqdl = 1;
if (jint == 2)
q = elam + x*x - 10
else
q = elam + 6/abs(x)
end
The array
xpoint would contain the values
,
,
,
,
,
and
would be
. The choice of appropriate values for
and
depends on the form of the asymptotic formula computed by
bdyval and the technique is discussed in
Examples of Boundary Conditions at Singular Points.
Example C
Here
is nearly constant over the range except for a sharp inverted spike over approximately
. There is a danger that the function will build up to a large step size and ‘step over’ the spike without noticing it. By using break-points – say at
– one can restrict the step size near the spike without impairing the efficiency elsewhere.
The code for
coeffn could be
function [p, q, dqdl] = coeffn(x, elam, jint)
...
p = 1;
dqdl = 1 - 2*exp(-100*x*x);
q = elam * dqdl;
xpoint might contain
,
,
,
,
,
(assuming
are regular points) and
would be
.
, for
, might contain
,
and
.
Examples of Boundary Conditions at Singular Points
Quoting from page 243 of
Bailey (1966): ‘Usually ... the differential equation has two essentially different types of solution near a singular point, and the boundary condition there merely serves to distinguish one kind from the other. This is the case in all the standard examples of mathematical physics.’
In most cases the behaviour of the ratio
near the point is quite different for the two types of solution. Essentially what you provide through the
bdyval is an approximation to this ratio, valid as
tends to the singular point (SP).
You must decide (a) how accurate to make this approximation or asymptotic formula, for example how many terms of a series to use, and (b) where to place the boundary matching point (BMP) at which the numerical solution of the differential equation takes over from the asymptotic formula. Taking the BMP closer to the SP will generally improve the accuracy of the asymptotic formula, but will make the computation more expensive as the Pruefer differential equations generally become progressively more ill-behaved as the SP is approached. You are strongly recommended to experiment with placing the BMPs. In many singular problems quite crude asymptotic formulae will do. To help you avoid needlessly accurate formulae,
nag_ode_sl2_breaks_funs (d02ke) outputs two ‘sensitivity coefficients’
which estimate how much the errors at the BMPs affect the computed eigenvalue. They are described in detail in
The Sensitivity Parameters and .
Example of coding bdyval: The example below illustrates typical situations:
the boundary conditions being that
should remain bounded as
tends to
and
tends to
.
At the end
there is one solution that behaves like
and another that behaves like
. For the first of these solutions
is asymptotically
while for the second it is asymptotically
. Thus the desired ratio is specified by setting
At the end
the equation behaves like Airy's equation shifted through
, i.e., like
where
, so again there are two types of solution. The solution we require behaves as
and the other as
Hence, the desired solution has
so that we could set
and
. The complete function might thus be
function [yl, yr] = bdyval(xl, xr, elam)
yl(1) = xl;
yl(2) = 2;
yr(1) = 1;
yr(2) = -sqrt(xr-elam);
Clearly for this problem it is essential that any value given by
nag_ode_sl2_breaks_funs (d02ke) to
xr is well to the right of the value of
elam, so that you must vary the right-hand BMP with the eigenvalue index
. One would expect
to be near the
th zero of the Airy function
, so there is no problem estimating
elam.
More accurate asymptotic formulae are easily found: near
by the standard Frobenius method, and near
by using standard asymptotics for
,
, (see page 448 of
Abramowitz and Stegun (1972)).
For example, by the Frobenius method the solution near
has the expansion
with
This yields
The Sensitivity Parameters σl and σr
The sensitivity parameters
,
(held in
and
on output) estimate the effect of errors in the boundary conditions. For sufficiently small errors
,
in
and
respectively, the relations
are satisfied, where the subscripts
,
denote errors committed at the left- and right-hand BMPs respectively, and
denotes the consequent error in the computed eigenvalue.
‘Missed Zeros’
This is a pitfall to beware of at a singular point. If the BMP is chosen so far from the SP that a zero of the desired eigenfunction lies in between them, then the function will fail to ‘notice’ this zero. Since the index of
of an eigenvalue is the number of zeros of its eigenfunction, the result will be that
| (a) |
the wrong eigenvalue will be computed for the given index – in fact some will be found where ; |
| (b) |
the same index can cause convergence to any of several eigenvalues depending on the initial values of elam and delam. |
It is up to you to take suitable precautions – for instance by varying the position of the BMPs in the light of knowledge of the asymptotic behaviour of the eigenfunction at different eigenvalues.
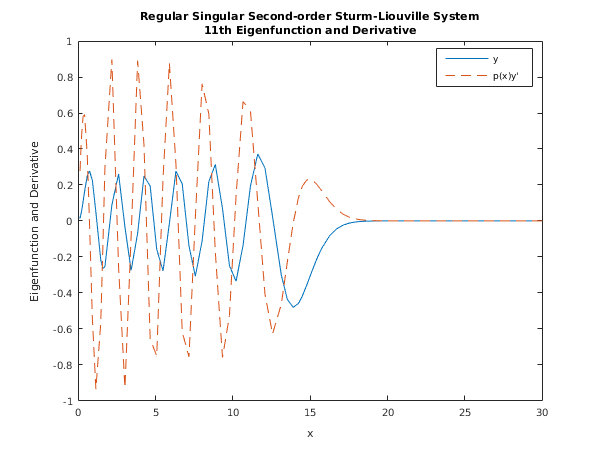
Example
This example finds the 11th eigenvalue and eigenfunction of the example of
Examples of Boundary Conditions at Singular Points, using the simple asymptotic formulae for the boundary conditions.
Comparison of the results from this example program with the corresponding results from
nag_ode_sl2_breaks_vals (d02kd) example program shows that similar output is produced from
monit, followed by the eigenfunction values from
report, and then a further line of information from
monit (corresponding to the integration to find the eigenfunction). Final information is printed within the example program exactly as with
nag_ode_sl2_breaks_vals (d02kd).
Note the discrepancy at the matching point (, the maximum of , in this case) between the solutions obtained by integrations from left- and right-hand end points.
Open in the MATLAB editor:
d02ke_example
function d02ke_example
fprintf('d02ke example results\n\n');
global ykeep ncall xkeep pkeep;
xpoint = [0; 0.1; 4d0^(1d0/3d0); 30; 30];
match = 0;
k = 11;
tol = 1d-4;
elam = 14;
delam = 1;
m = 5;
hmax = zeros(2,m);
ncall = 0;
ykeep = zeros(1,1);
xkeep = zeros(1,1);
pkeep = zeros(1,1);
[match, elam, delam, hmax, maxit, ifail] = ...
d02ke( ...
xpoint, int64(match), @coeffn, @bdyval, ...
int64(k), tol, elam, delam, hmax, 'd02kay', @report);
fprintf('\n\n');
fprintf('Eigenvalue number, k = %d\n',k);
fprintf(' estimated value = %6.3f\n',elam);
fprintf(' estimated error = %9.2e\n',delam);
fprintf(' sensitivity to left boundary = %6.3f\n',hmax(1,m-1));
fprintf(' sensitivity to right boundary = %6.3f\n\n', hmax(1,m));
fig1 = figure;
display_plot(xkeep,pkeep,ykeep)
function [yl, yr] = bdyval(xl, xr, elam)
yl(1) = xl;
yl(2) = 2;
yl(3) = 0;
yr(1) = 1;
yr(2) = -sqrt(xr-elam);
yr(3) = 0;
function [p, q, dqdl] = coeffn(x, elam, jint)
p = 1;
dqdl = 1;
q = elam - x - 2/x/x;
function report(x, v, jint)
global ykeep ncall xkeep pkeep;
if (jint == 0)
fprintf('\n A singular problem\n');
end
sqrtb = sqrt(v(1));
if (0.5*v(3) >= log(x02am))
r = exp(0.5*v(3));
else
r = 0d0;
end
pyp = r*sqrtb*cos(0.5*v(2));
y = r/sqrtb*sin(0.5*v(2));
ncall = ncall+1;
ykeep(ncall,1) = y;
xkeep(ncall,1) = x;
pkeep(ncall,1) = pyp;
function display_plot(xkeep, pkeep, ykeep)
n = length(xkeep);
for i = 2:n
if (xkeep(i-1) > xkeep(i))
x1 = [xkeep(i-1:n);rot90(xkeep(1:i-2)')];
p1 = [pkeep(i-1:n);rot90(pkeep(1:i-2)')];
y1 = [ykeep(i-1:n);rot90(ykeep(1:i-2)')];
break
end
end
plot(x1,y1,'-',x1,p1,'--');
title({'Regular Singular Second-order Sturm-Liouville System',...
'11th Eigenfunction and Derivative'});
xlabel('x'); ylabel('Eigenfunction and Derivative');
legend('y','p(x)y''','Location','Best');
d02ke example results
A singular problem
Eigenvalue number, k = 11
estimated value = 14.946
estimated error = 9.60e-04
sensitivity to left boundary = -0.015
sensitivity to right boundary = 0.000
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015