PDF version (NAG web site
, 64-bit version, 64-bit version)
NAG Toolbox: nag_quad_md_adapt_multi (d01ea)
Purpose
nag_quad_md_adapt_multi (d01ea) computes approximations to the integrals of a vector of similar functions, each defined over the same multidimensional hyper-rectangular region. The function uses an adaptive subdivision strategy, and also computes absolute error estimates.
Syntax
[
mincls,
wrkstr,
finest,
absest,
ifail] = d01ea(
a,
b,
mincls,
maxcls,
nfun,
funsub,
absreq,
relreq,
wrkstr, 'ndim',
ndim, 'lenwrk',
lenwrk)
[
mincls,
wrkstr,
finest,
absest,
ifail] = nag_quad_md_adapt_multi(
a,
b,
mincls,
maxcls,
nfun,
funsub,
absreq,
relreq,
wrkstr, 'ndim',
ndim, 'lenwrk',
lenwrk)
Description
nag_quad_md_adapt_multi (d01ea) uses a globally adaptive method based on the algorithm described by
van Dooren and de Ridder (1976) and
Genz and Malik (1980). It is implemented for integrals in the form:
where
, for
.
Upon entry, unless
mincls has been set to a value less than or equal to
,
nag_quad_md_adapt_multi (d01ea) divides the integration region into a number of subregions with randomly selected volumes. Inside each subregion the integrals and their errors are estimated. The initial number of subregions is chosen to be as large as possible without using more than
mincls calls to
funsub. The results are stored in a partially ordered list (a heap). The function then proceeds in stages. At each stage the subregion with the largest error (measured using the maximum norm) is halved along the coordinate axis where the integrands have largest absolute fourth differences. The basic rule is applied to each half of this subregion and the results are stored in the list. The results from the two halves are used to update the global integral and error estimates (
finest and
absest) and the function continues unless
where the norm
is the maximum norm, or further subdivision would use more than
maxcls calls to
funsub. If at some stage there is insufficient working storage to keep the results for the next subdivision, the function switches to a less efficient mode; only if this mode of operation breaks down is insufficient storage reported.
References
Genz A C and Malik A A (1980) An adaptive algorithm for numerical integration over an N-dimensional rectangular region J. Comput. Appl. Math. 6 295–302
van Dooren P and de Ridder L (1976) An adaptive algorithm for numerical integration over an N-dimensional cube J. Comput. Appl. Math. 2 207–217
Parameters
Compulsory Input Parameters
- 1:
– double array
-
The lower limits of integration,
, for .
- 2:
– double array
-
The upper limits of integration,
, for .
- 3:
– int64int32nag_int scalar
-
Must be set either to the minimum number of
funsub calls to be allowed, in which case
or to a negative value. In this case, the function continues the calculation started in a previous call with the same integrands and integration limits: no arguments other than
mincls,
maxcls,
absreq,
relreq or
ifail must be changed between the calls.
- 4:
– int64int32nag_int scalar
-
The maximum number of
funsub calls to be allowed. In the continuation case this is the number of new
funsub calls to be allowed.
Constraints:
- ;
- ;
- .
- 5:
– int64int32nag_int scalar
-
, the number of integrands.
Constraint:
.
- 6:
– function handle or string containing name of m-file
-
funsub must evaluate the integrands
at a given point.
[f] = funsub(ndim, z, nfun)
Input Parameters
- 1:
– int64int32nag_int scalar
-
, the number of dimensions of the integrals.
- 2:
– double array
-
The coordinates of the point at which the integrands must be evaluated.
- 3:
– int64int32nag_int scalar
-
, the number of integrands.
Output Parameters
- 1:
– double array
-
The value of the th integrand at the given point.
- 7:
– double scalar
-
The absolute accuracy required by you.
Constraint:
.
- 8:
– double scalar
-
The relative accuracy required by you.
Constraint:
.
- 9:
– double array
-
If
,
wrkstr must be unchanged from the previous call of
nag_quad_md_adapt_multi (d01ea).
Optional Input Parameters
- 1:
– int64int32nag_int scalar
-
Default:
the dimension of the arrays
a,
b. (An error is raised if these dimensions are not equal.)
, the number of dimensions of the integrals.
Constraint:
.
- 2:
– int64int32nag_int scalar
Suggested value:
, where
is the value of
maxcls and
is defined under
maxcls. If
lenwrk is significantly smaller than this, the function will not work as efficiently and may even fail.
Default:
the dimension of the array
wrkstr.
The dimension of the array
wrkstr.
Constraint:
.
Output Parameters
- 1:
– int64int32nag_int scalar
-
Gives the number of
funsub calls actually used by
nag_quad_md_adapt_multi (d01ea). For the continuation case (
on entry) this is the number of new
funsub calls on the current call to
nag_quad_md_adapt_multi (d01ea).
- 2:
– double array
-
Contains information about the current subdivision which could be used in a continuation call.
- 3:
– double array
-
specifies the best estimate obtained from the th integral, for .
- 4:
– double array
-
specifies the estimated absolute accuracy of , for .
- 5:
– int64int32nag_int scalar
unless the function detects an error (see
Error Indicators and Warnings).
Error Indicators and Warnings
Errors or warnings detected by the function:
Cases prefixed with W are classified as warnings and
do not generate an error of type NAG:error_n. See nag_issue_warnings.
- W
-
maxcls was too small for
nag_quad_md_adapt_multi (d01ea) to obtain the required accuracy. The arrays
finest and
absest respectively contain current estimates for the integrals and errors.
- W
-
lenwrk is too small for the function to continue. The arrays
finest and
absest respectively contain current estimates for the integrals and errors.
- W
-
On a continuation call,
maxcls was set too small to make any progress. Increase
maxcls before calling
nag_quad_md_adapt_multi (d01ea) again.
-
-
| On entry, | , |
| or | , |
| or | , |
| or | (see maxcls), |
| or | , |
| or | , |
| or | . |
-
An unexpected error has been triggered by this routine. Please
contact
NAG.
-
Your licence key may have expired or may not have been installed correctly.
-
Dynamic memory allocation failed.
Accuracy
An absolute error estimate for each integrand is output in the array
absest. The function exits with
if
Further Comments
Usually the running time for
nag_quad_md_adapt_multi (d01ea) will be dominated by the time in
funsub, so the maximum time that could be used by
nag_quad_md_adapt_multi (d01ea) will be proportional to
maxcls multiplied by the cost of a call to
funsub.
On a normal call, you should set on entry.
For some integrands, particularly those that are poorly behaved in a small part of the integration region,
nag_quad_md_adapt_multi (d01ea) may terminate prematurely with values of
absest that are significantly smaller than the actual absolute errors. This behaviour should be suspected if the returned value of
mincls is small relative to the expected difficulty of the integrals. When this occurs
nag_quad_md_adapt_multi (d01ea) should be called again, but with an entry value of
, (see specification of
maxcls) and the results compared with those from the previous call.
If the function is called with
, the exact values of
finest and
absest on return will depend (within statistical limits) on the sequence of random numbers generated internally within
nag_quad_md_adapt_multi (d01ea) by calls to
nag_rand_dist_uniform01 (g05sa). Separate runs will produce identical answers unless the part of the program executed prior to calling
nag_quad_md_adapt_multi (d01ea) also calls (directly or indirectly) functions from
Chapter G05, and, in addition, the series of such calls differs between runs.
Because of moderate instability in the application of the basic integration rule, approximately the last decimal digits may be inaccurate when using nag_quad_md_adapt_multi (d01ea) for large values of .
Example
This example computes
where
,
. The program is intended to show how to exploit the continuation facility provided with
nag_quad_md_adapt_multi (d01ea): the function exits with
(printing an explanatory error message) and is re-entered with
maxcls reset to a larger value. The program can be used with any values of
ndim and
nfun, except that the expression for
must be changed if
(see specification of
maxcls).
Open in the MATLAB editor:
d01ea_example
function d01ea_example
fprintf('d01ea example results\n\n');
nfun = int64(10);
ndim = 4;
absreq = 0;
relreq = 1e-3;
mincls = int64(0);
ircls = 2^ndim+2*ndim*ndim+2*ndim+1;
maxcls = int64(ircls);
lenwrk = 6*ndim+9*nfun+(ndim+nfun+2)*(1+maxcls/ircls);
ncall = 1;
a = zeros(1, ndim);
b = ones(1, ndim);
wrkstr = zeros(lenwrk, 1);
mkeep = zeros(1,1);
fkeep = zeros(1,1);
akeep = zeros(1,1);
if (ndim < 10)
mulfac = 2^ndim;
else
mulfac = 2*(ndim^3);
end
wstat = warning();
warning('OFF');
ifail = int64(1);
while (ifail == 1 || ifail == 3)
[mincls, wrkstr, finest, absest, ifail] = ...
d01ea(a, b, mincls, maxcls, nfun, @f, absreq, relreq, wrkstr);
if ifail ~= 0
fprintf('maxcls = %7d mincls = %7d ifail = %d \n\n', maxcls, ...
mincls, ifail);
else
fprintf('Success: %7d user function calls in last call\n\n', mincls);
end
fkeep(1:nfun,ncall) = finest(1:nfun);
akeep(1:nfun,ncall) = absest(1:nfun);
mkeep(ncall,1) = mincls;
mincls = int64(-1);
maxcls = maxcls * mulfac;
ncall = ncall + 1;
if ifail ~= 0
fprintf(' .. increasing maxcls to %7d\n\n', maxcls);
end
end
warning(wstat);
fig1 = figure;
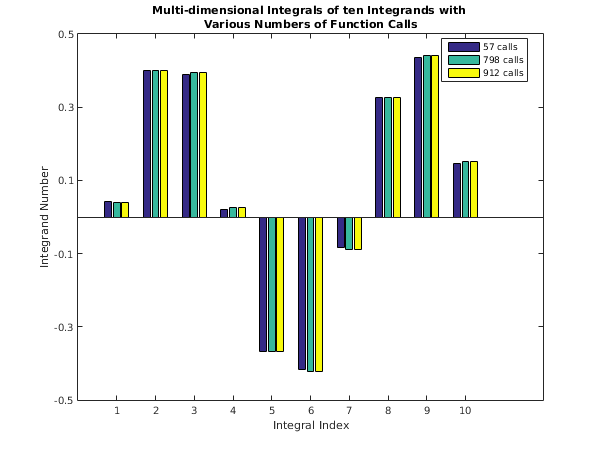
display_plot(fkeep, mkeep, 'Integrand Number');
fig2 = figure;
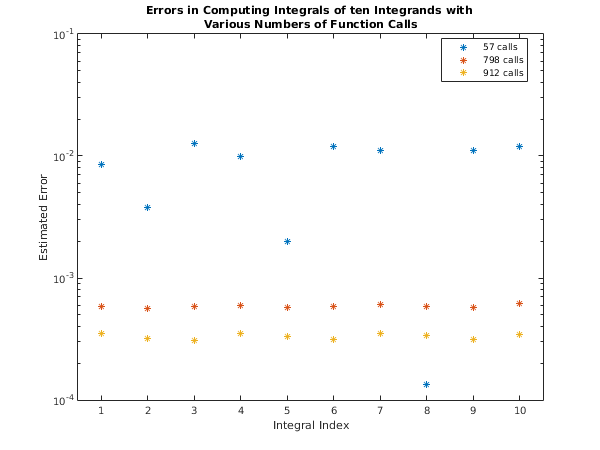
display_plot(akeep, mkeep, 'Estimated Error');
function f = f(ndim, z, nfun)
f = zeros(nfun,1);
sm = 0;
for n=1:ndim
sm = sm + double(n)*z(n);
end
for k=1:nfun
f(k) = log(sm)*sin(double(k)+sm);
end
function display_plot(data, labels, ylabelString)
if strncmp(ylabelString, 'Integrand', 9)
bar(data,'group');
title({'Multi-dimensional Integrals of ten Integrands with ', ...
'Various Numbers of Function Calls'});
set(gca, 'YTick', [-0.5 -0.3 -0.1 0.1 0.3 0.5]);
else
plot(data,'*');
title({'Errors in Computing Integrals of ten Integrands with ', ...
'Various Numbers of Function Calls'});
set(gca, 'YScale', 'log');
set(gca, 'XLim', [0.5 10.5]);
end
xlabel('Integral Index');
ylabel(ylabelString);
legend([num2str(labels(1)) ' calls'], ...
[num2str(labels(2)) ' calls'], ...
[num2str(labels(3)) ' calls'], 'Location', 'Best')
d01ea example results
maxcls = 57 mincls = 57 ifail = 1
.. increasing maxcls to 912
maxcls = 912 mincls = 798 ifail = 1
.. increasing maxcls to 14592
Success: 912 user function calls in last call
PDF version (NAG web site
, 64-bit version, 64-bit version)
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015