hide long namesshow long names
hide short namesshow short names
Integer type:  int32  int64  nag_int  show int32  show int32  show int64  show int64  show nag_int  show nag_int
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox

NAG Toolbox: nag_sum_invlaplace_crump (c06la)

▸▿ Contents

    1  Purpose
    2  Syntax
    3  Description
    4  References
▸▿ 5  Parameters
    6  Error Indicators and Warnings
    7  Accuracy
▸▿ 8  Further Comments
    9  Example

Purpose

nag_sum_invlaplace_crump (c06la) estimates values of the inverse Laplace transform of a given function using a Fourier series approximation. Real and imaginary parts of the function, and a bound on the exponential order of the inverse, are required.

Syntax

[valinv, errest, nterms, na, alow, ahigh, nfeval, ifail] = c06la(fun, t, relerr, alphab, 'n', n, 'tfac', tfac, 'mxterm', mxterm)
[valinv, errest, nterms, na, alow, ahigh, nfeval, ifail] = nag_sum_invlaplace_crump(fun, t, relerr, alphab, 'n', n, 'tfac', tfac, 'mxterm', mxterm)

Description

Given a function Fp  defined for complex values of p, nag_sum_invlaplace_crump (c06la) estimates values of its inverse Laplace transform by Crump's method (see Crump (1976)). (For a definition of the Laplace transform and its inverse, see the C06 Chapter Introduction.)
Crump's method applies the epsilon algorithm (see Wynn (1956)) to the summation in Durbin's Fourier series approximation (see Durbin (1974))
f tj ≃ e atj τ 12 F a - ∑ k=1 ∞ Re F a + kπi τ cos⁡ kπtj τ - Im F a + kπi τ sin⁡ kπtj τ ,  
for j=1,2,…,n , by choosing a such that a prescribed relative error should be achieved. The method is modified slightly if t=0.0  so that an estimate of f0.0  can be obtained when it has a finite value. τ is calculated as tfac × max0.01,tj , where tfac > 0.5 . You specify tfac  and αb , an upper bound on the exponential order α of the inverse function ft . α has two alternative interpretations:
(i) α is the smallest number such that
ft ≤ m × expαt  
for large t,
(ii) α is the real part of the singularity of Fp  with largest real part.
The method depends critically on the value of α. See Further Comments for further details. The function calculates at least two different values of the argument a, such that a>αb , in an attempt to achieve the requested relative error and provide error estimates. The values of tj , for j=1,2,…,n, must be supplied in monotonically increasing order. The function calculates the values of the inverse function ftj  in decreasing order of j.

References

Crump K S (1976) Numerical inversion of Laplace transforms using a Fourier series approximation J. Assoc. Comput. Mach. 23 89–96
Durbin F (1974) Numerical inversion of Laplace transforms: An efficient improvement to Dubner and Abate's method Comput. J. 17 371–376
Wynn P (1956) On a device for computing the emSn transformation Math. Tables Aids Comput. 10 91–96

Parameters

Compulsory Input Parameters

1:     fun – function handle or string containing name of m-file
fun must evaluate the real and imaginary parts of the function Fp for a given value of p.
[fr, fi] = fun(pr, pi)

Input Parameters

1:     pr – double scalar
2:     pi – double scalar
The real and imaginary parts of the argument p.

Output Parameters

1:     fr – double scalar
2:     fi – double scalar
The real and imaginary parts of the value Fp.
2:     tn – double array
Each tj must specify a point at which the inverse Laplace transform is required , for j=1,2,…,n.
Constraint: 0.0 ≤ t1 < t2 <⋯< tn.
3:     relerr – double scalar
The required relative error in the values of the inverse Laplace transform. If the absolute value of the inverse is less than relerr, then absolute accuracy is used instead. relerr must be in the range 0.0≤relerr<1.0. If relerr is set too small or to 0.0, then the function uses a value sufficiently larger than machine precision.
4:     alphab – double scalar
αb, an upper bound for α (see Description). Usually, αb should be specified equal to, or slightly larger than, the value of α. If αb < α then the prescribed accuracy may not be achieved or completely incorrect results may be obtained. If αb is too large nag_sum_invlaplace_crump (c06la) will be inefficient and convergence may not be achieved.
Note:  it is as important to specify αb correctly as it is to specify the correct function for inversion.

Optional Input Parameters

1:     n – int64int32nag_int scalar
Default: the dimension of the array t.
n, the number of points at which the value of the inverse Laplace transform is required.
Constraint: n≥1.
2:     tfac – double scalar
Default: 0.8
tfac, a factor to be used in calculating the parameter τ. Larger values (e.g., 5.0) may be specified for difficult problems, but these may require very large values of mxterm.
Constraint: tfac>0.5.
3:     mxterm – int64int32nag_int scalar
Suggested value: mxterm≥100, except for very simple problems.
Default: 100
The maximum number of (complex) terms to be used in the evaluation of the Fourier series.
Constraint: mxterm≥1.

Output Parameters

1:     valinvn – double array
An estimate of the value of the inverse Laplace transform at t=tj, for j=1,2,…,n.
2:     errestn – double array
An estimate of the error in valinvj. This is usually an estimate of relative error but, if valinvj<relerr, errestj estimates the absolute error. errestj is unreliable when valinvj is small but slightly greater than relerr.
3:     nterms – int64int32nag_int scalar
The number of (complex) terms actually used.
4:     na – int64int32nag_int scalar
The number of values of a used by the function. See Further Comments.
5:     alow – double scalar
The smallest value of a used in the algorithm. This may be used for checking the value of alphab- see Further Comments.
6:     ahigh – double scalar
The largest value of a used in the algorithm. This may be used for checking the value of alphab- see Further Comments.
7:     nfeval – int64int32nag_int scalar
The number of calls to fun made by the function.
8:     ifail – int64int32nag_int scalar
ifail=0 unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Note: nag_sum_invlaplace_crump (c06la) may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the function:

Cases prefixed with W are classified as warnings and do not generate an error of type NAG:error_n. See nag_issue_warnings.

   ifail=1
On entry,n<1,
ormxterm<1,
or relerr<0.0 ,
or relerr≥1.0 ,
or tfac≤0.5 .
   ifail=2
On entry, t1<0.0 ,
or t1 , t2 ,…, tn  are not in strictly increasing order.
   ifail=3
tn  is too large for this value of alphab. If necessary, scale the problem as described in Further Comments.
   ifail=4
The required accuracy cannot be obtained. It is possible that alphab is less than α. Alternatively, the problem may be especially difficult. Try increasing tfac, alphab or both.
   ifail=5
Convergence failure in the epsilon algorithm. Some values of valinvj  may be calculated to the desired accuracy; this may be determined by examining the values of errestj . Try reducing the range of t or increasing mxterm. If ifail=5 still results, try reducing tfac.
W  ifail=6
All values of valinvj  have been calculated but not all are to the requested accuracy; the values of errestj  should be examined carefully. Try reducing the range of t, or increasing tfac, alphab or both.
   ifail=-99
An unexpected error has been triggered by this routine. Please contact NAG.
   ifail=-399
Your licence key may have expired or may not have been installed correctly.
   ifail=-999
Dynamic memory allocation failed.

Accuracy

The error estimates are often very close to the true error but, because the error control depends on an asymptotic formula, the required error may not always be met. There are two principal causes of this: Gibbs' phenomena, and zero or small values of the inverse Laplace transform.
Gibbs' phenomena (see the C06 Chapter Introduction) are exhibited near t=0.0  (due to the method) and around discontinuities in the inverse Laplace transform ft . If there is a discontinuity at t=c  then the method converges such that f c → fc- + fc+ / 2 .
Apparent loss of accuracy, when ft  is small, may not be serious. Crump's method keeps control of relative error so that good approximations to small function values may appear to be very inaccurate. If ft  is estimated to be less than relerr then this function switches to absolute error estimation. However, when ft  is slightly larger than relerr the relative error estimates are likely to cause ifail=6. If this is found inconvenient it can sometimes be avoided by adding k/p  to the function Fp , which shifts the inverse to k+ft .
Loss of accuracy may also occur for highly oscillatory functions.
More serious loss of accuracy can occur if α is unknown and is incorrectly estimated. See Further Comments.

Further Comments

Timing

The value of n is less important in general than the value of nterms. Unless fun is very inexpensive to compute, the timing is proportional to na×nterms . For simple problems na=2  but in difficult problems na may be somewhat larger.

Precautions

You are referred to the C06 Chapter Introduction for advice on simplifying problems with particular difficulties, e.g., where the inverse is known to be a step function.
The method does not work well for large values of t when α is positive. It is advisable, especially if ifail=3 is obtained, to scale the problem if α  is much greater than 1.0. See the C06 Chapter Introduction.
The range of values of t specified for a particular call should not be greater than about 10 units. This is because the method uses arguments based on the value tn  and these tend to be less appropriate as t becomes smaller. However, as the timing of the function is not especially dependent on n, it is usually far more efficient to evaluate the inverse for ranges of t than to make separate calls to the function for each value of t.
The most important argument to specify correctly is alphab, an upper bound for α. If, on entry, alphab is sufficiently smaller than α then completely incorrect results will be obtained with ifail=0. Unless α is known theoretically it is strongly advised that you should test any estimated value used. This may be done by specifying a single value of t (i.e tn , n=1 ) with two sets of suitable values of tfac, relerr and mxterm, and examining the resulting values of alow and ahigh. The value of t1  should be chosen very carefully and the following points should be borne in mind:
(i) t1  should be small but not too close to 0.0 because of Gibbs' phenomenon (see Accuracy),
(ii) the larger the value of t1 , the smaller the range of values of a that will be used in the algorithm,
(iii) t1  should ideally not be chosen such that ft1=0.0  or a very small value. For suitable problems t1  might be chosen as, say, 0.1 or 1.0 depending on these factors. The function calculates alow from the formula
alow = alphab - ln0.1×relerr 2×τ .  
Additional values of a are computed by adding 1/τ  to the previous value. As τ = tfac × tn , it will be seen that large values of tfac and relerr will test for a close to alphab. Small values of tfac and relerr will test for a large. If the result of both tests is ifail=0, with comparable values for the inverse, then this gives some credibility to the chosen value of alphab. You should note that this test could be more computationally expensive than the calculation of the inverse itself. The example program (see Example) illustrates how such a test may be performed.

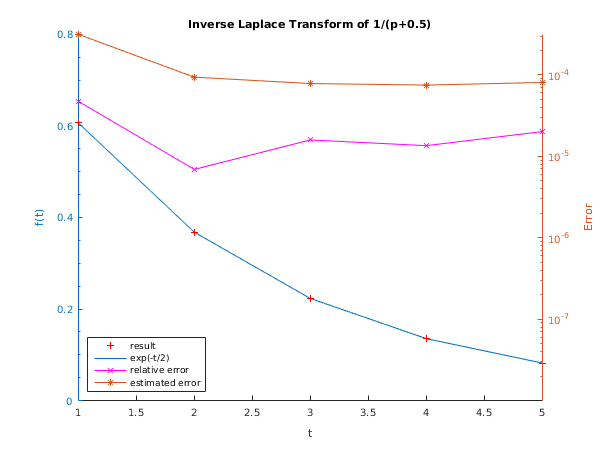
Example

This example estimates the inverse Laplace transform of the function Fp=1/p+1/2 . The true inverse of Fp  is exp-t/2 . Two preliminary calls to the function are made to verify that the chosen value of alphab is suitable. For these tests the single value t1=1.0  is used. To test values of a close to alphab, the values tfac=5.0  and relerr=0.01  are chosen. To test larger a, the values tfac=0.8  and relerr=1.0e−3  are used. Because the values of the computed inverse are similar and ifail=0 in each case, these tests show that there is unlikely to be a singularity of Fp  in the region -0.04 ≤ Rep ≤ 6.51 .

Open in the MATLAB editor: c06la_example

function c06la_example


fprintf('c06la example results\n\n');

% Initialize variables and arrays.
mxterm = int64(200);
alphab = -0.5;
n = 1;
trures = zeros(1, n);
trurel = zeros(1, n);

% First, make two preliminary calls to the routine to verify that the
% chosen alphab value is suitable.  Use t = 1 for these calls.
t(1) = 1;
disp(['Test with t(1) = ',num2str(t(1))]);

% Parameter values for a close to alphab.
tfac = 7.5;
relerr = 1e-2;
fprintf(['\nmxterm = %3.0f   tfac = %3.2f   alphab = %3.2f ', ...
         'relerr = %3.0e \n\n'], mxterm,tfac,alphab,relerr);

[valinv, errest, nterms, na, alow, ahigh, nfeval, ifail] = ...
c06la( ...
       @fun, t, relerr, alphab, 'tfac', tfac, 'mxterm',mxterm);

% Calculate results and output them.
trures(1) = exp(double(-t(1)/2));
trurel(1) = abs((valinv(1)-trures(1))/trures(1));
disp('t     Result     exp(t/2)   Relative error   Error estimate')
fprintf('%1.1f   %8.4f    %8.4f      %8.4f         %8.4f\n',...
        t(1), valinv(1), trures(1), trurel(1), errest(1));
fprintf(['\nnterms = %3d   nfeval = %3d   alow = %3.2f ', ...
         'ahigh = %3.2f   ifail = %3d\n\n'], nterms, nfeval, alow, ...
        ahigh, ifail);

% Parameter values for larger a.
tfac = 0.8;
relerr = 1e-3;
disp(['Test with t(1) = ',num2str(t(1))]);
fprintf(['\nmxterm = %3d   tfac = %3.2f   alphab = %3.2f ', ...
         'relerr = %3.0e \n\n'], mxterm, tfac, alphab, relerr);

[valinv, errest, nterms, na, alow, ahigh, nfeval, ifail] = ...
c06la( ...
       @fun, t, relerr, alphab, 'tfac', tfac, 'mxterm',mxterm);

% Calculate results and output them.
trures(1) = exp(double(-t(1)/2));
trurel(1) = abs((valinv(1)-trures(1))/trures(1));
disp('t     Result     exp(t/2)   Relative error   Error estimate')
fprintf('%1.1f   %8.4f    %8.4f      %8.5f         %8.5f\n',...
        t(1), valinv(1), trures(1), trurel(1), errest(1));
fprintf(['\nnterms = %3d   nfeval = %3d   alow = %3.2f ', ...
         'ahigh = %3.2f   ifail = %3d\n\n'], nterms, nfeval, alow, ...
        ahigh, ifail);

% Now calculate the inverse Laplace transform for several t values.
n = 5;
t = [1:5];
disp('Compute inverse')
fprintf(['\nmxterm = %3d   tfac = %3.2f   alphab = %3.2f ', ...
         'relerr = %3.0e \n\n'], mxterm, tfac, alphab, relerr);

[valinv, errest, nterms, na, alow, ahigh, nfeval, ifail] = ...
c06la( ...
       @fun, t, relerr, alphab, 'tfac', tfac, 'mxterm',mxterm);

% Calculate results and output them.
disp('t    Result    exp(t/2)   Relative error  Error estimate')
for i = 1:n
  trures(i) = exp(-t(i)/2);
  trurel(i) = abs((valinv(i)-trures(i))/trures(i));
  fprintf('%1.0f   ',t(i));
  fprintf(' %4.3f      %4.3f      %4.3e      %4.3e\n',...
          valinv(i),trures(i),trurel(i),errest(i));
end
fprintf(['\nmxterm = %3d   tfac = %3.2f   alphab = %3.2f ', ...
         'relerr = %3.0e \n\n'], mxterm, tfac, alphab, relerr);

% Plot results.
fig1 = figure;
display_plot(t,trures,valinv,trurel,errest);


function [fr,fi] = fun(preal,pimag)
  % Evaluate the real & imaginary parts of the user function.
  z = complex(1)/complex(preal+0.5,pimag);
  fr = real(z);
  fi = imag(z);

function display_plot(t, trures, valinv, trurel, errest)
  % Use a log plot for the second curve.
  [haxes, hline1, hline2] = plotyy(t, valinv, t, trurel, 'plot', 'semilogy');
  % Add the third curve (as points).
  hold on
  hpoints = plot(t, trures, '+', 'MarkerEdgeColor', 'r');
  % Set the axis limits and the tick specifications to beautify the plot.
  set(haxes(1), 'YLim', [0 0.8]);
  set(haxes(1), 'YMinorTick', 'on');
  set(haxes(1), 'YTick', [0.0 0.2 0.4 0.6 0.8]);
  set(haxes(2), 'YLim', [1e-7 5e-3]);
  set(haxes(2), 'YMinorTick', 'on');
  set(haxes(2), 'YTick', [1e-7 1e-6 1e-5 1e-4]);
  for iaxis = 1:2
    % These properties must be the same for both sets of axes.
    set(haxes(iaxis), 'XLim', [1 5]);
    set(haxes(iaxis), 'XTick', [1 1.5 2 2.5 3 3.5 4 4.5 5]);
  end
  set(gca, 'box', 'off'); % no ticks on opposite axes.
  % Add title.
  title('Inverse Laplace Transform of 1/(p+0.5)');
  % Label the x axis.
  xlabel('t');
  % Label the left and right y axes.
  ylabel(haxes(1),'f(t)');
  set(haxes(2),'YLim',[1e-8 Inf]);
  ylabel(haxes(2),'Error');
  % Add the fourth curve (plotted against the log axis).
  axes(haxes(2));
  hold on;
  hline3 = semilogy(t, errest);
  % Set some features of the three lines.
  set(hline1, 'Linewidth', 0.5, 'MarkerFaceColor', 'auto');
  set(hline2, 'Linewidth', 0.5, 'Marker', 'x', 'Color','Magenta');
  set(hline3, 'Linewidth', 0.5, 'Marker', '*', 'MarkerFaceColor', 'auto');
  % Add legend.
  legend([hpoints hline1 hline2 hline3], 'result', 'exp(-t/2)', ...
    'relative error', 'estimated error', 'Location','SouthWest');

c06la example results

Test with t(1) = 1

mxterm = 200   tfac = 7.50   alphab = -0.50 relerr = 1e-02 

t     Result     exp(t/2)   Relative error   Error estimate
1.0     0.6071      0.6065        0.0010           0.0037

nterms =  18   nfeval =  36   alow = -0.04 ahigh = 0.09   ifail =   0

Test with t(1) = 1

mxterm = 200   tfac = 0.80   alphab = -0.50 relerr = 1e-03 

t     Result     exp(t/2)   Relative error   Error estimate
1.0     0.6065      0.6065       0.00002          0.00008

nterms =  13   nfeval =  28   alow = 5.26 ahigh = 6.51   ifail =   0

Compute inverse

mxterm = 200   tfac = 0.80   alphab = -0.50 relerr = 1e-03 

t    Result    exp(t/2)   Relative error  Error estimate
1    0.607      0.607      4.746e-05      3.155e-04
2    0.368      0.368      6.910e-06      9.386e-05
3    0.223      0.223      1.589e-05      7.839e-05
4    0.135      0.135      1.353e-05      7.504e-05
5    0.082      0.082      2.014e-05      8.080e-05

mxterm = 200   tfac = 0.80   alphab = -0.50 relerr = 1e-03
c06la_fig1.png
PDF version (NAG web site, 64-bit version, 64-bit version)
Chapter Contents
Chapter Introduction
NAG Toolbox
© The Numerical Algorithms Group Ltd, Oxford, UK. 2009–2015