Note: the interface to this routine has changed since earlier releases of the toolbox:
| At Mark 22: |
lwork was removed from the interface |
nag_sum_accelerate (c06ba) performs Shanks' transformation on a given sequence of real values by means of the Epsilon algorithm of
Wynn (1956). A (possibly unreliable) estimate of the absolute error is also given.
The function must be called repetitively, once for each new term in the sequence.
Shanks D (1955) Nonlinear transformations of divergent and slowly convergent sequences J. Math. Phys. 34 1–42
None.
The accuracy of the absolute error estimate
abserr varies considerably with the type of sequence to which the function is applied. In general it is better when applied to oscillating sequences than to monotonic sequences where it may be a severe underestimate.
The time taken is approximately proportional to the final value of
ncall.
nag_sum_accelerate (c06ba) will induce convergence in some divergent sequences. See
Shanks (1955) for more details.
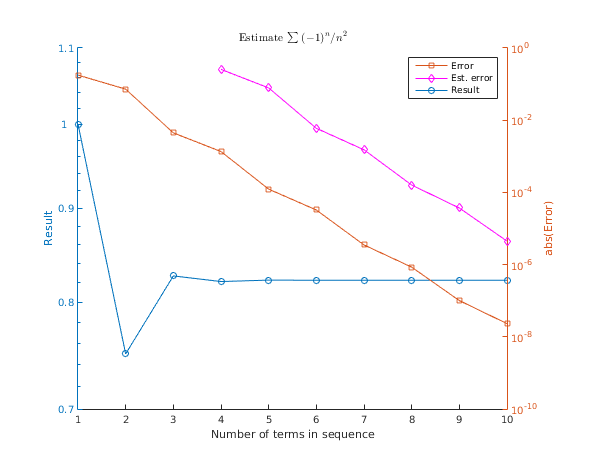
This example attempts to sum the infinite series
by considering the sequence of partial sums
function c06ba_example
fprintf('c06ba example results\n\n');
work = zeros(16, 1);
answer = pi^2/12.0;
ncall = int64(0);
sig = 1.0;
seqn = 0.0;
x = zeros(1,10);
seqnArr = zeros(1,10);
resArr = zeros(1,10);
errArr = zeros(1,10);
absArr = zeros(1,10);
disp('No. of Term Estimate Estimated Actual');
disp(' terms value of limit abs error error');
for i = 1:10;
r = double(i);
seqn = seqn + sig/(r^2);
[ncall, result, abserr, work, ifail] = ...
c06ba(seqn, ncall, work);
err = result-answer;
sig = -sig;
if i <= 3
fprintf('%4d %8.4f %8.4f - %11.2e\n', i, seqn, result, err);
else
fprintf('%4d %8.4f %8.4f %11.2e %11.2e\n', i, seqn, result, abserr, err);
end
x(i) = i;
seqnArr(i) = seqn;
resArr(i) = result;
errArr(i) = err;
if i > 3
absArr(i) = abserr;
end
end
fig1 = figure;
display_plot(x, resArr, errArr, absArr);
function display_plot(x, y1, y2, y3)
[haxes, hline1, hline2] = plotyy(x, y1, x, abs(y2), 'semilogy', 'semilogy');
set(haxes(1), 'YLim', [0.7 1.1]);
set(haxes(2), 'YLim', [1.0e-10 1]);
set(haxes(1), 'YMinorTick', 'on');
set(haxes(2), 'YMinorTick', 'on');
set(haxes(1), 'YTick', [0.7:0.1:1.1]);
set(haxes(2), 'YTick', [1.0e-10 1.0e-8 1.0e-6 1.0e-4 1.0e-2 1]);
set(haxes(1), 'YTickLabel', [0.7; 0.8; 0.9; 1.0; 1.1]);
for iaxis = 1:2
set(haxes(iaxis), 'XLim', [1 10]);
set(haxes(iaxis), 'XTick', [1:10]);
set(haxes(iaxis), 'Position',...
[0.13 0.0910780669144981 0.715317725752508 0.802973977695167]);
end
set(gca, 'box', 'off');
t1 = '{Estimate $\sum';
t2 = '{\displaystyle (-1)^n}/{\displaystyle n^2}$}';
t1 = strcat(t1,t2);
title(t1,'Interpreter','latex');
xlabel('Number of terms in sequence');
ylabel(haxes(1),'Result');
ylabel(haxes(2),'abs(Error)');
axes(haxes(2));
hold on;
hline3 = plot(x(4:10), y3(4:10));
set(hline1, 'Linewidth', 0.5, 'Marker', 'o');
set(hline2, 'Linewidth', 0.5, 'Marker', 's');
set(hline3, 'Linewidth', 0.5, 'Marker', 'd','Color','Magenta');
legend( 'Error', 'Est. error', 'Result', 'Location', 'NorthEast');