is large, sums or differences of psi functions may be computed without unnecessary loss of precision, by analytically combining the logarithmic terms. For example, the difference

d = ψ (x + \frac{1}{2}) - ψ (x)

has an asymptotic behaviour for large

x

given by

d \sim \ln (x + \frac{1}{2}) - \ln x + O (\frac{1}{x^{2}}) \sim \ln (1 + \frac{1}{2 x}) \sim \frac{1}{2 x}

Computing

d

directly would amount to subtracting two large numbers which are close to

\ln (x + \frac{1}{2})

and

\ln x

to produce a small number close to

\frac{1}{2 x}

, resulting in a loss of significant digits. However, using this function to compute

f (x) = ψ (x) - \ln x

, we can compute

d = f (x + \frac{1}{2}) - f (x) + \ln (1 + \frac{1}{2 x})

, and the dominant logarithmic term may be computed accurately from its power series when

x

is large. Thus we avoid the unnecessary loss of precision.

The function is derived from the function PSIFN in Amos (1983).

References

Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications

Amos D E (1983) Algorithm 610: A portable FORTRAN subroutine for derivatives of the psi function ACM Trans. Math. Software 9 494–502

Parameters

Compulsory Input Parameters

1: $x$ – double scalar: The argument $x$ of the function.

Constraint: $x > 0.0$ .

Optional Input Parameters

None.

Output Parameters

1: $result$ – double scalar: The result of the function.
2: $ifail$ – int64int32nag_int scalar: $ifail = 0$ unless the function detects an error (see Error Indicators and Warnings).

Error Indicators and Warnings

Errors or warnings detected by the function:

$ifail = 1$

On entry,

x \leq 0.0

. nag_specfun_polygamma (s14ac) returns the value zero.

$ifail = 2$: No result is computed because underflow is likely. The value of x is too large. nag_specfun_polygamma (s14ac) returns the value zero.

$ifail = 3$: No result is computed because overflow is likely. The value of x is too small. nag_specfun_polygamma (s14ac) returns the value zero.

$ifail = - 99$: An unexpected error has been triggered by this routine. Please contact NAG.

$ifail = - 399$: Your licence key may have expired or may not have been installed correctly.

$ifail = - 999$: Dynamic memory allocation failed.

Accuracy

All constants in nag_specfun_polygamma (s14ac) are given to approximately

18

digits of precision. Calling the number of digits of precision in the floating-point arithmetic being used

t

, then clearly the maximum number of correct digits in the results obtained is limited by

p = \min (t, 18)

With the above proviso, results returned by this function should be accurate almost to full precision, except at points close to the zero of

ψ (x)

x ≃ 1.461632

, where only absolute rather than relative accuracy can be obtained.

Further Comments

None.

Example

The example program reads values of the argument

x

from a file, evaluates the function at each value of

x

and prints the results.

Open in the MATLAB editor: s14ac_example

function s14ac_example


fprintf('s14ac example results\n\n');

x = [0.1  0.5  3.6  8];
n = size(x,2);
result = x;

for j=1:n
  [result(j), ifail] = s14ac(x(j));
end

disp('        x      Psi(x)-ln(x)');
fprintf('%12.4f%12.4f\n',[x; result]);

s14ac_plot;



function s14ac_plot
  x = [0.1:0.1:8];

  for j=1:numel(x)
    [pml(j), ifail] = s14ac(x(j));
  end

  fig1 = figure;
  plot(x,pml,'-r');
  xlabel('x');
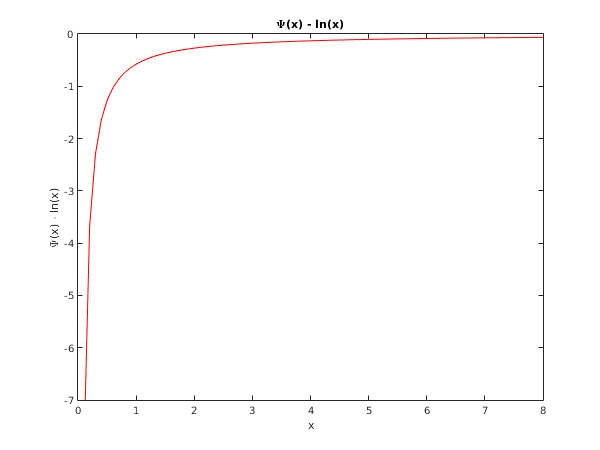
  ylabel('\Psi(x) - ln(x)');
  title('\Psi(x) - ln(x)');
  axis([0 8 -7 0]);

s14ac example results

        x      Psi(x)-ln(x)
      0.1000     -8.1212
      0.5000     -1.2704
      3.6000     -0.1453
      8.0000     -0.0638

PDF version (NAG web site, 64-bit version, 64-bit version)

Chapter Contents

Chapter Introduction

NAG Toolbox